წყაროს მიერ გამოსხივებულ სინათლეს თან მიაქვს ენერგია. სინათლის წყაროსთვის ენერგიის რესურსის მიწოდების მრავალი მექანიზმია არსებობს. იმ შემთხვევებში, როცა აუცილებელი ენერგია გათბობით გადაეცემა, ე.ი. სითბოს მიწოდებით, გამოსხივებას სითბურს ან ტემპერატურულს უწოდებენ. გამოსხივების ეს სახეობა XIX საუკუნის ფიზიკოსების განსაკუთრებულ ინტერეს იწვევდა, რადგანაც ყველა სხვა ლუმინესცენციის (ნათება) სახეობებისაგან განსხვავევით, სითბურ გამოსხივებას გახურებულ სხეულებთან შეუძლია თერმოდინამიკურ წონასწორობაში ყოფნა.
სხეულების სითბური გამოსხივების კანონზომიერებების შეაწავლისას, ფიზიკოსებს თერმოდინამიკასა და ოპტიკას შორის კავშირის დადგენის იმედი ჰქონდათ.
თუ სარკულად შემოსაზღვრულ ჩაკეტილ სიღრუეში სხვდასხვა ტემპერატურამდე გახურებულ რამოდენიმე სხეულს მოვათავსებთ, მაშინ, როგორც გამოცდილება გვიჩვენებს, ასეთი სისტემა რაღაც დროის განმავლობში სითბურ წონასწორობის მდგომარეობამდე მივა, რომლის დროსაც ყველა სხეული ერთნაერ ტემპერატურას იძენს. სხეულები ენერგიას მხოლოდ სხივური ენერგიის გამოსხივებითა და შთანთქმით ცვლიან. წონასწორობის პროცესში ყოველი სხეულის მიერ ენერგიის გამოსხივებისა და შთანთქმის პროცესები საშუალოდ აწონასწორებს ერთმანეთს და სხეულებს შორის სივრცეში ენერგიის სიმკვრივე აღწევს გარკვეულ მნიშვნელობას, რომელიც მხოლოდ დამყარებულ ტემპერატურაზეა დამოკიდებული. გარკვეული ტემპერატურის მქონე სხეულებთან თერმოდინამიკურ წონასწორობაში მყოფ ამ გამოსხივებას წონასწორულ ან შავ გამოსხივებას უწოდებენ. წონასწორული გამოსხივების სიმკვრივე და მისი სპეტრული შედგენილობა მხოლოდ ტემპერატურაზეა დამოკიდებული.
თუ მცირე ნახვრეტის საშუალებით შევიხედავთ სიღრუეში, რომელშიც გამოსხივებასა და გახურებულ სხეულებს შორი თერმოდინამიკური წონასწორობაა დამყარებული, თვალი ვერ გაარჩევს სხეულების მოყვანილობებს და დააფიქსირებს მხოლოდ მთელ სიღრუეში ერთგვაროვან ნათებას.
ვთქვათ სიღრუეში მყოფ ერთ სხეულს ახასიათებს მასზე დაცემული ნებისმიერი სპექტრული შემადგენლობის მთელი სხივური ენერგიის შთანთქმის თვისება. ასეთ სხეულს აბსოლუტურად შავს უწოდებენ. გარკვეული ტემპერატურისას გამოსხივებასთან სითბურ წონასწორობაში მყოფი აბსოლუტურად შავი სხეულის საკუთარ სითბურ გამოსხივებას იგივე სპექტრული შედგენოლობა უნდა ჰქონდეს რაც მის გარმომცველ წონასწორულ გამოსხივებას. წინააღმდეგ შემთხვევაში წონასწორობა აბსილუტურად შავ სხეულსა და მის გარემომცველ გამოსხივებას შორის ვერ დამყარდებოდა. ამიტომ ამოცანა დადის აბსოლუტურად შავი სხეულის სპექტრული გამოსხივების შესწავლასთან. კლასიკურმა ფიზიკამ ამ ამოცანის გადაწყვეტა ვერ შეძლო.
სიღრუეში წონასწორობის დამყარებისათვის აიცილებელია, რომ ყოველი სხეული მხოლოს იმდენ სხივურ ენერგიას ასხივებდეს, რამდენის შთანთქა. ეს სითბური გამოსხივების ერთ-ერთი უმნიშვნელივანესი კანონზომიერებაა. აქედან გამომდინარეომს, რომ მოცემული ტამპერატურის შემთხვევაში აბსოლუტურად შავი სხეული ზედაპირის ფართობის ერთეულიდან დროის ერთეულში ნებისმიერ სხვა სხეულზე მეტ სხივურ ენერგიას ასხივებს.

ნახ. 1.
აბსოლუტურად შავი სხეული
აბსოლუტურად შავი სხეულები ბუნებაში არ არსებობენ. ასეთი სხეულის კარგ მოდელს ჩაკეტილ სიღრუეში ნახვრეტი წარმოადგენს (ნახ. 1). ნახვრეტიდან სიღრუეში მოხვედრილი სინათლე მრავალრიცხოვანი არეკვლის შემდეგ თითქმის მთლიანად შთაინთქმება კედლების მიერ, და ნახვრეტი გარედან სრულიად შავად გამოჩნდენა. მაგრამ, თუ სიღრუე გაცხელებულია გარკვეულ T ტტმპერატურამდე, და შიგნით კი დამყარდა სითბური წონასწორობა, ნახვრეტიდან გამოსული გამოსხივება აბსოლუტურად შავი სხეულის გამოსხივება იქნება. სითბური გამოსხივების შემსწავლელ ყველა ექსპერიმენტში სწორედ ასე ხდება აბსოლუტურად შავი სხეულის მოდელირება.
სიღრუის შიგნით ტემპერატურის ზრდით ნახვრეტიდან გამოსული გამოსხივების ენერგიაც იზრდება და იცვლება სპექტრული შედგენილობა.
მოცემული T ტემპერატურისათვის აბსოლუტურად შავი სხეულის გამოსხივებაში ენერგიის ტალღის სიგრძეების მიხედვით განაწილება ხასიათდება გამოსხივების უნარით r (λ, T), რომელიც სხეულის ზედაპირის ფართობის ერთეულიდან ტალღის სიგრძეთა ერთეულ ინტერვალში გამოხსვების სიმძლავრის ტოლია. ნამრავლი r (λ, T) Δλ ერთეულოვანი ზედაპირის მიერ ყველა მიმართულებით ტალღის სიგრძეთა Δλ ინტერვალში გამოსხივების სიმძლავრის ტოლია. ანალოგიურად შეიძლება ენერგიის სიხშირეების მიხედვით განაწილების r (ν, T) შემოტანა. ფუნქციას r (λ, T) (ან r (ν, T)) ხშირად სპექტრულ ნათებას უწოდებენ, ხოლო ყველა ტალღის სიგრძის მიერ გამოსხივებულ R (T) სრულ ნაკადს, რომელიც ტოლია

ინტეგრალურ ნათებას უწოდებენ.
XIX საუკუნის ბოლოს აბსოლუტურად შავი სხეულის გამოსხივება ექსპერიმენტულად კარგად იყო შესწავლილი.
1879 წელს იოზეფ სტეფანმა ექსპერიმენტული მონაცემების ანალიზის სიფუძველზე დაასკვნა, რომ აბსოლუტურად შავი სხეულის ინტეგრალური ნათება R (T) აბსოლუტური T ტემპერატურის მეოთხე ხარისხის პროპორციულია:
R (T) = σT4.
ცოდა მოგვიანებით, 1884 წელს ბოლცმანმა ეს დამოკიდებულება თერმოდინამიკურ მოსაზრებებზე დაყრდნობით თეორიოლად გამოიყვანა. ამ კანონმა სტეფან-ბოლცმანის კანონის სახელწოდება მიიღო. σ მუდმივას რიცხვითი მნიშვნელობა, თანამედროვე გაზომვების მიხედვით, ტოლია
σ = 5,671·10–8 Вт / (м2 · К4).
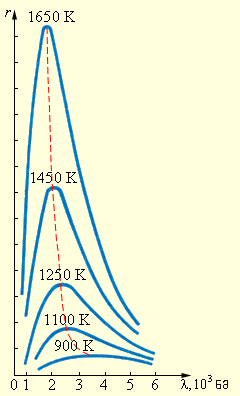
ნახ. 2.
სხვადასხვა ტემპერატურისათვის აბსოლუტურად შავი სხეულის გამოსხივების სპექტრული განაწილება r (λ, T)
XIX საუკინის 90-იან წლებში შესრულდა აბსოლუტურად შავი სხეულის გამოსხივების სპექტრული განაწილების ზედმიწევნით ფაქიზი ექსპერიმენტული გაზომვები, რომლებმაც აჩვენეს, რომ ტემპერატურის ყოველი T მნიშვნელობისთვის r (λ, T) დამოკიდებულებას მკვეთრად გამოსახული მაქსიმუმი აქვს (ნახ. 2). ტემპერატურის ზრდით მაქსიმუმი მოკლე ტალღის სიგრძეებისკენ ინაცვლებს, ამასთან მაქსიმუმის შესაბამისი ტემპერატურისა და ტალღის სირძის ნამრავლი მუმივი რჩება:
λmT = b ან λm = b / T.
ეს დამოკიდებულება ადრე ვინისვინის მიერ იყო მიღებილი თერმოდინამიკიდან. იგი ე.წ. ვინის წანაცვლების კანონს გამოსახავს: ტალღის სიგრძე λm, რომელიც აბსოლუტურად შავი სხეულის გამოსხივების მაქსიმუმი მოდის, აბსოლუტური ტემპერატურის T უკუპროპორციულია. ვინის მუდმივას მნიშვნელობაა
b = 2,898·10–3 მ·К.
ლაბორატორიულ პირობებში პრაქტულულად მიღწევადი ტემპერატურებისთვის გამოსხივების უნარის მაქსიმუმი r (λ, T) ინფრაწითელ უბანში მდებარეობს. მხილოდ როცა T ≥ 5·103 К- შსემთხვევაში მაქსიმუმი ხილულ სპექტრულ უბანში ხვდება. მზის გამოსხივების ენერგიის მაქსიმუმი დაახლოებით 470 ნმ-ზე (სპექტრის მწვანე უბანი) მოდის, რაც მზის გარე ფენის ტემპერატურას დაახლოებით 6200 К-ს შეესაბამება (თუ მზეს აბსოლუტურად შავი სხეულად განვიხილავთ).
სტეფან-ბოლცმანისა და ვინის კანონების თეორიული გზით გამოყვანაში თერმოდინამიკის წარმატებამ იმედე გააჩინა, რომ თერმოდინამიკური მოსაზრებების გამოყენებით შესაძლებელი იქნებიდა აბსოლუტურად შავი სხეულის გამოსხივების სპექტრული განაწილების ყველა მრუდის r(λ, T) მიღება. 1900 წელს ამ პრობლემის გადაჭრას ცნიბილი ინგლისელი ფიზიკოსი ჯ.რელეი ცდილობდა, რომელიც თავის მსჯელობების საფუძველად იყენებდა კლასიკური სტატისტიკის თეორემას თერმოდინამიკური წონასწორობისას ენერგიის თავისუფლების ხარისხების მიხედვით თანაბარი განაწილების შესახებ. ეს თეორემა რელეიმ სიღრუეში წონასწორული მდგომარეობის პირობებში გამოიყენა. მოგვიანებით ეს იდეა დაწვრილებით განავითარა ჯინსმა. ამგვარად გახდა შესაძლებელი აბსოლუტურად შავი სხეულის გამოსხივების უნარის ტალღის სიგრძესა λ და ტემპერატურაზე T დამოკიდებულებისმიღება:
r (λ, T) = 8πkTλ–4.
ამ თანაფარდობას რელეი-ჯინსის ფორმულას უწოდებენ. იგი ექსპერიმენტულ მონაცემებთან მხოლოს საკმარისად გრძელი ტალღებისათვისაა თანხმობაში (ნახ. 3). ამის გარდა, ამ ფორმულიდან გამოდის აბსურდული დასკვნა იმის შესახებ, რომ აბსოლუტურად შავი სხეულის ინტეგრალური ნათობა R (T) უნდა უსასრულო ხდებოდეს, ხოლო, აქედან გამომდინარე, გახურებულ სხეულსა და ჩაკეტილი სიღრუის გამოსხივებას შორის წონასწორობა შეიძლება მხოლოდ ტემპერატურის აბსოლუტური ნულის დროს დამყარდეს.

ნახ. 3.
აბსოლუტურად შავი სხეულის გამოსხივების ტალღის სიგრძეების მიხედვით ენერგიის განაწილების r (λ, T) შედარება რელეი-ჯინსის ფორმულასთან T = 1600 К-სათვის
ამგვარად, კლასიკური ფიზიკის თვალსაზრისით უნაკლო დასკვნას მივყავართ ფომულამდე, რომელიც ცდებს მკვეთრად ეწინააღმდეგება. ნათელი გახდა, რომ აბსოლუტურად შავი სხეულის გამოსხივების სპექტრული განაწილების შესახებ ამოცანის გადაჭრა არსებული თეორიის პირობებში შეუძლებელი იყო. ეს ამოცანა მ.პლანკმა წარმატებით გადაწყვიტა კლასიკური ფიზიკისათვის უცხო, ახალი იდეის დახმარებით.
პლანკი მივიდა დასკვნამდე, რომ გახურებული სხეულის მიერ ელექტრომაგნიტური ენერგიის გამოსხივებისა და შთანთქმის პროცესები უწვეტად კი არ მიმდინარეობს, რორც კლასიკურ ფიზიკაში იყო მიღებული, არამედ სასრული პორციების - ქვანტების სახით. ქვანტი სხეულის მიერ გამოსხივებული ან შთანთქმული ენერგიის მინიმალური პორციაა. პლანკის თეორიის მიხედვით ქვანტის ენერგია E სინათლის სიხშირის პირდაპირპროპორციულია:
E = hν,
სადაც h – ე.წ. პლანკის მუდმივაა. h = 6,626·10–34 ჯ·წმ. პლანკის მუდმივა უნივერასლური კონსტანტაა, რომელიც ქვანტურ ფიზიკაში იგივე როლს ასრულებს, რასაც სინათლის სიჩქარე ფარდობითობის სპეციალურ თეორიაში.
ელექტრომაგნიტური გამოსხივების გამოსხივებისა და შთანთქმის პროცესები წყვეტილი ხასიათის შესახებ ჰიპითეზის საფუძველზე პლანკმა მიიღო ფორმულა აბსოლუტურად შავი სხეულის სპექტრული ნათობისათვის. პლანკის ფორმულა მოსახერხებელია ჩაიწეროს ისეთი ფორმით, როცა აბსოლუტურად შავი სხეულის გამოსხივების ენერგიის განაწილება სპექტრში გამოსახულია სიხშირით ν, და არა ტალღის სიგრძით λ.
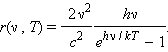
სადაც c – სინათლის სიჩქარე, h – პლანკის მუდმივა, k – ბოლცმანის მუდმივა, T – აბსოლუტური ტემპერატურაა.
პლანკის ფორმულა კარგად აღწერს აბსოლუტურად შავი სხეულის გამოსხივების სპექტრულ განაწილებას ნებისმიერი სიხშირისათვის. ის კარგ თანხმობაშია ექსპერიმენტულ მონაცემებთან. პლანკის ფორმულიდან შეიძლება სტეფან-ბოლცმანის და ვინის კანონების გამოყვანა. როცა hν << kT პლანლის ფორმულა რელეი-ჯინსის ფორმულაში გადადის.
შავი სხეულის გამოსხივების პრობლემის გადაჭრა ფიზიკაში ახალი ეპოქის დაწყებით აღინიშნა. ადვილი არ იყო კლასიკურ ფიზიკაზე უარის თქმა, თითონ პლანკიც კი, მისივე უდიდესი აღმოჩენის შემდეგაც, რამოდენიმე წლის განმავლობაში უშედეგოდ ცდილობდა ენერგიის დაქვანტვის კლასიკური ფიზიკის თვალსაზრისიდან ახსნას.


