ვთქვათ მყარი ძელაკი უძრავადაა მოთავსებული ათვლის K' სისტემაში, რომელიც სიჩქარით მოძრაობს ათვლის ისიტემის მიმართ (ნახ. 1). ძელაკი x' ღერძის პარალელურადაა ორიენტირებული. მისი სიგრძე, რომელიც K' სისტემაში ეტალონური სახაზავითაა გაზომილი, l0-ს ტოლია. მას საკუთარ სიგრძეს უწოდებენ. როგორი იქნება ამ ძეალკის K სისტემაში მყოფი დამკვირვებლის მიერ გაზომილი სიგრძე? ამ კითხვაზე პასუხის გასაცემად აუცილებელია მოძრავი ძელაკის სიგრძის გაზომვის პროცედურა განიმარტოს.
ძელაკის l სიგრძეში K სისტემაში, რომლის მიმართაც ძელაკი მოძრაობს, იგულისხმება ძელაკის ბოლოების კოორდინატებს შორის მანძილი, რომელიც ამ სისტემის საათებით ერთდროულად დაფიქსირდა. თუ ცნობილია K' სისტემის სიჩქარე K სისტემის მიმართ, მაშინ მოძრავი ძელაკის სიგრძის გაზომვა შეიძლება დროის გაზომვამდე დაიყვანოს: υ სიჩქარით მოძრავი ძელაკის l სიგრძე υτ0 ნამრავლის ტოლია, სადაც τ0 – K სისტემის საათების მიხედვით დროის ინტერვალია სისტემის რაღაც უძრავი წერტილის (მაგალითად, A წერტილის) მიმართ ძელაკის დასაწყისისა და დაბოლოების გავლებს შორის (ნახ. 1). რადგანაც K სისტემაში ორივე ხდომილება (ფიქსირებული წერტილის მიმართ ძელაკის დასაწყისისა და დაბოლოების გავლა) ხდება ერთ წერტილში, დროის τ0 შუალედი K სისტემაში საკუთარ დროს წარმოადგენს. ამგვარად, მოძრავი ძელაკის l სიგრძე ტოლია l = υτ0.
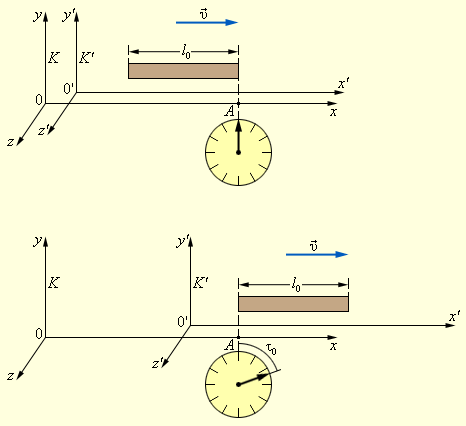
ნახ. 1.
მოძრავი ძელაკის სიგრძის გაზომვა
ახლა ვიპოვოთ კავშირი l და l0 შორის. K' სისტემის დამკვირვებლისათვის K სისტემის კუთვნილი A წერტილი უძრავი ძელაკის მიმართ მარცხნივ υ სიჩქარით, ამიტომ შეიძლება ჩაიწეროს
l0 = υτ,
სადაც τ K' სისტემის სინქრონული საათებით გაზომილი ძელაკის ბოლოებთან A წერტილის ჩავლის მომენტებს შორის დროის შუალედია. τ და τ0 დროის შუალედებს შორის კავშირის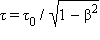 
გამოყენებით, ვიპოვით
ამგვარად, ძელაკის სიგრძე იმ ათვლის სისტემის არჩევაზეა დამოკიდებული, რომელშიც ის იზომება, ე.ი. ფარდობით სიდიდეს წარმოადგენს. ძელაკის სიგრძე უდიდესი გამოდის იმ სისტემაში, რომელშიც ძელაკი უძრავია. დამკვირვებლის მიმართ მოძრავი სხეულები თავიანთი მოძრაობის მხარეს მოკლდებიან. ამ რალატივისტურ ფაქტს სიგრძის ლორენცის დამოკლებას (შეკუმშვას) უწოდებენ.
მანძილი არ არი აბსოლუტური სიდიდე, ის მოცემილი ათვლის სისტემის მიმართ სხეულის მოძრაობის სიჩქარეზეა დამოკიდებული. სიგრძის დამოკლება არ არის დაკავშირებული სხეულში მიმდინარე რაიმე პროცესთან. ლორენცის შეკუმშვა ახასიათებს სხეულის ზომის ცვლილებას მისი მოძრაობის მიმართულებით. თუ ძელაკს ნახ. 1-ზე მოვათავსებთ x ღერძის მართობულად, რომლის მიმართაც მოძრაობს K' სისტემა, მაშინ ძელაკის სიგრძე ორივე, K და K' სისტემის დამკვირვებლისთვის ერთნაირი აღმოჩნდება. ეს მტკიცებულება თანხმობაშია ყველა ინერციული სისტემის თანაბარუფლებიანობის პოსტულატთან. დასაბუთებისთვის შემდეგი აზრობრივი ექსპერიმენტი შეიძლება განვიხილოთ. K და K' სისტემებში y და y' ღერძების გასწვრივ მოვათავსოთ ორი მყარი ძელაკი. ძელაკებს ერთნაერი საკუთარი l სიგრძეები აქვთ, რომლებიც ძელაკებისადმი უძრავი K და K' სისტემის დამკვირვებლების მიერაა გაზომილი და ორივე ძელაკის ერთ-ერთი ბოლო კოორდინატთა O ან O' სათავეს ემთხვევა. გარკვეულ მომენტში ძელაკების ერთმანეთის გვერდი-გვერდ აღმოჩნდებიან და შესაძლებელი ხდება მათი პირდაპირი შედარება: ყოველი ძელაკის ბოლოს შეუძლია აღნიშვნა გააკეთოს მეორე ძელაკზე. თუ ეს აღმიშვნები ძელაკების ბოლოებს არ დაემთხვევა, ერთ-ერთი მატგანი მეორეძე გრძელი აღმოჩნდება ორივე ათვლის სიტემის თვალსაზრისით. ეს კი ფარდობითობის პრიციპის საწინააღმდეგო ფაქტი იქნებოდა.
საყურადღებოა, რომ მოძრაობის დაბალი (υ << c) სიჩქარეებისას ფარდობითობის სპეციალური თეორიის ფორმულები კლასიკურ თანაფარდობებში გადადიან: l ≈ l0 და τ ≈ τ0. ამგვარად, ნიუტონის მექანიკის კლასიკური წარმოდგენები, რომლებიც ნელ მოძრაობებზე დაკვირვების მრავალსაუკუნოვანი ექსპერიმენტული გამოცდილების საფუძველზე ჩამოყალიბდა, ფარდობითობის სპეციალურ თეორიაში ზღვრილ β = υ / c → 0 გადასვლას შეესაბამება. ამაში მდგომარეობს შესაბამისობის პრინციპი.