XIX საუკუნის დასაწყისში, როცა თ.იუნგი და ო.ფრენელი სინათლის ტალღურ თეორიაზე მუშაობდნენ, სინათლის ტალღების ბუნება უცნობი იყო. პირველ ეტაპზე ითვლებოდა, რომ სინათლე გრძივ ტალღას წარმოადგენდა, რომელიც რაღაც ჰიპოტეტურ გარემოში - ეთერში ვრცელდებოდა. ინტერფერენციისა და დიფრაქციის მოვლენების შესწავლისას საკითხს იმის შესახებ, სინათლის ტალღები გრძივი იყო თუ განივი მეორეხარისხოვანი მნიშვნელობა ჰქონდა. იმ დროს შეუძლებლად ეჩვენებოდათ, რომ სინათლე განივი ტალღაა, მექანიკურ ტალღებთან ანალოგიიდან გამომდინარე უნდა დაეშვათ, რომ ეთერი მყარი სხეული იყო (განივ მექანიკურ ტალღებს აიროვან და თხევად გარემოში გავრცელება არ შეუძლიათ).
მაგრამ ნელ-ნელა გროვდებოდა ექსპერიმენტული ფაქტები, რომლების სინათლის განივი ტალღების სასარგებლოდ მეტყველებდნენ. ჯერ კიდევ XVII საუკუნის ბოლოში აღმოჩნდა, რომ ისლანდიური შპატის კრისტალი (CaCO3) მასში გამავალ სხივსა აორებს. ამ მოვლენას ორმაგი სხივთა გარდატეხა უწოდეს (ნახ.1).
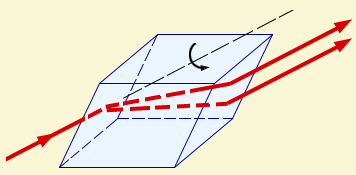
ნახ. 1.
ისლანდიური შპატის კრისტალშე სხივის გავლა (ორმაგი სხივთა გარდატეხა). თუ კრისტალს ვაბრუნებთ საწყისი სხივის მიმართ, კრისტალში გამოსული ორივე სხივი ბრუნდება
1809 წელს ფრანგმა ინჟინერბა ე.მალიუსმა აღმოაჩინა კანონი, რომელიც მის სახელს ატარებს. მალიუსის ცდებში სინათლეს ატარებნენ თურმალინის ორ ერთნაერ ფირფიტაში (მომწვანო შეფერილობის გამჭვირვალე კრისტალური ნივთიერება). ფიტფიტების ერთმანეთის მიმართ φ კუთხით მობრუნება იყო შესაძლებელი (ნახ. 2).
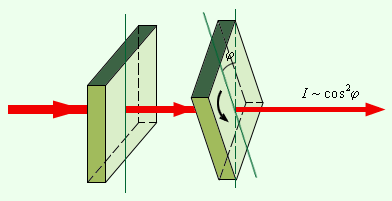
ნახ. 2.
მალიუსის კანონის ილუსტრაცია
გასული სინათლის ინტენსივობა cos2 φ-ის პირდაპირპროპორციული აღმოჩნდა:
I ~ cos2 φ.
არც ორმაგი სხივთა გარდატეხა და არც მალიუსის კანონი გრძივი ტალღების თეორიით არ იხსნებიდა. გრძივი ტალღებისათვის სხივის გავრცელების მიმართულება სიმეტრიის ღერძს წარმოსდგენს. გრძივ ტალღაში სხივის მართობულ სიბრტყეში ყველა მიმართულება თანაბარუფლებიანია. განივ ტალღაში (მაგალითად, რეზინის ზონარზე მორბენალ ტალღაში) რხევის მიმართულება და მისი მართობული მიმართულებები თანაბარი არ არის (ნახ. 3).

ნახ. 3.
რეზინის ზონარზე მორბენალი ტალღა. ნაწილაკები y ღერძის გასწვრივ ირხევიან. S ჭვრიტის მობრუნება ტალღის ჩაქრობას იწვევს
ამგვარად, გავრცელების (სხივის) მიმართულებით ასიმეტრია განივი ტალღის გრძივისაგან განმასხვავებელი ძირითადი მახასიათებელია. სინათლის ტალღების განივობის შესახებ პირველად მოსაზრება იუნგამა გამოთქვა 1816 წელს. ფრენელმა იუნგისგან დამოუკიდებლად ასევე წამოაყენა სინათლის ტალღების განივობის კონცეფცია, დაასაბუთა მრავალრიცხოვანი ექსპერიმენტებით და შექმნა კრისტალში სინათლის ორმაგი სხივთა გარდატეხის თეორია.
XIX საუკუნის 60-იან წლებში სინათლის ცნობილი სიჩქარის ელექტრომაგნიტური თალღების სივრცული გავრცელების სიჩქატესთან დამთხვევის საფუძველზე მაქსველმა დაასკვნა, რომ სინათლე ელექტომაგნიტური ტალღაა. ამ დროისათვის სინათლის ტალღების განივობა უკვე ექსპერიმენტულად იყო დასაბუთებული. ამიტომ, მაქსველი სამართლიანად თვლიდა, რომ ელექტრომაგნიტური ტალღების განივობა სინათლის ტალღების ელექტრომაგნიტური ბუნების კიდევ ერთი უმნიშვნელოვანესი დასაბუთებაა.
სინათლის ელექტრომაგნიტურმა თეორიამ მწყობრი სახე მიიღო, რამდენადაც არ იყო ტალღის გავრცელებისათვის აუცილებელი განსაკუთრებული გარემოს - ეთერის შემოღების აუცილებლობა.
ელექტრომაგნიტურ ტალღაში \(\vec{E}\) და \(\vec{B}\) ვექტორები ურთიერთმართობულია და ტალღის გავრცელების მართობულ სიბრტყეში მგებარეობენ (ნახ. 3). სინათლის ნივთიერებასთან ურთიერთქმედების ყველა პროცესში ძირითად როლს ელექტრული \(\vec{E}\) ვექტორი ასრულებს, ამიტომაც მას სინათლეს ვექტორს უწოდებენ. თუ ელექტრომაგნიტური ტალღების გავრცელებისა სინათლის ვექტორი ორიენტაციას ინარჩუნებს, ასეთ ტალღას წრფივად პოლარიზებულს უწოდებენ (ტერმინი პოლარიზაცია მალიუსის მიერ იყო შემოტანილი განივი ტალღების შესწავლისას). სიბრტყეს, რომელშიც სინათლის ვექტორი \(\vec{E}\) ირხევა, რხევის სიბრტყეს უწოდებენ (yz სიბრტყე ნახ. 2.6.3-ზე), ხოლო სიბრტყეს, რომელშიც ირხევა \(\vec{B}\) ვექტორი - პოლარიზაციის სიბრტყე ეწოდება ( xz სიბრტყე ნახ. 2.6.3-ზე).
თუ ერთიდაიგივე მიმართულების ორი მონოქრომატული ერთმანეთის მართობულ სიბრტყეებში პოლარიზებული ტალღა ვრცელდება, მათი შეკრების შემთხვევაში წარმოიქმნემა ელიფსურად პოლარიზებული ტალღა (ნახ. 4).
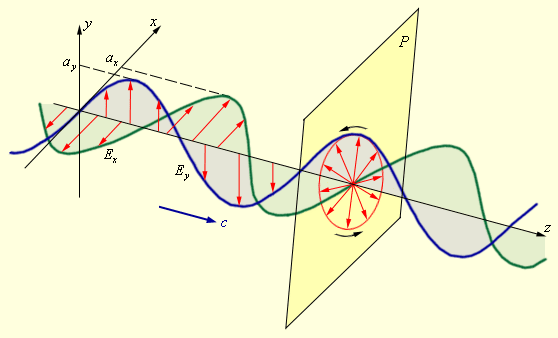
ნახ. 4.
ორი ერთმანეთის მართობულ სიბრტყეებში მდებარე პოლარიზებული ტალღის შეკრება და ელიფსურად პოლარიზებული ტალღის წარმოქმნა
ელიფსურად პოლარიზებული ტალღის ნებისმიერ, ტალღის გავრცელების მართობულ სიბრთყეში ჯამური ვექტორის ბოლო სინათლის რხევის ერთი პერიოდის განმავლობაში ერთ ელიფსს შემოსწერს, რომელსაც ელიფსურ პოლარიზაციას უწოდებენ. ელიფსის ფორმა და ზომები წრფივად პოლარიზებული ტალღების ax და ay ამპლიტუდებითა და მათ შორის ფაზათა სხვაობით განისაზღვრება. ელეიფსური პოლარიზაციის კერძო შემთხვევას წრიული პოლარიზაცია წარმოადგრნს (ax = ay, Δφ = ± π / 2).
ნახ. 5 ელიფსურად პოლარიზებული ტალღების სივრცულ სტუქტურაზე იძლევა წარმოდგენას.
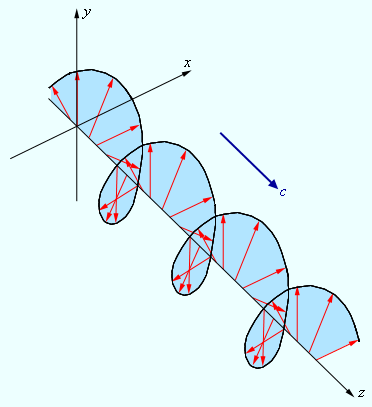
ნახ. 5.
ელიფსირად პოლარიზებული ტალღის ელიფსური ველი
წრფივად პოლარიზებულ სინათლეს ლაზერული წყარო იძლევა. სინათლე პოლარიზებული შეიძლება აღმოჩნდეს არეკვლის ან გაბნების შემთხვევაში. კერძოდ, ცისფერი სინათლე ცაზე ნაწილობრივ ან სრულად პოლარიზებულია. მაგრამ, ჩვეულებრივი წყაროების სინათლე (მაგალითად, მზის სინათლე, ვარვარების ნათურის სხივი და ა.შ.) პოლარიზებული არ არის. ასეთი წყაროების სინათლე ყოველ მომენტში შედგება აურაცხელი რაოდენობის, დამოუკიდებალად გამომსხივებადი, ატომების წვლილისაგან, რომელთა მიერ გამოსხივებული ტალღების სინათლის ვექტორები სხვდასხვანიერადაა ორიენტირებული. ამიტომაც ჯამური ტალღის \(\vec{E}\) ვექტორის ორიენტაცია დროში უწესრიგოს იცვლება, საშუალოდ რხევის ყველა მიმართულება თანაბარუფლებიანი აღმოჩნდება. პოლარიზაციის არ მქონე სინათლეს ბუნებრივ სინათლეს უწოდებენ.
დროის ყოველ მომენტში \(\vec{E}\) ვექტორი შეიძლება დაგეგმილდეს ორ ურთიერთმართობულ ღერძზე (ნახ. 6).
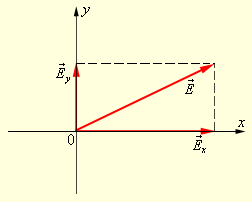
ნახ. 6.
\(\vec{E}\) ვექტორის ღერძებზე დაშლა
ეს ნიშნავს, რომ ნებისმიერი ტალღა (პოლარიზებული და პოლარიზაციის არ მქონე) შეიძლება წარმოვიდგინოთ ორი ურთიერთმართობული მიმართულებით, წრფივად პოლარიზებული ტალღა: \(\vec{E(t)}=\vec{E_{x}(t)}+\vec{E_{y}(t)}\). მაგრამ, პოლარიზებულ ტალღაში ორივე Ex (t) და Ey (t) მდგენელი კოჰერენტულია, ხოლო არაპოლარიზებულის დროს - არაკოჰერენტული, ე.ი. პირველ შემთხვევაში Ex (t) და Ey (t) შორის ფაზათა სხვაობა მუმივია, ხოლო მეორეში ის დროის შემთხვევით ფუნქციას წარმოადგენს.
სინათლის ორმაგი სხივთაგარდატეხა იმით აიხსნება, რომ მრავალ კრისტალურ ნივთიერებაში ურთიერთმართობული მიმართულებით წრფივად პოლარიზებული ტალღების გარდატეხის კოეფიციენტი განსხვავებულია. ამიტომაც კრისტალი მასში გამავალ სინათლეს ორ ნაწილად ყოფს (ნახ. 1). გამოსასვლელზე ორი სხივი წრფივად პოლარიზებული ურთიერთმართობული მიმართულებით. კრისტალებს, როლმებშიც ორმაგ ხსივტაგარდატეხა ხდება, ანიზოტროპულებს უწოდებენ.
\(\vec{E}\) ვექტორის ღერძებზე დაგეგმილების საშუალებით შიძლება აიხსნას მალიუსის კანონი (ნახ. 2).
მრავალი კრისტალისათვის სინათლის შთანთქმა ძლიერადაა დამოკიდებული სინათლის ტალღის ელექტრული ვექტორის მიმართულებაზე. ამ მოვლენას დიქროიზმს უწოდებენ. ეს თვისება, ნაწილობრივ, მალიუსის ცდებში გამოყენებულ თურმალინის ფირფიტასაც ახასიათებს. გარკვეული სისქისას თურმალინის ფირფიტა თითქმის სრულად შთანთქავს ურთიერთპერპენდიკულარულად პოლარიზებული ტალღებიდან ერთ-ერთს (მაგალითად,Ex) და ნაწილობრივ ატარებს მეორე ტალღას (Ey). გასული სხივის ელექტრული ვექტორის რხევის მიმართულებას ფირფიტის დაშვებულ მიმართულებას უწოდებენ. თურმალინის ფირფიტა შეიძლება გამოყენებული იქნეს, როგორც პოლარიზებული სინათლის მისაღებად (პოლარიზატორი), ასევე სინათლის პოლარიზაციის ხასიათის ანალიზისათვის (ანალიზატორი). დღეისათვის ფართოდ იყენებენ ხელოვნურ დიქროიდულ აპკებს, რომლებსაც პოლაროიდებს უწოდებენ. პოლაროიდები დაშვებული პოლარიზაციის ტალღას თითქმის სრულად ატარებენ ხოლო მართობული მიმართულებით ოილარიზებულ ტალღას არ ატარებენ. ამგვარად, პოლაროედები შეიძლება იდეალურ პოლარიზაციულ ფილტრებად ჩაითვალონ.
განვიხილოთ ბუნებრივი სინათლის მიმდევრობითი გავლა ორ იდეალურ П1 და П2 პოლაროიდში (ნახ. 7), რომელთა დაშვებული მიმართულებები ერთმანეთის მიმართ გარკვეული φ კუთხითაა მიმართული. პირველი პოლაროიდი პოლარიზატორის როლს ასრულებს. ის ბუნებრივ სინათლეს წრფივად პოლარიზებულად გარდაქმნის. მეორე პოლარიზატორი მასაძე დაცემული სინათლის ანალიზისთვის გამოიყენება.

ნახ. 7.
ბუნებრივი სინათლის ორ იდეალურ პოლაროიდში გავლა. yy' – პოლაროიდის დაშვებული მიმართულებაა.
თუ პირველ პოლაროიდში გავლის შემდეგ წრფივად პოლარიზებული ტალღის ამპლიტიდას 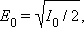 -ით ავღნიშნავთ, მაშინ მეორე პოლარიზატორის მიერ გატარებული ტალღის ამპლიტუდა E = E0 cos φ. აქედან გამომდინარე, მეორე პოლარიზატორიდან გამოსვლილას წრფივად პოლარიზებული ტალღის ინტენსივობა I ტოლია
-ით ავღნიშნავთ, მაშინ მეორე პოლარიზატორის მიერ გატარებული ტალღის ამპლიტუდა E = E0 cos φ. აქედან გამომდინარე, მეორე პოლარიზატორიდან გამოსვლილას წრფივად პოლარიზებული ტალღის ინტენსივობა I ტოლია
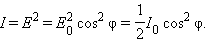
ამგვარად, მალიუსის კანონი 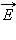 ვექტორის გეგმილებად დაშლის საფუძველზე ბუნებრივ ახსნას პოულობს ელექტრომაგნიტურ თეორიაში.
ვექტორის გეგმილებად დაშლის საფუძველზე ბუნებრივ ახსნას პოულობს ელექტრომაგნიტურ თეორიაში.


