სინათლის დიფრაქციას წინააღმდეგობის მახლობლად გავლისას სინათლის სხივის წრფივი გავრცელების მიმართულებიდან გადახრის მოვლენას უწოდებენ. როგორ გამოცდილებიდანაა ცნობილი, გარკვეულ პირობებში სინათლეს შეუძლია გეომეტრული ჩრდილის არეში სეშვლა. თუ სინათლის პარალელური კონის გზაზე მრგვალი წინაღობაა მითავსებული (მრგვალი დისკო, ბურთულა ან გაუმჭვივალე ეკრანზე მრგვალი ხვრელი), მაშინ წინააღმდეგობიდან საკმარისად დიდ მანძილზე მოთავსებულ ეკრანზე გამოჩნდება დიფრაქციული სურათი - ნათელი და ბნელი რგოლების მონაცვლეოვა. თუ წინააღმდეგობას წრფივი ხასიათი აქვს (ჭვრიტე, ძაფი, ეკრანის კიდე), მაშინ ეკრანზე გამოჩნდება პარალელური დიფრაქციული ზოლები.
დიფრაქციული მოვლენები ჯერ კიდებ ნიუტონის დროს კარგად იყო ცნობილი, მაგრამ კორპუსკულური თეორიის საფუძველძე მათი ახსნა შეუძლებელი აღმოჩნდა. ამ მოვლენის პირველი თვისობრივი ახსნა ტალღური წარმოდგენების საუძველზე თ.იუნგის მიერ იქნა წარმოდგენილი. მისგან დამოუკიდებლად 1818 წელს ფრანგმა მეცნიერმა ო.ფრენელმა განავითარა დიფრაქციული მოვლევების რაოდენობრივი თეორია. თეორიას საფუძვლად ფრენელმა ჰიუგენსის პრინციპი დაუდო, რომელიც მეორადი ტალღების ინტერფერენციის იდეით შეავსო. ჰიუგენსის პრინციპმა, პირველსაწყისი სახით მხოლოდ ტალღური ფრონტების დროის ყოველ შემდგომი მდებარეობების პოვნის საშუალება მისცა, ე.ი. ტალღის გავრცელების მიმართულების დადგენისა. არსებითად, ეს გეომეტრული ოპტიკის პრინციპია. ჰიუგენსის ჰიპოთეზა, მეორადი ტალღების ფრონტის შესახებ ფრენელმა ფიზიკურად გასაგები პოზიციით შეცვალა, რომლის მიხედვითაც, მეორადი ტალღები დაკვირვების წერტილში გავლისას ერთმანეთთან ინტერფერირებენ. ჰიუგენს-ფრენელის პრინციპი გარკვეულ ჰიპოთეზას წარმოადგენდა, მაგრამ შემდგომმა გამოცდილებამ მისი სამართლიანობა დაადასტურა. ნახ. 1-ზე ჰიუგენს-ფრენელის პრინციპის ილუსტრაციაა მოცემული.
ნახ. 1.
ჰიუგენს-ფრენელის პრინციპი. ΔS1 და ΔS2 – ტალღური ფრონტის ელემენტებია, 
и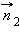 
– ნორმალები
ვთქვათ S ზედაპირი გარკვეულ მომენტში ტალღის ფრონტს წარმოადგენს. ტალღურ თეორიაში ტალღის ფრონტს უწოდებენ ზედაპირს, რომლის ყოველ წერტილშიც რხევა ფაზის ერთიდაიგივე სიდიდით მიმდინარეობს (სინფაზა). კერძოდ, ბრტყელი ტალღის ტალღის ფრონტი ტალღის გავრცელების მიმართულების მართობულ პარალელურ სიბრტყეთა ოჯახია. წერტილოვანი წყაროს მიერ გამოსხივებული სფერული ტალღის ტალღის ფრონტები კონცენტრულ სფეროთა ოჯახია.
რაიმე P წერტილში ტალღით გამოწვეული რხევა რომ განისაზღვროს, ფრენელის მიხედვით საჭიროა ჯერ განისაზღვროს რხევა გამოწვეული ამ წერტილში გარკვეული მეორადი ტალღებით, რომლებიც ამ წერტილში ყველა ელემენტარული ზედაპირიდან S (ΔS1, ΔS2 და ა.შ.) იყრის თავს, და შემდეგ ეს რხევები უნდა შეიკრიბოს მათი ამპლიტუდებისა და ფაზების გათვალისწინებით. ამასთან, გათვალისწინებული უნდა იყოს მხოლოდ ის ელემენტარული ზედაპირები S, რომლებსაც რაიმე სახის წინაღობა ხვდებათ.
მაგალითისათვის განვიხილოთ უბრალო დიფრაქციული ამოცანა დაშორებული წყაროდან მომავალი ბრტყელი მონოქრომატული ტალღის მიერ გაუმჭვირვალე ეკრანში მცირე R რადიუსის მქონე ხვრელის გავლა (ნახ. 2).
ნახ. 2.
ეკრანში მრგვალი ხვრელის ირგვლივ წარმოქმნილი დიფრაქციული ბრტყელი ტალღები
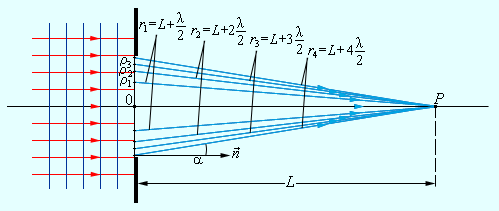
დაკვირვების P წერტილი სიმეტრიის ღერძზე მდებარეობს ეკრანიდან L მანძილზე. ჰიუგენს-ფრენელის პრინციპის შესაბამისად ტალღური ზედაპირი აზრობრივად ხვრელის სიბრტყესთან თანხვედრილი, მეორადი წყაროებით დასახლებულად უნდა წარმოვიდგინოთ, რომელთაგან ტალღები აღწევენ P წერტილს. მეორადი ტალღების ინტერფერენციის შედეგად P წერტილში გარკვეული ჯამური რხევა წარმოიქმნება, რომლის ამპლიტუდის კვადრატი (ინტენსივობა) უნდა განისაზღვროს დაცემული ტალღის λ ტალღის სიგრძის, A0 ამპლიტუდის წინასწარ მოცემული მნიშვნელობების და ამოცანის გეომეტრიიდან გამომდინარე. გათვლების გასაიოლებლად ფრენელმა წინააღმდეგობის განლაგების ადგილას დაცემული ტალღის ტალღური ზედაპირი დაყო რგოლოვან ზონებად (ფრენელის ზონები) შემდეგი წესით: მეზობელი ზონის საზღვრებიდან P წერტილამდე მანძილი ერთმანეთისაგან ტალღის სიგრძის ნახევრით უნდა განსხვავდებოდნენ, ე.ი.
ტალღის ზედაპირს P წერტილიდან ყურების შემთხვევაში, ფრენელის ზონის საზღვარები კონცენტრულ წრეებს უნდა წარმოადგენდნენ (ნახ. 3).
ნახ. 3.
ხვრელის სიბრტყეში ფრენელის ზონების საზღვრები
ნახ 3-დან ადვილია ფრენელის ზონების ρm რადიუსების პოვნა:
რადგან ოპტიკაში λ << L, ფესვქვეშ მეორე წევრი შეიძლება უგულვებელვყოთ. ფრენელის ზონების რაოდენობა, რომლებიც ხვრელზე თავსდება, მისი R რადიუსით განისაზღვრება:
აქ არ არის აუცილებელი m მთელი რიცხვი იყოს. P წერტილში მეორადი ტალღების ინტერფერენციის შედეგი ფრენელის ღია ზონების m რიცხვბზეა დამოკიდებული. ადვილი საჩვენებელია, რომ ყველა ზონას თანაბარი ფართობი აქვს:
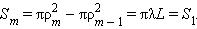
ფართობით ერთნაერი ზონები დაკვირვების წერტილში ერთნაერი ამპლიტუდის რხევებისგან უნდა აღიძვრებოდეს. მაგრამ ყოველი მომდევნო ზონისთვის დაკვირვების წერტილში გავცელებულ სხივსა და ტალღის ზედაპის შორის კუთხე α იზრდება. ფრენელი გამოთქვამდა მოსაზრებას (ექსპერიმენტით განმტკიცებულს), რომ კუთხის გადიდებით რხევის ამპლიტუდა, უმნიშვნელოდ, მაგრამ მაინც მცირდება:
A1 > A2 > A3 > ... > A1
სადაც Am – m-ური ზონით გამოწვეული რხევის ამპლიტუდაა.
კარგ მიახლოებად შეიძლება ჩაითვალოს, რომ ზოგიერთი ზონით გამოწვეული რხევის ამპლიტუდა ორი მეზობელი ზონით გამოწვეული რხევების ამპლიტუდების საშუალო არითმეტიკულის ტოლია, ე.ი.
რადგანაც ორი მეზობელი ზონის დაკვივების წერტილამდე მანძილები ერთმანეთისაგან λ / 2-ით განსხვევდება, ამიტომ, ამ ზონების გამომწვევი რხევები საწინააღმდეგი ფაზებში იმყოფებიან. ამიტომ ორი მეზობელი ზონიდან ტალღა თითქმის აქრობენ ერთმანეთს. დაკვივების წერტილში ჯამური ამპლიტუდა ტოლია
A = A1 – A2 + A3 – A4 + ... = A1 – (A2 – A3) – (A4 – A5) – ... < A1.
ამგვარად, P წერტილში ჯამური რხევის ამპლიტუდა ყოველთვის ნაკლებია რხევის ამპლიტუდაზე, რომელსაც ერთი პირველი ზონა შექმნიდა. კერძოდ, ფრენელის ყველა ზონა რომ ღია იყოს, მაშინ დაკვირვების წერტილში მიაღწევდა წინააღმდეგობით შეუშფოთებელი ტალღა A0 ამპლიტუდით. ამ დროს შეიძლება ჩაიწეროს:
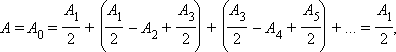
რადგანაც ბრჩხილებში მოთავსებული გამოსახულება ნულის ტოლია. აქედან გამომდინარე, მთელი ტალღური ფრონტის მიერ გამოწვეული მოქმედება (ამპლიტუდა), ერთი ზონის მოქმედების ნახევრის ტოლია.
ამგვარად, თუ გაუმჭვირვალე ეკრანის ხვრელი ღიად ტოვებს ფრენელის მხოლოდ ერთ ზონას, მაშინ დაკვირვების წერტილში რხევის ამპლიტუდა 2-ჯერ იზრდება (ინტენსივობა - 4-ჯერ) აღუშფოთებელ ტალღასთან შედარებით. თუ ღიაა ორი ზონა. რხევის ამპლიტუდა ნულის ტოლი ხდება. თუ არ დავამზადებთ გაუმჭვირვალე ეკრანს, რომელიც ღიად დატოვებს მხოლოდ რამდენიმე კენტ (ან მხოლოს ლუწ) ~ ზონას, მაშინ რხევის ამპლიტუდა გაიზრდება. მაგალითად, თუ ღიაა 1, 3 და 5 ზონები, მაშინ
A = 6A0, I = 36I0
ისეთ ფირფიტებს, რომლებსაც გააჩნიათ სინათლის ფოკუსირების თვისება ზონალურ ფირფიტებს უწოდებენ.
მრგვალ დიკზე სინათლის დიფრაქციისას დახურული არმოჩნდება 1-დან m-მდე ფრენელის ზონა. როცა დაკვირვების წერტილში რხევების ამპლიტუდები ტოლი იქნება
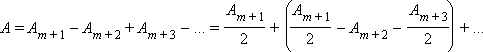
ან A = Am + 1 / 2, რადგანაც, ბრჩხილებში მდგომი გამოსახულება ნულის ტოლია. დისკი ხურავს საკმაოდ დიდი ნომრის მქონე ზონას, მაშინ Am + 1 ≈ 2A0 და A ≈ A0, ე.ი. სურათის ცენტრში სინათლის დიფრაქციისას დისკზე დაიკვირვება ინტერფერენციის მაქსიმუმი. ეს ე. წ. პუასონის ლაქაა, ის ნათელი და ბნელი დიფრაქციული რგოლებითაა გარშემორტყმული.
შევაფასოთ ფრენელის ზონის ზომები. ვთქვათ, მაგალითად, წინააღმდეგობიდან L = 1 მ მანძილზე მოთავსებულ ეკრანზე დაიკვირვება დიფრაქციული სურათი. ტალღის სიგრძე λ = 600 ნმ (წითელი სინათლე). ფრენელის პირველი ზონის რადიუსი ტოლია
ამგვარად, ოპტიკურ დიაპაზონში ტალღის სიგრძეების სიმცირის გამო ფრენელის ზონების ზომები საკმარისად მცერე აღმოჩნდება. დიფრაქციული მოვლენები ყველზე მკაფიოდ ვლინდება, როცა წინააღმდეგობა ზონების მხოლოდ ძალიან მცირე რიცხვს ფარავს:
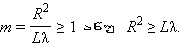
ეს თანაფარდობა შეიძლება განვიხილოთ როგორც დიფრაქციის დაკვირვების კრიტერიუმი. თუ ფრენელის ზონების რიცხვი, რომელსაც წინააღმდეგობა ფარავს, ძალიან დიდი ხდება, დიფრაქციის მოვლენა პრაქტიკულად შეუმჩნეველია:
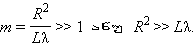
ეს ძლიერი უტოლობა გეომეტრული ოპტიკის გამოყენების საზღვარს განსაზღვრავს. სინათლის ვიწრო კონა, რომელსაც გეომეტრულ ოპტიკაში სხივს უწოდებენ, მხოლოდ ამ პირობების შესრულების შემთხვევაში ფორმირდება. ამგვარად, გეომეტრული ოპტიკა ტალღური ოპტიკის ზღვრულ შემთხვევას წარმოადგენს.
ზევით განხილული იყო დაშორებული წყაროდან მრგვალი ფორმის წინააღმდეგობაზე სინათლის დიფრაქციის შემთხვევა. თუ სინათლის წერტილოვანი წყარო სასრულ მანძილზე მდებარეობას, მაშინ წინააღმდეგობაზე ეცემა სფერულად განშლადი ტალღა. ამ შემთხვევაში ამოცანის გეომეტრია რამდენადმე რთულდება, რამდენადაც ახლა ფრენელის ზონები უნდა აიგოს არა ბრტყელ, არამედ სფერულ ზედაპირზე (ნახ. 4).
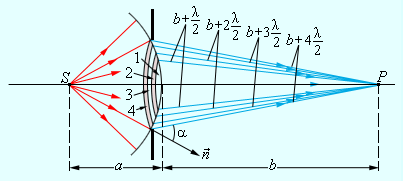
ნახ. 4.
ტალღის სფერული ფრონტის ფრენელის ზონები
ტალღის სფერულ ფრონტზე ფრენელის ზონების ρm რადიუსების გათვლებს შემდეგ გამოსახულებამდე მივყავართ:
ფრენელის თეორიის ზემოთ მოყვანილი დასკვნები ამ შემთხვევაშიც სამართლიანია.
უნდა აღინიშნოს, რომ სინათლის ტალღების დიფრაქციის (და ინტერფერენციის) თეორიის გამოყენება ნებისმიერი ფიზიკური ბუნების ტალღებისთვისაა შესაძლებელი. ამაში ვლინდება ტალღური კანონზომიერებების ერთიანობა. XIX საუკუნის დასაწყისში, როცა იუნგი, ფრენელი და სხვა მეცნიერები ტალღუს თეორიას ქმნიდნენ სინათლის ფიზიკური ბუნება ჯერ კიდევ არ იყო ცნობილი.