გეომეტრული ოპტიკის ძირითადი კანონები სინათლის ფიზიკური ბუნების დადგენამდე გაცილებით ადრე იყო ცნობილი.
სინათლი წრფივად გავრცელების კანონი: ოპტიკურად ერთგვაროვან გარემოში სინათლე წრფივად ვრცელდება. ამ კანონის ცდისეულ დასაბუთებას მკვეთრი ჩრდილების არსებობა წარმოადგენს, რომლებსაც მცირე ზომის სინათლის წყაროს („წერტილოვანი წყარო“) მიერ განათებული გაუმჭვირვალე სხეულები იძლევიან. სხვა დასაბუთებად შეიძლება გამოვიყენოთ ცნობილი ცდა, როლის დროსაც შორეული სინათლის წყაროს სხივის მცირე ზომის ჭუჭრუტანაში გასვლის შედეგად ვიწრო სხივთა კონა წარმოიქმნება. ამ ცდას მივყავართ წარმოდგენამდე, რომ სინათლის სხივი გეომეტრული წრფეა, რომლის გასწვრივაც ვრცელდება სინათლე. უნდა აღინიშნოს, რომ სინათლის წრფივად გავრცელების კანონი ირღვევა და სინათლის სხივის ცნება აზრს კარგავს, თუ სინათლე ისეთ მცირე ზიმის ხვრელში გადის, რომლის ზომებიც შედარებადია სინათლის ტალღის სიგრძსთან. ამგვარად, გეომეტრული ოპტიკა, რომელიც სინათლის სხივზე წარმოდგენას ეყრდნობა, არის ტალღური ოპტიკის ზღვრული შემთხვევა როცა λ → 0. გეომეტრული ოპტიკის გამოყენების საზღვრები სინათლის დიფრაქციისადმი მიძღვნილ თავში იქნება განხილული.
ორი გამჭვირვალე გარემოს გამყოფ ზედაპირზე სინათლე შეიძლება ნაწილობრივ აირეკლოს, ისე რომ სინათლის ენერგიის ნაწილი არეკვლის შემდეგ გავრცელდება ახალი მიმართულებით, ხოლო ნაწილი გაივლის გამყო ზედაპორს და გააგრძელებს გავრცელებას მეორე გარემოში.
სინათლის არეკვლის კანონი: დაცემული და არეკვლილი სხივები, და ასევე ორი გარემოს გამყოფი ზედაპირის სხივის დაცემის წერტილში აღმართული მართობი ერთ სიბრტყეში მდებარეობს (დაცემის სიბრტყე). არეკვლის γ კუთხე დაცემის α კუთხის ტოლია.
სინათლის გარდატეხის კანონი: დაცემული და გარდატეხილი სხივები, და ასევე ორი გარემოს გამყოფი ზედაპირის სხივის დაცემის წერთილში აღმართული მართობი ერთ სიბრტყეში მდებარეობს. დაცემული α კუთხის სინუსის ფარდობა გარდატეხილი β კუთხის სინუსთან მოცემული ორი გარემოდსათვის მუმივი სიდიდეა:
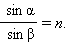
გარდატეხის კანონი ექსპერიმენტულად იქნა დადგენილი ჰოლანდიელი მეცნიერის ვ.სნელიუსის მიერ 1621 წელს.
n მუდმივ სიდედეს უწოდებენ მეორე გარემოს ფარდობით გარდატეხის მაჩვენებელს პირველის მიმართ. გარემოს გარდატეხის მაჩვენებელს ვაკუუმის მიმართ აბსოლუტურ გარდატეხის მაჩვენებელს უწოდებენ.
ორი გარემოს გარდატეხის ფარდობითი მაჩვენებელი მათი აბსოლუტური მაჩვენებლების ფარდობის ტოლია:
n = n2 / n1.
არეკვლისა და გარდატეხის კანონები ტალღური ფიზიკით აიხსნება. ტალღური წარმოდგენების თანახმად, გარდატეხა ერთი გარემოდან მეორეში გადასვლისას ტალღის გავრცელების სიჩქარის ცვლილების შედეგს წარმოადგენს. გადრატეხის მაჩვენებლის ფიზიკური არსი პირველ გარემოში ტალღის გავრცელების υ1 სიჩქარის მეორე გარემოში გარცელების υ2 სიჩქარესთან ფარდობაში მდგომარეობს:
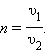
გარდატეხის აბსოლუტური მაჩვენებელი სინათლის ვაკუუმში გავრცელების c სიჩქარის გარემოში გავრცელების υ სიჩქარესთან ფარდობის ტოლია :

ნახ.1-ზე არეკვლისა და გარდატეხის კანონებია ნაჩვენები.

ნახ. 1.
არეკვლისა და გარდატეხის კანონები: γ = α;n1 sin α = n2 sin β.
ნაკლები გარდატეხის აბსოლუტური მაჩვენებლის მქონე გარემოს, ოპტიკურად ნაკლებად მკვრივს უწოდებენ.
სინათლის ოპტიკურად უფრო მკვრივი გარემოდან ნაკლებად მკვრივში გადასვლისას n2 < n1 (მაგალითად, მინიდან ჰაერში) შეიძლება სრული არეკვლის, ანუ გარდატეხილი სხივის გაქრობის, მოვლენას დავაკვირდეთ. ეს მოვლენა დაიკვირვება ისეთი დაცემის კუთხეებისათვის, რომლებიც გარკვეულ კრიტიკულ αზღ კუთხეს აჭარბებენ. ამ კუთხეს სრული შინაგანი არეკვლის ზღვრულ კუთხეს უწოდებენ (ნახ. 2).
დაცემის კუთხისთვის α = αზღ sin β = 1; sin αზღ = n2 / n1 < 1.
თუ მეორე გარემოს ჰაერი წარმოადგენს (n2 ≈ 1), მაშინ ამ ფორმილის გადაწერა შემდეგი სახითაა მოსახერხებელი
sin αზღ = 1 / n,
სადაც n = n1 > 1 – პირველი გარემოს გარდატეხის აბსოლუტური მაჩვენებელია.
მინა-ჰაერის გამყოფი ზედაპირისათვის (n = 1,5) კრიტიკული კუთხე αზღ = 42°, წყალი- ჰაერისათვის კი (n = 1,33) αზღ = 48,7°.
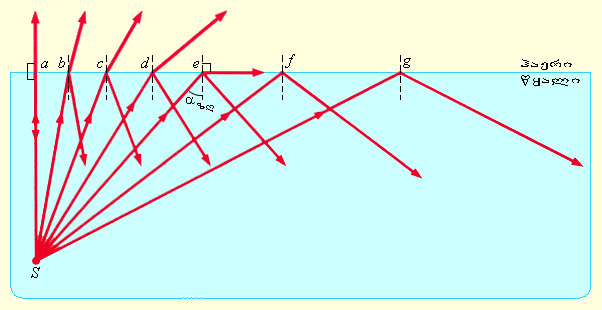
ნახ. 2.
სინათლის სრული შინაგანი არეკვლა წყლისა და ჰაერის გამყოფ ზედაპირზე; S – სინათლის წერტილოვანი წყაროა
სრული შინაგანი არეკვლის მოვლენა მრავალ ოპტიკურ ხელსაწყოში გამოიყენება. განსაკუთრებით საინტერესო და მნიშვნელოვან მაგალითი ბოჭკოვანი სინათლის გამტარების შექმნაა, რომლების ოპტიკურად გამჭვირვალე (მინა, კვარცი), წვრილ (რამოდენიმე მიკრომეტრიდან მილიმეტრამდე) მოქნილი ძაფებია. ბოჭკოვანი სინათლის გამტარების ბოლოზე მოხვედრილ სინათლე მასში, გვერდითი ზედაპირებიდან სრული შინაგანი არეკვლის ხარჯზე, შეიძლება დიდ მანძილებზე გავრცელდეს (ნახ. 3). სამეცნიერო-ტექნიკურ მიმართულებას, რომელიც ბოჭკოვანი სინათლის გამტარების შემუშავებითა და დამზადებითაა დაკავებული, ბოჭკოვანი ოპტიკა ეწოდება.
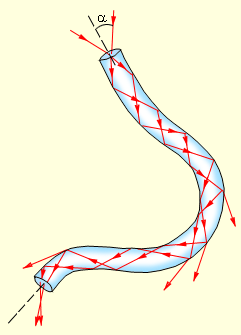
ნახ. 3.
სინათლის გავრცელება ბოჭკოვანი სინათლის გამტარში. ბიჭკოების ძლიერი გადაღუნვისას სრული შინაგანი არეკვლის კანონი ირღვევა, და სინათლე ნაწილობრივ გამოდის ბოჭკოს გვერდითი ზედაპირიდან


