რადგან რხევა იქნება მილევადი, მისი პერიოდი შეიძლება გამოვთვალოთ შემდეგი ფორმულით
\(T=\frac{2\pi }{\sqrt{\omega _{0}^{2}-\beta ^{2}}}\). (1)
სადაც ω0 - მილევის გარეშე სისტემის რხევის საკუთარი სიხშირეა. მილევის β კოეფიციენტი დაკავშირებულია Т პერიოდთან თანაფარდობით \(\beta =\frac{\lambda }{T}\) . ზამბარიანი ქანქარის საკუთარი სიხშირე არის \(\omega _{0}=\sqrt{\frac{k}{m}}\), სადაც k ზამბარის სიხისტის კოეფიციენტია. სიხისტის კოეფიციენტი შეიძლება მოიძებნოს იმ პირობიდან, რომ m მასის ტვირთის მოქმედების გამო ზამბარა გაჭიმულია Δх სიგრძით.
ტვირთის წონასწორობის პირობა ამ სახისაა kΔx = mg.
აქედან \(\frac{k}{m}=\frac{g}{\Delta x}\) .
შესაბამისად, ტვირთის საკუთარი სიხშირე იქნება
 .
.
ჩავსვათ ω0-ისა და β-ს მნიშვნელობები (1) ფორმულაში, მარტივი გარდაქმნების შედეგად მივირებთ
\(T=\sqrt{\frac{\left ( 4\pi ^{2}+\lambda ^{2} \right )\Delta x}{g}}=\)0.7წმ.
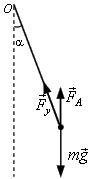
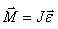
სადაც \(J\) - ქამქარის ინერციის მომენტია, M - ძალების ჯამური მომეტი, ხოლო \(\varepsilon =\frac{\mathrm{d} ^{2}\alpha }{\mathrm{d} t^{2}}\) არის კუთხური აჩქარება. რადგან დაჭიმულობის ძალის მოქმედების წრფე გადის ბრუნვის ღერძზე, მისი მომენტი ნულის ტოლია. სიმძიმის ზალის მომენტი იქნება M1 = mglsinα, არქიმედის ძალის მომენტი კი - M2 = FAlsinα . აქედან გამომდინარე მოძრაობის განტოლებას ექნება სახე
\(ml^{2}\frac{\mathrm{d} ^{2}\alpha }{\mathrm{d} t^{2}}=\left ( mg-F_{A}\right )l\sin \alpha\) . (2)
გავითვალისწინოთ, რომ m = ρV, სადაც ρ- ბურთულის მასალის სიმკვრივეა, ხოლო \(\vec{F}_{A}=-\rho _{l}V\vec{g}\)და ასევე მცირე კუთხეებისთვის sinα ≈ α, მაშინ განტოლება (2) მიიღებს სახეს:
.\(\frac{\mathrm{d} ^{2}\alpha }{\mathrm{d} t^{2}}+\frac{\left (\eta -1\right )}{l\eta }g \alpha=0\)
ეს არის ჰარმონიული რხევის განტოლება და რხევის სიხშირე არის \(\omega _{0}=\sqrt{\frac{\left (\eta -1\right )}{l\eta }g}\) .
პერიოდი იქნება \(T=\frac{2\pi }{\omega _{0}}\)
ჩავსვათ შესაბამისი რიცხვები.
ამოცანის ამოხსნისთვის მოსაახერხებელია გამოვიყენოთ რხევების წარმოდგენის გრაფიკული მეთოდი. განსახილველი რხევების მოძრაობის კანონები ჩაიწერება ასე: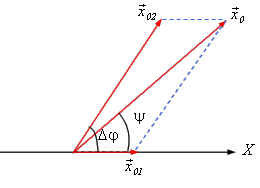
x1 = x01cosωt,
x2 = x02cos(ωt + Δφ)
სადაც x01 და x02 - არის მერხევი ნაწილაკის წანაცვლებები წონასწორობის მდგომარეობიდან. პირველი რხევითი პროცესის საწყისი ფაზა ჩათვლილია ნულად. რადგან სიხშირეები ტოლია, ამიტომ რხევების გამომსახველ ვექტორებს შორის კუთხე არ იცვლება დროში. ამიტომ ვექტორული დიაგრამა შეიძლება აიგოს t = 0 მომენტისთვის. ნახაზიდან ჩანს, რომ
x02 = x012 + x022 + 2x01x02cosΔφ.
უკანასკნელი გამოსახულება გამომდინარეობს კოსინუსების თეორემიდან. ჩავსვათ რიცხვითი მნიშვნელობები და მივიღებთ x0= 13 სმ. ჯამური რხევის საწყისი ფაზა ტოლი იქნება Х ღერძსა და ჯამური რხევის \(\vec{x}_{0}\) ვექტორს შორის ψ კუთხის. გეომეტრული მოსაზრებებიდან ჩანს, რომ
. \(tg\psi =\frac{x_{02\sin \Delta \varphi }}{x_{01}+x_{02}\cos \Delta \varphi }\)
აქედან ψ = 0,23.
საბოლოოდ ჯამური რხევა ჩაიწერება ასე:
x = 13 cos(ωt + 0,23π).
პასუხი: x0= 13 სმ; \(tg\psi =\frac{x_{02\sin \Delta \varphi }}{x_{01}+x_{02}\cos \Delta \varphi }\).
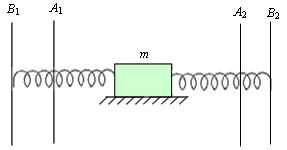
ma = -(k1+k2)x,
ანუ
.\(a+\frac{k_{1}+k_{2}}{m}x=0\)
ამ განტოლებაში \(\omega _{0}=\sqrt{\frac{k_{1}+k_{2}}{m}}\) - არის ტვირთის რხევის საკუთარი სიხშირე. როგორც ჩანს, ის არ არის დამოკიდებული ტვირთის წანაცვლებაზე. რხევის პერიოდი დაკავშირებულია საკუთარ სიხშირესთან ასე \(T=\frac{2\pi }{\omega _{0}}\) . შესაბამისად, არც პერიოდი არ არის დამოკიდებული ტვირთის წანაცვლებაზე.
პასუხი: რხევის პერიოდი არ იცვლება.
