ატომებს შორის უმარტივესი, წყალბადის ატომი ბორის თეორიისათვის თავისებურ ტესტ-ობიექტს წარმოადგენს. თეორიის შექმნის მომენტისთვის ის ექსპერიმენტულად კარგად იყო შესწავლილი. ცნობილი იყო, რომ ის შეიცავს ერთადერთ ელექტრონს. ატომის ბირთვი პროტონია, დადებითად დამუხტული ნაწილაკი, რომლის მუხტი სიდიდით ელექტრონის მუხტის ტოლია, ხოლო მასა 1836-ჯერ აღემათება ელექტრონის მასას.

ჯერ კიდევ XIX საუკუნის დასაწყისში აღმოაჩინეს დისკრეტული სპექტრული ხაზები წყალბადის ატომის გამოსხივების ხილულ სპექტრში (ე.წ. ხაზოვანი სპექტრი). შემდგომში კანონზომიერებები, რომლებიც ხაზოვანი სპექტრის ტალღის სიგრძეები (ან სიხშირეები) ემორჩილება, რაოდენობრივად კარგად იქნა შესწავლილი (ი.ბალმერი, 1885 წ.). წყალბადის ატომის გამოსხივების ხილულ სპექტრში სპექტრული ხაზების ერთობლიობას ბალმერის სერია უწოდეს. მოგვიანებით სპექტრული ხაზების ანალოგიური სერიები აღმოაჩინეს სპექტრის ულტრაიისფერ და ინფრაწითელ ნაწილში. 1890 წელს ი.რიდბერგმა მიიღო ემპირიული ფორმულა სპექტრული ხაზების სიხშირეებისთვის:

ბალმერის სერიისთვის m = 2, n = 3, 4, 5, ... . ულტრაიისფერი სერიისათვის (ლაიმანის სერია) m = 1, n = 2, 3, 4, ... . R მუდმივას რიდბერგის მუდმივა ეწოდება. მისი რიცხვითი მნიშვნელობაა R = 3,29·1015 ჰც. ბორამდე ხაზოვანი სპექტრის წარმოქმნის მექანიზმი და წყალბადის (ან სხვა ატომების) სპექტრული ხაზების ფორმულაში შემავალი მთელი რიცხვების არსი გაუგებარი რჩბოდა.
ბორის პოსტულატებმა განსაზღვრა ახალი მეცნიერების, ატომის ქვანტური ფიზიკის, განვითარება. მაგრამ ისინი არ შეიცავდნენ სტაციონალური მდგომარეობის (ორბიტების) პარამეტრების და მათი შესაბამისი ენერგიის En განსაზღვრის რეცეპტებს.
ბორის მიერ გამოცნობილი იქნა დაქვანტვის წესი, რომელიც ცდებთან თანხმობაში მყოფ წყალბადის ატომის სტაციონალური მდგომარეობების შესაბამის ენერგიებს განსაზღვრავს. მისი შემოთავაზებით, ბირთვის გარშემო მბრუნავი ელექტრონის იმპულსის მომენტს შეუძლია მხოლოდ დისკრეტული მნიშვნელობების მიღება, რომლებიც პლანკის მუდმივას ჯერადი იქნებიან. წრიული ორბიტებისთვის ბორისეული დაქვანტვის წესი შემდეგი სახით ჩაიწერება
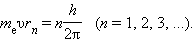
აქ me – ელექტრონის მასაა, υ – მისი სიჩქარე, rn – სტაციონალური წრიული ორბიტის რადიუსია. ბორის დაქვანტვის წესი წყალბადის ატომის ელექტრონის სტაციონალური ორბიტების რადიუსების და მათი შესაბამისი ენერგიების მნიშვნელობების განსაზღვრის საშუალებას იძლევა. ატომბირთვის კულონური ველის რაღაც r რადიუსის მქონე წრიულ ორბიტაზე მბრუნავი ელექტრონის სიჩქარე, ნიუტონის მეორე კანონიდან გამომდინარე, განისაზღვრება თანაფარდობით
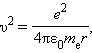
სადაც e – ელექტრონის მუხტია, ε0 – ელექტრული მუდმივა. ელექტრონის სიჩქარე υ და სტაციონალური ორბიტის რადიუსი rn ბორის დაქვანტვის წესით არიან დაკავშირებულნი. აქედან გამომდინარეობს, რომ სტაციონალური ორბიტის რადიუსები განისაზღვრება გამოსახულებით
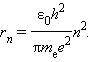
ბირთვთან ყველაზე ახლოს მყოფ ორბიტას შეესაბამება n = 1 მნიშვნელობა. პირველი ორბიტის რადიუსი, რომელსაც ბორის რადიუსად იწოდება, ტოლია

შემდეგი ორბიტების რადიუსები იზრდება n2-ს პროპორციულად.
ატომის ბირთვისა და rn რადიუსის მქონე სტაციონალურ ორბიტაზე მბრუნავი ელექტრონისაგან შედგენილი სისტემის სრული მექანიკური ენერგია ტოლია
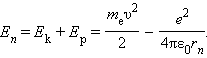
უნდა აღინიშნოს, რომ Ep < 0, რადგანაც ელექტრონსა და ბირთვს შორის მიზიდულობის ძალები მოქმედებს. ამ ფორმულაში υ2 და rn გამოსახულებების ჩასმით მივიღებთ:

მთელ რიცხვებს n = 1, 2, 3, ... ატომის ქვანტურ ფიზიკაში მთავარ ქვანტურ რიცხვებს უწოდებენ.
ბორის მეორე პოსტულატის თანახმად, ელექტრონის En ენერგიის მქონე ერთი სტაციონალური ორბიტიდან მეორე Em < En ენერგიის მქონე სტაციონალური ორბიტაზე გადასვლისას ატომი ასხივებს სინათლის ქვანტს, რომლის სიხშირე νnm ტოლია ΔEnm / h:

ეს ფორმულა ზუსტად ემთხვევა წყალბადის ატომის სპექტრული სერიების რიდბერგის ემპირიულ ფორმულას , თუ R მუდმივას ჩავთვლით

ტოლად.
ამ ფორმულაში me, e, ε0 და h-ს რიცხვითი მნიშვნელობების ჩასმით ვღებულობთ
R = 3,29·1015 ჰც.
რომელიც R -ს ემპირიულ მნიშვნელობასთან ძალიან კარგ თანხმობაშია. ნახ. 1 უჩვენებს წყალდაბის ატომის გამოსხივებისას სპექტრული სერიების წარმოქმნას ელექტრონის უფრო მაღალი სტაციონალური ორბიტიდან უფრო დაბალზე გადასვლისას.
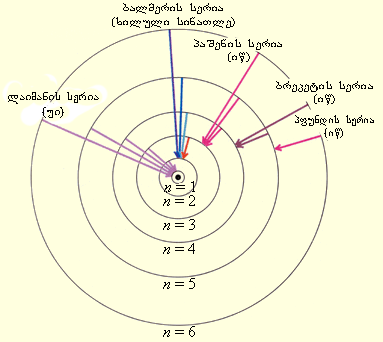
მან. 1.
წყალბადის ატომის სტაციონალური ორბიტები და სპექტრული ხაზების წარმოქმნა
ნახ. 2-ზე გამუსახულია წყალბადის ატომის სტაციონალური ორბიტების დიაგრამა და ნაჩვენებია სხვადასხვა სპექტრული სერიის შესაბამისი გადასვლები.
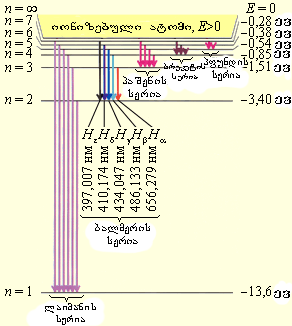
ნახ.2.
წყალბადის ატომის ენერგეტიკული დონეების დიაგრამა. ნაჩვენებია სხვადასხვა სპექტრული სერიის შესაბამისი გადასვლები. მითითებულია სპექტრის ხილული უბნის ბალმერის სერიის პირველი ხუთი ხაზის ტალღის სიგრძეები
წყალბადის ატომისთვის ბორის თეორიის საუკეთესო თანხმობა ექსპერიმენტთან ამ თეორიის სამართლიანობის სასარგებლო წონად არგუმენტს წარმოადგენდა. მაგრამ ამ თეორიის უფრო რთულ ატომებთან მიყენების მცდელობა წარუმატებლად დასრულდა. ბორმა ვერ შესძლო დაქვანტვის წესისთვის ფიზიკური ინტერპრეტაცია მიეცა. ეს ათწლეულით გვიან დე ბროილმა ნაწილაკის ტალღურ ბუნებაზე ცნებების საფუძველზე გააკეთა. დე ბროილის მიხედვით წყალდადის ატომის ყოველი ორბიტა შეესაბამება ტალღას, რომელიც ბირთვის მახლობელ წრეწირზე ვრცელდება. სტაციონალური ორბიტა წარმოიქმნება იმ შემთხვევაში, როცა ტალღა ბირთვის გარშემო ყოველი შემოვლისას უწყვეტად თავის თაცს იმეორებს. სხვა სიტყვებით, სტაციონალური ორბიტა შეესაბამება დე ბროილის წრიულ მდგარ ტალღას ორბიტის ტალღის სიგრძეზე (ნახ. 3). ეს მოვლენა ძალიან ჰგავს ბოლოებით დამაგრებულ სიმში აღძრული მდგარი ტალღის სტაციუნალურ სურათს.
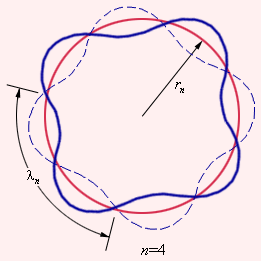
ნახ. 3.
n = 4 შესაბამისი სტაციონალური ორბიტაზე მდგარი ტალღის წარმოქმნის დე ბროილის იდეის ულუსტრაცია
დე ბროილის იდეის მიხედვით წყალბადის ატომის სტაციონალურ ქვანტურ მდგომარეობაში ორბიტის სიგრძეზე უნდა ეტეოდეს ტალღის სიგრძის λ-ს მთელი რიცხვი, ე.ი.
nλn = 2πrn.
ამ თანაფარდობაში დე ბროილის λ = h / p ტალღის სიგრძის ჩასმით, სადაც p = meυ – ელექტრონის იმპულსია, მივიღებთ:
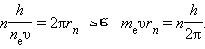
ამგვარად, ბორის დაქვანტვის წესი ელექტრონის ტალღურ თვისებებთანაა დაკავშირებული.
წყალბადის ატომის გამოსხივების სპექტრული კანონზომიერების ახსნაში ბორის თეორიის წარმატება განსაცვიფრებელი იყო. ნათელი გახდა, რომ ატომი ქვანტური სისტემაა, ხოლო ატომის სტაციონალური მდგომარეობების დონეები დისკრეტულია. ბორის თეორიის შექმნასთან ერთად, თითქმის ერთდროულად იქნა მიღებული ატომის სტაციონალური მდგომარეობებისა და ენერგიის დაქვანტვის პირდაპირი ექსპერიმენტული დასაბუთება. ატომის ენერგეტიკული დონეების დისკრეტილობა 1913 წელს იქნა ილუსტრირებული ჯ.ფრანკისად.ფრანკისა და ჰ.ჰერცის იმ ცდის საშუალებით, რომლითაც ვერცხლისწყლის ატომებთან ელექტრონების შეჯახების კვლევა ხდებოდა. აღმოჩნდა, რომ თუ ელექტრონის ენერგია 4,9 ევ-ზე ნაკლებია, მაშინ მათი ვერცხლისწყლის ატომებთან შეჯახება აბსოლუტურად დრეკადი დაჯახების კანონებით ხდება. თუ ენერგია 4,9ევ-ის ტოლია, მაშინ ვერცხლისწყლის ატომებთან შეჯახება არადრეკადი შეჯახების ხასიათს იძენს, ე.ი. ვერცხლისწყლის უძრავ ატომებთან შეჯახებისას ელექტრონები კინეტიკურ ენერგიას სრულად კარგავენ. ეს ნიშნავს, რომ ვერცხლესწყალი შთანთქავს ელექტრონის ენერგიას და ძირითადი მდგომარეობიდან პირველ აღგზნებულ მდგომარეობაში გადადის,
E2 – E1 = 4,9 ევ.
ბორის კონცეფციის თანახმად, უკან თვითნებული გადასვლისას ვერცხლისწყლის ატომი უნდა ასხივებდეს ქვანტს სიხშირით
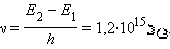
ასეთი სიხშირის სპექტრული ხაზი ვერცხლისწყლის ატომის გამოსხივების სპექტრის ულტრაიისფერ უბანში მართლაც იქნა აღმოჩენილი.
დისკრეტული მდგომარეობების ცნება კლასიკურ ფიზიკას ეწინააღმდეგება. ამიტომაც დაისვა კითხვა, ქვანტური თეორია კლასიკური ფიზიკის კანონებს ხომ არ უარყოფს.
ქვანტურ თეორიას ენერგიის, იმპულსის, ელექტრული მუხტის და სხვ. შენახვის ფუნდამენტური კლასიკური კანონები არ გაუუქმებია. ბორის მიერ ჩამოყალიბებული შესაბამისობის პრინციპის მიხედვით, ქვანტური ფიზიკა მოიცავს კლასიკური ფიზიკის კანონებს, გარკვეულ პირობებში შეინიშნება ქვანტური ცნებებიდან კლასიკურზე მდორე გადასვლა. ამის დანახვა შეიძლება წყალბადის ატომის ენერგეტიკული სპექტრის მაგალითზე (ნახ. 2). დიდი ქვანტრური რიცხვებისას n >>1 დისკრეტული დონეები თანდათანობის უახლოვდებიან ერთმანეთს, და ხდება მდორე გადასვლა უწყვეტი სპექტრის უბანში, რომელიც კლასიკური ფიზიკიდან გამოდის.
ორნაწილიანი, ბორის ნახევრადკლასიკური თეორია ქვანტური წარმოდგენების განვითარების მნიშვნელოვან ეტაპს წარმოადგენდა, რომელთა ფიზიკაში შემოტანამაც მექნიკასა და ელეტროდინამიკაში კარდინალური გარდაქმნები მოითხოვა. ასეთი გადაქმნები XX საუკუნის 20-ან - 30-იან წლებში განხორციელდა.
ბორის წარმოდგენები გარკვეულ ორბიტებზე. რომლებზედაც ელექტრონები მოძრაობდნენ, საკმაორ პირობითი აღმოჩნდა. სინამდვილეში ატომებში ელექტრონების მოძრაობა ძალიან ცოტათი ჰგავს პლანეტების და თანამგზავრების მოძრაობას. ფიზიკური აზრი აქვს ელექტრონის ამა თუ იმ ადგილზე აღმოჩენის ალბათობას, რომელიც ტალღური ფუნქციის კვატრატით |Ψ|2 აღიწერება. ტალღური ფუნქცია Ψ ქვანტური მექანიკის ძირითადი განტოლების, შრედინგერის განტოლების ამოხსნას წარმოადგენს. აღმოჩნდა, რომ ატომში ელექტრონის მდგომარეობა მთელი რიგი ქვანტური რიცხვებით ხასიათდება. მთავარი ქვანტური რიცხვი n ატომის ქვანტურ ენერგიას განსაზღვრავს. იმპულსის მომენტის დაქვანტვისათვის შემოტანილია ე.წ. ორბიტული ქვანტური რიცხვი l. იმპულსის მომენტის გეგმილი სივრცის ნებისმიერ გამოყოფილ მიმართულებაზე (მაგალითად, მაგნიტური ველის \(\vec{B}\) ვექტორის მიმართულება) ასევე მნიშვნელობების დისკრეტულ რიგს იღებს. იმპულსის მომენტის გეგმილის დაქვანტვისათვის შემოტანილია მაგნიტური ქვანტური რიცხვი m. n, l, m ქვანტური რიცხვები დაქვანტვის გარკვეული წესებით არიან დაკავშირებული. მაგალითად, ორბიტული ქვანტური რიცხვი l შეიძლება ღებულობდეს მთელი რიცხვების მნიშვნელობას 0-დან (n – 1)-მდე. მაგნიტური ქვანტური რიცხვი m შეიძლება ღებულობდეს მთელი რიცხვების მნიშვნელობას ±l-ს ინტერვალში. ამგვარად, მთავარი ქვანტური n რიცხვის ყოველ მნიშვნელობას, რომელიც ატომის ენერგეტიკულ მდგომარეობას განსაზღვრავს, l და m ქვანტური რიცხვების კომბინაციების მთელი რიგი შეესაბამება. ყოველ ასეთ კომბინაციას ელექტრონის სივრცის სხვადასხვა წერტილში აღმოჩენის |Ψ|2 ალბათობის გარკვეული განაწილება შეესაბამება („ელექტრული ღრუბელი“).
მდგომარეობა, როცა ორბიტული ქვანტური რიცხვი l = 0-ს, აღიწერება ალბათობების სფერულ სიმეტრიული განაწილებებით. მათ s-მდგომარეობები ეწოდებათ (1s, 2s, ..., ns, ...). როცა l > 0 ელექტრული ღრუბლის სფერული სიმეტრია ირღვევა. l = 1-ს შესაბამის მდგომარეობას p-მდგომარეობას უწოდებენ, l = 2-სას - d-მდგომარეობას და ა.შ.
ნახ. 4-ზე წყალბადის ატომში ელექტრონის ბირთვიდან სხვადასხვა 1s და 2s მანძილებზე აღმოჩენის ρ (r) = 4πr2|Ψ|2 ალბათობის განაწილების მრუდებია გამოსახული.

ნახ. 4.
წყალბადის ატომში ელექტრონის 1s და 2s მდგომარეობებში აღმოჩენის ალბათობის განაწილება. r1 = 5,29·10–11მ - ბორის პირველი ორბიტის რადიუსია
როგორც ნახ. 4-დან ჩანს, 1s მდგომარეობაში (წყალბადის ატომის ძირითადი მდგომარეობა) ელექტრონი შეიძლება ბირთვიდან სხვადასხვა მანძილზე აღმოჩნდეს. უდიდესი ალბათობით შეიძლება აღმოჩნდეს მანძილზე, რომელიც ბორის პირველი ძიროთადი ორბიტის რადიუსს r1-ს ტოლია. 2s მდგომარეობაში ელექტრონის აღმოჩენის ალბათობა მაქსიმალურია ბირთვიდან r = 4r1 მანძილზე. ორივე შემთხვევაში წყალბადის ატომი შიძლება წარმოვიდგინოთ სფერულად სიმეტრიული ელექტრონული ღრუბლის სახით, რომლის ცენტრშიც ბირთვია მოთავსებული.


