ნიუტონის კლასიკური მექანიკა მშვენივრად აღწერს მცირე (υ << c) სიჩქარეების მქონე მაკროსხეულების მოძრაობას. არარელატივისტურ ფიზიკაში ერთიანი მსოფლიო დროის არსებობა აშკარა ფაქტად იყო მიღებული. კლასიკური მექანიკას სფუძვლად უდევს ფარდობითობის მექანიკური პრინციპი (ან გალილეის ფარდობითობის პრინციპი): მექანიკის კანონები ერთნაერია ათვლის ყველა ინერციულ სისტემაში. ეს პრინციპი ნიშნავს, დინამიკის კანონები ინვარიანტულია (ე.ი. უცვლელია) გალილეის გარდაქმნების მიმართ, რომელიც საშუალებას იძლევა გამოითვალოს მოძრავი სხეულის კოორდინატები ერთ ინეციულ სისტემაში (K), თუ მოცემულია ამ სხეულის კოორდინატები მეორე ინერციულ სისტემაში (K'). კერძო შმთხვევაში, როცა K' სისტემა K სისტემის ღერძის გასწვრივ მისი დადებითი მიმართილებით υ სიჩქარით მოძრაობს (ნახ. 1), გალილეის გარდაქმნებს აქვთ სახე:
x = x' + υt, y = y', z = z', t = t'.
იგულისხმება, რომ საწყის მომენტში ორივე სისტემის სათავე ერთმანეთს ემთხვევა.
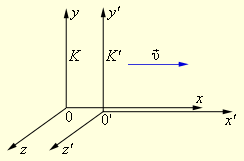
ნახ. 1.
ათვლის ორი K და K' ინერციული სისტემა
გალილეის გარდაქმნებიდან გამოდის ერთი ინერციული სისტემიდან მეორეზე გადასვლისას სიჩქარეების გარდაქმნის კლასიკური კანონი:
ux = u'x + υ, uy = u'y, uz = u'z.
სხეულის აჩქარება ყველა ინერციულ სისტემაში ყოველთვის ერთნაერია:
აქდან გამომდიმარე კალასიკურ მექანიკაში მოძრაობის განტოლება (ნიუტონის მეორე კანონი)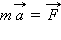 
არ იცვლის სახეს ერთი ინერციული სისტემიდან მეორეში გადასვლისას.
XIX საუკუნის ბოლოს დაგროვება დაიწყო ცდისეულმა ფაქტებმა, რომლებიც კლასიკური მექანიკის კანონებს ეწინააღმსეგებოდნენ. დიდი სირთულეები წარმოიშვა სინათლის გავრცელების ნიუტონის მექანიკით ახსნის მცდელობისას. იმის დაშვება, რომ სინათლე განსაკუთრებულ გარემოში - ეთერში - ვრცელდება, მრავალმა ექსპერიმენტმა უარყო. ამერიკელმა ფიზიკოსმა ა.მაიკელსონმაა.მაიკელსონმა 1881 წელს ჯერ დამოუკიდებლად, შემდეგ კი ე.მორლისთან ერთად 1887 წელს ინტერფერენციული მეთოდით ცდილობდა აღმოეჩინა დედამიწის მოძრაობა ეთერის მიმართ („ეთერის ქარი“). მაიკელსონ-მოპლის ცდის გამარტივებული სქემა ნახ. 2-ზეა მოცემული.
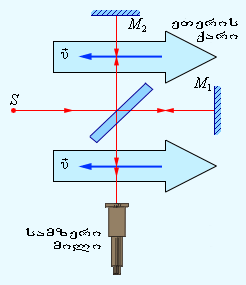
ნახ. 2.
მაიკელცინ-მოპლის ინტერფერენციული ცდის გამარტივებული სქემა. \(\vec{v}\) – დედამიწის ორბიტული სიჩქარე
ამ ცდაში მაიკელსონის ინტერფერომეტრის ერთ-ერთი მხარი დედამიწის ორბიტული სიჩქარის (υ = 30 კმ/წმ) პარალელურადაა მიმართული. შემდეგ ხელსაწყო ბრუდეაბა 90°-ით, და ორბიტული სიჩქარის გასწვრივ ორიენტირებული ახლა მეორე მხარი აღოჩნდება. გამოთვლებმა აჩვენეს, რომ უძრავი ეთერი რომ არსებობდეს, შემობრუნებისას ინტერფერენციული ზოლები (υ / c)2-ს პროპორციულ მანძილზე უნადა გადანაცვლებულიყვნენ. მაიკელცინ-მოპლის ცდამ, რომელიც არაეთხელ განმეორდა სულ უფრო მზარდი სიზუსტით, უარყოფითი შედეგი აჩვენა. მაიკელსონ-მოპლის ცდის შედეგების ანალიზმა და რამოდენიმე სხვა ექსპერიმენტმა შესაძლებელი გახადა დაესკვნათ, რომ წარმოდგენა ეთერზე, როგორც გარემოზე, რომელშიც სინათლის ტალღები ვრცელდებიან მცდარი იყო. აქედან გამომდინარე, სინათლისათვის არ არსებობს გამორჩეული (აბსოლუტური) ათვლის სისტემა. დედამიწის ორბიტაზე მოძრაობა არ მოქმედებს დედამიწაზე მიმდინარე ოპტიკურ მოვლენებზე.
სივრცისა და დროის შესახებ წარმოდგენის განვითარებაში გამორჩეული როლი მაქსველის თეორიამ შეასრულა. XX საუკუნის დასაწყისში თეორია საყოველთაოდ მიღებული გახდა. მაგრამ მაქსველის თეორიიდან გამოდის, რომ ელექტრომაგნიტური ტალღების გავრცელების სიჩქარეს ნებისმიერ ინერციულ სისტემაში ერთიდაიგივე მნიშვნელიბა აქვს, რომელიც ვაკუუმში სინათლის სიჩქარის ტოლია. ეს ნიშნავს, რომ განტოლება, რომელიც ელექტრომაგნიტური ტალღების გავრცელებას აღწერს, ინვარიანტული არ არის გალილეის გარდაქმნების მიმართ. თუ ელექტრომაგნიტური ტალღა (კერძოდ, სინათლე) K' სისტემაში ვრცელდება (ნახ. 1) x' ღერძის დადებითი მიმართულებით, მაშინ K სისტემაში გალილეის კინეტიკის თანახმად გავრცელდება c + υ-ით, და არა c -თი.
ამგავარად, XIX და XX საუკუნეების მიჯნაზე ფიზიკა კრიზისს განიცდიდა. გამოსავალი აინშტაინმა სივრცესა და დროზე კლასიკურ წარმოდგენებზე უარის თქმით იპოვა. ამ გზაზე უმნიშვნელოვანესი ნაბიჯი კლასიკურ ფიზიკაში გამოყენებული აბსოლუტური დროის ცნების გადასინჯვა იყო. კლასიკური წარმოდგენები, რომლებიც აშკარა და ნათელის შთაბეჭდილებას ტოვებს, სინამდვილეში არ გამართლდა. მრავალი ცნება და სიდიდე, რომლებიც არარელატივისტურ ფიზიკაში ითვლებოდა აბსოლუტურად, ე.ი. ათვლის სისტემისგან დამოუკიდებლად, ეინშტეინის ფარდობითობის თეორიაში გადაყვანილია ფარდობითობის რიგში.
რადგანაც, ყველა ფიზიკური მოვლება სივრცესა და დროში ხდება, სივრცულ-დროითი კანონზომიერების ახალ სისტემას არ შეეძლო არ შეხებოდა მთელ ფიზიკას.
ფარდობითობის სპეციალური თეორიის საფუძველში ორი პრინციპი ანუ პოსტულადი დევს, რომელიც ეაინშტაინმა ჩამოაყალიბა 1905 წელს.
- ფარდობითობის პრინციპი: ბუნების ყველა კანონი ინვარიანტულია ერთი ინერციული სისტემიდან მეორეში გადასვლის მიმართ. ეს ნიშნავს, რომ ინერციულ სისტემებში ფიზიკურ კანონებს (არა მარტო მექანიკის) ერთნაერი ფორმა აქვთ. ამგვარად, კლასიკური მექანიკის ფარდობითობის პრინციპი განზოგადდება ბუნების ყველა მოვლენაზე, მათ შორის ელექტრომაგნიტურებზეც. ამ განზოგადებულ პრინციპს აინშტაინის ფარდობითობის პრინციპი ეწოდება.
- სინათლის სიჩქარის ფარდობითობის პრინციპი: ვაკუუმში სინათლის სიჩქარე არ არის დამოკიდევული წყაროს ან დამკვირვებლის მოძრაობის სიჩქარეზე და ყველა ათვლის ინერციულ სისტემაში ერთნაერია. ფარდობითობის სპეციალურ თეორიაში სინათლის სიჩქარეს განსაკუთრებული ადგილი უჭირავს. ეს ურთიერთქმედების და სიგნალის სივრცის ერთი წერტილიდან მეორეში გადაცემის ზღვრული სიჩქარეა.
ეს პრინციპები უნდა განიხილებოდეს როგორც ცდისეული ფაქტების ერთობლიობის განზოგადება. ამ პრინციპებზე დაყრდნობით შექმნილი თეორიის შედეგები უამრავი ცდისეული შემოწმებებით დასტურდებოდა. ფარდობითობის სპეციალურმა თეორიამ გადაჭრა „აინშტაინამდე“ ფიზიკის ყველა პრობლემა და ახსნა ელექტროდინამიკისა და ოპტიკის იმ დროისათვის ცნობილი ექსპერიმენტების „ურთიერთგამომრიცხავი შედეგები. შემდგომში ფარდობითობის სპეციალური თეორია გამაგრებული იყო ექსპერიმენტული ფაქტებით, როლებიც მიღებული იყო ამაჩქარებელში სწრაფი ნაწილაკების მოძრაობის, ატომური პროცესების, ბირთვული რეაქციების და ა.შ. შესწავლისას.
ფარდობითობის სპეციალური თეორიის პოსტულატები კლასიკურ წარმოდგენებთან მკაფიო წინააღმდეგობაშია. განვიხილოთ ასეთი აზრობრივი ექსპერიმენტი: t = 0 დროის მომენტში, როცა ორი K და K' ინერციული სისტემის საკოორდინატო ღერძები ერთმანეთს ემთხვევა, კოორდინატთა საერთო სათავეში მოხდა სინათლის ხანმოკლე ანთება. t დროის განმავლობაში სისტემებმა ერთმანეთის მიმართ υt მანძილით გადაადგილდნენ, ხოლო სფერულ ტალღის ფრონტს თითოეულ სისტემაში ექნება ct რადიუსი (ნახ. 3), რადგანაც სისტემები ტოლუფლებიანნი არიან და სინათლის სიჩქარე ორივეში ტოლია c -სი.
ნახ. 3.
ფარდობითობის სპეციალური თეორიის პოსტულატების მოჩვენებითი წინააღმდეგობა.
K სისტემის დამკვირვებლისათვის სფეროს ცენტრი O წერტილში მდებარეობს, ხოლო K' სისტემის დამკვირვებლისათვის ის O' წერტილში იქნება. აქდან გამომდინარე,სფერული ფრონტის ცენტრი ერთდროულად ორ სხვადასხვა წერტილში იმყოფება!
წარმოქმნილი გაუგებრობის მიზეზი ფარდობითობის სპეციალური თეორიის პოსტულატებს შორის წინააღმდეგობაში კი არ არის, არამედ იმ დაშვებაში, რომ სფერული ტალღის ფრონტი ორივე სისტემისათვის დროის ერთსადაიმავე მომენტს განეკუთვნება. ეს დაშვება გალილეის გარდაქმნის ფორმულებშია ჩადებული, რომლის მიხედვითაც დრო ორივე სისტემაში ერთნაერად მიმდინარეობს: t = t'. აქედან გამომდინარე, აინშტაინის პოსტულატები ერთმანეთს კი არ ეწინააღმდეგებიან, არამედ გალილეის გარდაქმნებს. ამიტომაც გალილეის გარდაქმნების მაგივრად ფარდობითობის სპეციალურმა თეორიამ ერთი ინერციული სისტემიდან მეორეზე გადასასვლელად სხვა გარდაქმნის ფორმილები - ე.წ. ლორენცის გარდაქმნები გამოიყენა, რომლებიც სინათლის სიჩქარის მახლობელი სიჩქარეებისათვის, საშუალებას იძლევა აიხსნას ყველა რელატივისტური ეფექტი, ხოლო დაბალი (υ << c) სიჩქარეებისათვის კი გალილეის გარდაქმნების ფორმულებში გადადიან. ამგვარად, ახალმა თეორიამ (ფარდობითობის სპეციალურმა თეორიამ) ძველი კლასიკური თეორია კი არ უარყო, არამედ დააზუსტა მისი გამოყენების საზღვრები. ძველ და ახალ, უფრო ზოგად თეორიას, რომელიც ძველს ისე შეიცავს როგორც სასაზღვრო შემვევას, შორის კავშირს შესაბამისობის პრინციპი ეწოდება.