ინტერფერენცია სინათლის ტალღური ბუნების ერთ-ერთ აშკარა გამოვლინებაა. ეს საინტერესი და ლამაზი მოვლენა ორი ან რამდენიმე სინათლის კონის ურთიერთზედდების დროს დაიკვირვება. კონების გადაფარვის უბაში სინათლის ინტენსივობა ნათელი და ბნელი ზოლების მიმდევრობით ხასიათდება. ამასთან მაქსიმუმებში ინტენსივობა კონების ჯამურ ინტენსივობაზე მეტია, ხოლო მონიმუმებში ნაკლები. თეთრი სინათლის გამოყენებისას ინტერფერენციული ზოლები სპექტრის სხვადასხვა ფერებადაა შეფერილი. ინტერფერენციულ მოვლენებს საკმაოდ ხშირად ვხვდებით: ასფალტზე ზეთოვანი ლაქების ფერები, ფანჯრის გაყინული მინების შეფერილობა, ლამაზი შეფერილობის ნახატები ზოგიერთი პეპლისა და ხოჭოს ფრთებზე. ყველაფერი ეს ინტერფერევციის გამოვლინებაა.
სინათლის ინტერფერენციის ლაბორატორიულ პირობებში დაკვივების პირველი ექსპერიმენტი ნიუტონს ეკუთვნის. ის აკვირდებოდა ინტერფერენციულ სურათს, რომელიც მინის ბრტყელ ფირფიტასა და დიდი სიმრუდის რადიუსის მქონე ბრტყელ-ამოზნექილ ლინზას შორის თხელ ჰაერის ფენაში სინათლის არეკვლისას წარმოიქმნებოდა (ნახ. 1). ინტერფერენციულ სურათს კონცენტრული რგოლების სახე ჰქონდათ და მათ ნიუტონის რგოლებს უწოდებენ (ნახ. 2).
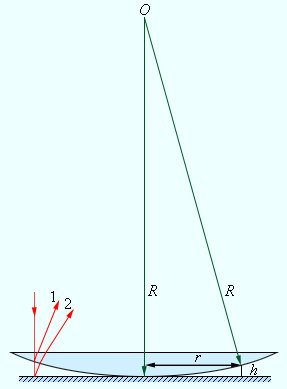
ნახ. 1.
ნიუტონის რგოლების დაკვირვება. ინტერფერენცია წარმოიქმნება ჰაერის ფენის ორი მხრიდან არეკვლილი ტალღების შეკრების შედეგად. სხივი 1 და 2 - ტალღის გავრცელების მიმართულება; h - ჰაერის ფენის სისქე
ნახ. 2.
ნიუტონის რგოლები სინათლის მწვანე და წითელ ფერებში
ნიუტონმა კორპუსკულარული თეორიის თვალსაზრისით ვერ შეძლო აეხსნა, თუ რატომმ წარმოიქმნებიან რგოლები, მაგრამ მას ესმოდა, რომ ეს დაკავშირებული იყო სინათლის რაღაც პერიოდულ პროცესებთან.
პირველი ინტერფერენციული ცდა, რომელიც სინათლის ტალღური ბუნებით აიხსნა იუნგის ცდა იყო (1802 წ.). იუნგის ცდაში სინათლე წყაროდან, რომლის მაგივრიბასაც ვიწრი S ხვრელი ასრულებდა, ეცემოდა ეკრანზე ერთმანეთთან ახლოს განლაგებულ S1 და S2 ხვრელებს (ნახ. 3). თითოეულ ხვრელში გასვლის შემდეგ სინათლის ნაკადი დიფრაქციის გამო ფართოვდებოდა, ამიტომ თეთრ ეკრანზე S1 და S2 ხვრელებიდან გამოსული სინათლის ნაკადები ერთმანეთს ფარავდნენ. გადაფარვის არეში დაიკვირვებოდა ინტერფერენციული სურათი ნათელი და ბნელი ზოლების მონაცვლეობის სახით.
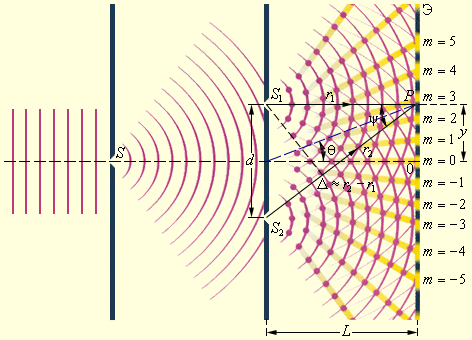
ნახ. 3.
იუნგის ინტერფერენციული ცდის სქემა
იუნგი პირველი მიხვდა, რომ ინტერფერენციის დაკვირვება არ შეიძლება ორი სხვადასხვა დამოუკიდებელი წყაროს ტალღების ზედდების დროს. ამიტომ მის ცდაში S1 და S2 ხვრელები, რომლებიც ჰიუგენსის პრინციპის შესაბამისად შეიძლება განხილულ იყოს, როგორც ერთი S წყაროთი განათებული მეორადი ტალღის წყაროები. მეორადი ტალღის წყაროების სიმეტრიულად განლაგებისას, S1 და S2 ხვრელებიდან გამოსული ტალღები ფაზაში იმყოფებიან, მაგრამ ისნი დაკვირვების P წერტილამდე სხვდასხვა r1 და r2 მანძილებს გადიან. ამიტომ, რხევის ფაზა, რომელსაც S1 და S2 წყაროები P წერტილში ქმნიან, განსხვავებულია. ამგვარად, ამოცანა ტალღების ინტერფერენციის შესახებ ერთიდაიგივე სიხშირის, მაგრამ სხვადასხვა ფაზის მქონე ტალღების შეკრების ამოცანაზე დაიყვანება. მტკიცება იმის შესახებ, რომ S1 და S2 წყაროებიდან ტალღები ვრცელდებიან ერთმანეთისგან დამოუკიდებლად, ხოლო დაკვირვების წერტილში კი უბრალოდ იკრიბებიან, ცდით მიღებული ფაქტია და სუპერპოზიციის სახელს ატარებს.
მონოქრომატული (ან სინუსოიდური) ტალღა, რომელიც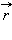 
რადიუს-ვექტორის მიმართულებით ვრცელდება, ჩაიწერება შემდეგი სახით
E = a cos (ωt – kr),
სადაც a – ტალღის ამპლიტუდაა, k = 2π / λ – ტალღური რიცხვია, λ – ტალღის სიგრძეა, ω = 2πν – წრიული სიხშირე. ოპტუკურ ამოცანებში ტალღის ელექტრული ველეს E დაძაბულობის ვექტორის სიდიდეა. P წერტილში ორი ტალღის შეკრების შედეგად მიღებული რხევა იგივე ω სიშირეზე ხდება და აქვს რაღაც A ამპლიტუდა და φ ფაზა:
E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ).
ხელსაწყოები, რომლებიც სინათილს ტალღის სწრაფ ცვლივებას ადევნებდნენ თვალს, არ არსებობს; დასაკვირვებელ სიდიდე ნაკადის ენერგიაა, რომელიც ტალღის ელექტრული ველის ამპლიტუდის კვადრატის პირდაპირპრიპირციულია. ტალღის ელექტრული ველის ამპლიტუდის კვადრატის ტოლ ფიზიკურ სიდიდეს ინტენსივობას უწოდებენ: I = A2.
იოლი ტრიგონიმეტრიული გარდაქმნები, P წერტილში მიღებული რხევისთვის შემდეგ გამოსახულებას იძლევა:
(*)
სადაც Δ = r2 – r1 – ე.წ. სვლათა სხვაობაა.
ამ გამოსახულებიდან გამოდის, რომ ინტერფერენციული მაქსიმუმი (ნათელი ზოლი) მიიღწევა სივრცის იმ წერტილებში, სადაც Δ = mλ (m = 0, ±1, ±2, ...). ამასთან Imax = (a1 + a2)2 > I1 + I2. ინტერფერენციული მინიმუმი (ბნელი ზოლი) როცა Δ = mλ + λ / 2. ინტენსივობის მინიმალური მნიშვნრლობა Imin = (a1 – a2)2 < I1 + I2. ნახ. 4-ზე ინტერფერენციულ სურათზე ინტენსივობის განაწილების Δ სვლათა სხვაობაზე დამოკიდებულებაა გამოსახული.
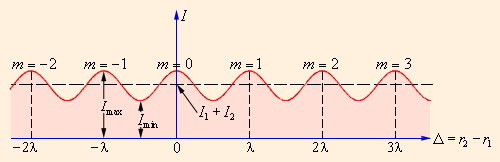
ნახ. 4.
ინტერფერენციულ სურათზე ინტენსივობის განაწილება. m მთელი რიცხი – ინტერფერენციული მაქსიმუმის რიგია
კერძოდ, თუ I1 = I2 = I0, ე.ი. ორივე ტალღის ინტენსივიბა ერთნაერია, (*) გამოსახულება ღებულობს სახეს:
I = 2I0(1 + cos kΔ). (**)
ამ შემთხვევაში Imax = 4I0, Imin = 0.
(*) და (**) ფორმულები უნივერსალური ფორმულები არიან. ისინი ინტერფერენციული სქემისათვისაა სამართლიანი, რომელშიც ორი ერთიდაიგივე სიხშირის მონოქრომატული ტალღის შეკრება ხდება.
თუ იუნგის სქემაში y -ით დაკვირვების წერტილის სიმეტრიის სიბრტყიდან წანაცვლებას ავღნიშნავთ, მაშინ შემთხვევისათვის, როცა d << L и y << L (ოპტიკურ ექსპერიმენტებში ეს პირობები ჩვეულებრივ სრულდება), მიახლოებით შეიძლება მივიღოთ:
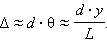
კოორდინატთა y ღერძის გასწვრის, ინტერფერენციული ზოლის სიგანის ტოლ Δl მანძილზე გადაადგილებისას, ე.ი. ერთი ინტერფერენციული მაქსიმუმიდან მეზობელ მაქსიმუმზე გადასვლისას, სვლათა სხვაობა Δ ტალღის ერთი λ სიგრძით იცვლება. აქედან გამომდინარე
სადაც ψ – დაკვირვების P წერტილში „სხივების“ თავმოყრის კუთხეა. შევასრულოთ რაოდენობრივი შეფასებები. დავუშვათ, რომ S1 და S2 ხვრელებს შორის d მანძილი 1 მმ-ს ტოლია, ხოლო ხვრელებიდან Э ეკრანამდე კი L = 1 მ, მაშინ ψ = d / L = 0,001 რად. მწვანე სინათლისათვის (λ = 500 ნმ) მივიღებთ Δl = λ / ψ = 5 · 105 ნმ = 0,5 მმ. წითლისათვის (λ = 600 ნმ) Δl = 0,6 მმ. ასეთი გზით იუნგმა პირველად გაზომა სინათლის ტალღების სიგრძეები, თუმცა ამ გაზომვების სიზუსტე დიდ არ იყო.
ხაზი უნდა გაესვას იმ გარემოებას, რომ ტალღურ ოპტიკაში, გეომეტრული ოპტიკისგან განსხვავებით, სინათლის სხივის ცნება ფიზიკურ აზრს კარგავს. ტერმინი „სხივი“ აქ ტალღის მიმართულების აღნიშვნის გასამარტივებლად გამოიყენება. შემდეგში ამ ტერმინს ბრჭყალების გარეშე გამოვიყენებთ.
ნიუტონის ექსპერიმენტში (ნახ. 1) ტალღოს ლინზის ზედაპირზე ნორნალური (მართობული) დაცემისას სვლათა სხვაობა დაახლოებით ლინზასა და ბრტყელ ფირფიტას შორის ჰაერის გაორმაგებული 2h სისქის ტოლია. იმ შემთხვევისთვის როცა ლინზის სიმრუდის რადიუსი R დიდია h-თან შედარებით, შეიძლება მიახლოებით მივიღოთ:
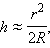
სადაც r – სიმეტრიის ღერძიდან გადახრაა. სვლათა სხვაობის გამოსახულებისათვის, აგრეთვე უნდა გავითვალისწონოთ, რომ 1 და 2 ტალღები სხვადასხვა პირობებში აირეკლებიან. პირველი ტალღა აირეკლება მინა-ჰაერის საზღვრიდან, ხოლო მეორე ჰაერი-მინის საზღვრიდან. მეორე შემთხვევაში ხდება რხევის ფაზის ცვლილება π -თი, რაც ექვივალენტურად ზრდის სვლას λ / 2-ით. ამიტომ:
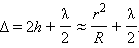
როცა r = 0, ანუ ცენტრში (შეხების წერტილი) Δ = λ / 2; ამიტომ ნიუტონი რგოლის ცენტრში ყოველთვის ინტერფერენციული მინიმუმი დაიკვირვება, ე.ი. ბნელი ზოლი. შემდეგი ბნელი ზოლების rm რადიუსი განისაზღვრება გამოსახულებით
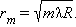
ეს ფორმულა საშუალებას იძლევა ექსპერიმენტულად განისაზღვროს λ ტალღის სიგრძე, თუ ცნიბულია ლინზის სიმრუდის რადიუსი R.
კოჰერენტული ტალღების პრობლემა. იუნგის თეორიის საფუძველზე აიხსნა ორი ერთნაერი სიხშირის მქონე მონოქრომატული ტალღის შეკრებით მიღებული ინტერფერენციული მოვლენა. მაგრამ ყოველდღიური გამოცდილება გვიჩვენებს, რომ სინათლის ინტერფერენციის დაკვირვების სინამდვილეში არც ისე ადვილია. თუ ოთახში ორი ერთნაერი ნათურა ანთია, ოთახის ყოველ წერთილში სინათლის ინტენსივიბები იკრიბება და არავითარი ინტერფერენცია არ დაიკვირვება. ისმის კითხვა, როგორ შემთხვევებში უნდა იკრიბებოდეს დაძაბულობები (ფაზათა თანაფარდობის გათვალისწინებით), როგორი ტალღის ინტენსივობები, ე.ი. დაძაბულობის კვადრატები? მონოქრონატული ტალღების ინტერფერენციის თეორია ამ კითხვაზე პასუხს ვერ იძლევა.
სინათლის რეალური ტალღები მკაცრად მონოქრომატული არ არის. ფუნდამენტური ფიზიკური მიზეზების გამო გამოსხივებას ყოველთვის აქვს სტატისტიკური (ან შემთხვევითი) ხასიათი. სინათლის წყაროს ატომები ერთმანეთისაგან დამოუკიდებლად ასხივებენ დროის შემთხვევით მომენტებში და თითოეული ატომის გამოსხივება ძალის მცირე ხანგრძლიობისაა (τ ≤ 10–8 წმ). წყაროს სრული გამოსხივება ყოველ მომენტში შედგება აურაცხელი ატომების წვლილისგან. τ რიგის დროის შემდეგ ატომების გამოსხივებათა მთელი ერთობლიობა განახლდება. ამიტომაც ჯამურ გამოსხივებას ექნება სხვა ამპლიტუდა და სხვა ფაზა. რეალური დენის წყარის მიერ გამოსხივებული ტალღის ფაზა მიახლოებით უცვლელი რჩება მხოლოდ τ რიგის დროის ინტერვალებში. τ ხანგრძლივობის გამოსხივების ცალკეული „ნაწყვეტებს“ ცუგებს უწოდებენ. ცუგებს cτ-ის ტოლი დროითი სიგრძე აქვტ, სადაც c – სინათლის სიჩქარეა. სხვადასხვა ცუგის რხევა ერთმანეთთან შეთანხმებილი არ არის. ამგვარად, სინათლის რეალური ტალღა, უწესრიგოდ ცვლადი ფაზების მქონე, ტალღური ცუგების მიმდევრობას წარმოადგენს. ამბობენ ხოლმე, რომ სხვადასხვა ცუგების რხევები არაკოჰერენტულია. τ დროის ინტერვალი, რომლის განმავლობაშიაც რხევის ფაზა მიახლოებით უცვლელი რჩება, კოჰერენტულობის დროს უწოდებენ.
ინტერფერენცია შეიძლება წარმოიშვას მხოლოდ კოჰერენტული რხევის შემთხვევაში, ე.ი. რხევისა რომელიც ერთიდაიგივე ცუგას ეკუთვნის. მიუხედავად იმისა, რომ ყოველი ცუგის ფაზა ასევე ექვემდებარება დროში შემთხვევით ცვლილებას, ეს ცვლილებები ერთნაერია, ამიტომაც კოჰერენტული რხევების ფაზათა სხვაობა უცვლელი რჩება. ასეთ შემთხვევაში მდგრადი ინტერფერენციული სურათი დაიკვირვაბა და ე.ი. სრულდება ველების სუპერპოზიციიც პრინციპი. კოჰერენტული რხევების შეკრებისას ფაზათა სხვაობა დროის შემთხვევითი ფუნქციაა. ინტერფერენციული ზოლები განიცდიან აქეთ-იქეთ უწესრუგი გადააგგილებას, და მათი რეგისტრაციის Δt დროის განმავლობაში, რომელიც ოპტიკურ ექსპერიმენტებში კოჰერენტულობის დროზე გაცილებით მეტია (Δt >> τ), სრული გასაშუალოება ხდება. მარეგისტრურებელი მოწყობილობა (თვალი, ფოტოფირფიტა, ფოტოელემენტი ან ნებისმიერი სხვა მიმღები) დაკვირვების მომენტში დააფიქსირებს ინტენსივობის გასაშუალებულ მნიშვნელობას, რომელიც ორივე რხევის ინტენსივობების ჯამის I1 + I2 ტოლია. ამ შემთხვევაში სრულდება ინტენსივობების შეკრების კანონი.
ამგვარად, ინტერფერენცია მხოლოს კოჰერენტილი რხევების შეკრებისას შეიძლება წარმოიქნმას. დაკვირვების წერტილში კოჰერენტული რხევებით მიღებულ ტალღებსაც კოჰერენტულს უწოდებენ. ორი დამოუკიდებელი წყაროს ტალღები არაკოჰერენტულია და ინტერცერენციას ვერ შექმნიან. იუგმა ინტუიციურად მიაგნო, რომ სინათლის ინტერფერენციის მისაღებად საჭიროა წყაროდან მომავალი ტალღა ორ კოჰერენტულ ტალღად უნდა გაიყოს და შემდეგ მათი შეკრების დაკვირვება ეკრანზე უნდა მოხდეს. ასე კეთდება ყველა ინტერფერენციულ სქემაში. მაგრამ ამ შემთხვევაშიც კი, ინტერფერენციული სურათი ქრება, თუ სვლათა Δ სხვაობა კოჰერენტულობის სიგრძეს cτ გადააჭარბებს.