ლინზას ორი სფერული ზედაპირით შემოსაზღვრულ გამჭვირვალე სხეულს უწოდებენ. თუ მისი სისქე მცირეა სფერული ზედაპირების სიმრუდის რადიუსთან შდარებით, მაშინ ლინზას თხელს უწოდებენ.
ლინზები პრაქტიკულად ყველა ოპტიკური ხელსაწყოს შემადგენმომაში შედიან. არსებობს შემკრები და გამბნევი ლინზები. შემკრები ლინზა შუაში უფრო სქელია ვიდრე კიდეებზე, გამბნევი კი პირიქით, შუაშია უფრო თხელი (ნახ. 1).
ნახ. 1.
შემკრები (a) და გამბნევი (b) ლინზები და მათი პირობითი აღნიშვნა
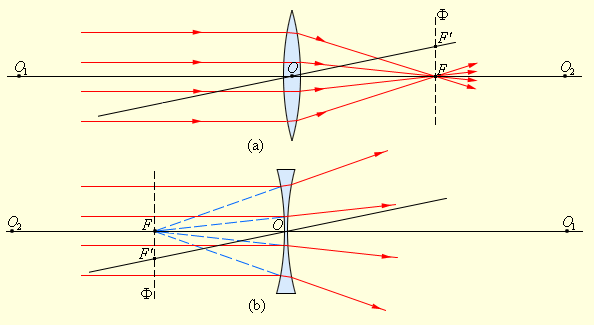
სწორს, რომელიც სიმრუდის O1 და O2 ცენტრებზე გადის, ლინზის მთავარი ოპტიკური ღერძი ეწოდება. თხელი ლინზის შემთხვევაში მიახლოებით შეიძლება ჩავთვალოთ, რომ მთავარი ოპტიკური ღერძი ლინზასთან მხოლოდ ერთ O წერტილში იკვეთება, რომელსაც ლინზის ოპტიკურ ცენტრს უწოდებენ. სინათლის სხივი ოპტიკუტ ცენტრზე გავლისას არ გადაიხრება საწყისი მიმართულებიდან. ოპტიკურ ცენტრზე გამავალი ყველა სწორს გვერდითი ოპტიკური ღერძები ეწოდება.
თუ ლინზაზე მთავარი ოპტიკური ღერძის სხივთა პარალელურ კონას მივმართავთ, ლინზაში გავლის შემდეგ სხივები (ან მათი გაგრძელებები) შეიკრიბებიან ერთ F წერტილში, რომელსაც ლინზის მთავარ ფოკუსს უწოდებენ. თხელ ლინზებს ორი მთავარი ფოკუსი აქვთ, რომლებით ლინზის ღერძის სიმეტრიულად არიან განლაგებული. შემკრები ლინზის ფოკუსი ნამდვილია, გამბნევისა კი - წარმოსახვითი. ერთ-ერთი გვერდითი ოპტიკური ღერძის პარალელური სხივთა კონა, ლინზაში გავლის შემდეგ ასევე ერთ F' წერტილში იყრის თავს, რომელიც გვერდითი ოპტიკური ღერძისა და ფოკალური Ф სიბრტყის გადაკვეთაზე მდებარეობს, ანუ მთავარ ოპტიკურ ფოკუსზე გამავალ მთავარი ოპტიკური ღერძის მართობულ სიბრტყეზე (ნახ. 2). ლინზის ოპტიკურ O ცენტრსა და მთავარ F ფოკუსს შორის მანძილს ფოკუსურ მანძილს უწოდებენ. ისიც F ასოთი აღინიშნება.
ნახ. 2.
პარალელურ სხივთა კონის გარდატეხა შემკრებ (a) და გამბნევ (b) ლინზებში. O1 და O2 წერტილები სფერული ზედაპირების ცენტრებია, O1O2 – მთავარი ოპტიკური ღერძი, O – ოპტილური ცენტრი, F– მთავარი ფოკუსი, F' – გვერდითი ფოკუსი, OF' – გვერდითი ოპტიკური ღერძი, Ф – ფოკალური სიბრტყე
ლინზის მთავარი თვისება საგნის გამოსახულების მოცემის უნარია.გამოსახულება შიუძლება იყოს პირდაპირი და გადაბრუნებული, ნამდვილი და წარმოსახვითი, გადიდებული და შემცირებული.
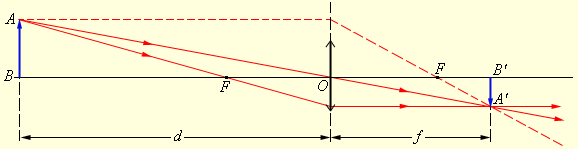
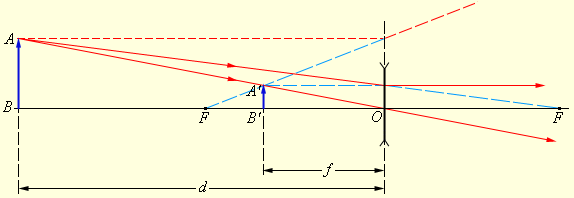
გამოსახულების მდებარეობა და მისი ხასიათი შეიძლება გეომეტრიული აგების საშუალებით დადგინდეს. ამისათვის გამოიყენება ზოგიერთი ისეთი სტანდარტული სხივის თვისება, რომელთა სვლაც ცნობილია. ეს სხივები გადიან ოპტუკირ ცენტრზე ან ლინზის ერთ-ერთ ფოკუსზე, და ასევე, პარალელურია მთავარი ოპტიკური ღერძისა ან ერთ-ერთ გვერდითი ოპტიკური ღერძის. ასედი აგების მაგალითები ნახ. 3 -სა და 4-ზეა მოცემული.
ნახ. 3.
გამოსახულების აგება შემკრებ ლინზაში
ნახ. 4.
გამოსახულების აგება გამბნევ ლინზაში
ყურადღება უადა მიექცეს იმას, რომ გამოსახულების ასაგებად ნახ.3-სა და 4-ზე გამოყენებული ზოგი სტანდარტული სხივი ლინზაში არ გადის. ეს სხივები გამოსახულების შექმნაში რეალურად არ მონაწილეობენ, მაგრამ აგებისთვის შესაძლებელია მათი გამოყენება.
გამოსახულების მდებარეობა და მისი ხასიათი (ნამდვილია თუ წარმოსახვითი) შეიძლება, აგრეთვე, თხელი ლინზის ფორმულით გაითვალოს. თუ სხეულიდან ლინზამდე მანძილს d -თი ავღნიშნავთ, ხოლო ლინზიდან გამოსახულებამდე f -ით, მაშინ თხელი ლინზის ფორმულა შეიძლება ასე ჩავწეროთ:
D სიდიდე ფოკუსური მანძილის შებრუნებულია და ლინზის ოპტიკურ ძალას უწოდებენ. ოპტიკური ძალის ერთეულია დიოპტრი. დიოპტრი ერთი მეტრი ფოკუსური მანძილის მქონე ლინზის ოპტიკური ძალაა:
1 დიოპტრი = მ–1
თხელი ლინზის ფორმულა სფერული ლინზის ფორმულის ანალოგიურია. იგი პარაქსიალური სხივებისთვის შეიძლება მივიღოთ ნახ. .3 ან 4-დან სამკუთხედების მსგავსებით.
ლინზების ფოკუსურ მანძილებს გარკვეულ ნიშანს ანიჭებენ: შემკრები ლინზისათვის F > 0, ხოლო გამბნევისათვის F < 0.
d და f სიდიდეები ასევე გარკვეულ ნიშანთა წესს ემორჩილებიან:
d > 0 და f > 0 – ნამდვილი საგნებისთვის (ე.ი. სინათლის რეალური წყაროებისათვის, და არა სხივების გაგრძელებებისათვის რომლებიც ლინზის მეორე მხარეს იკრიბებიან) და გამოსახულებებისთვის;
d < 0 და f < 0 – წარმოსახვითი საგნებისა და გამოსახულებისათვის.
ნახ. 3-ზე გამოსახული შემთხვევისთვის გვაქვს: F > 0 (შემკრები ლინზა), d = 3F > 0 (ნამდვილი საგანი).
თხელი ლინზის ფორმულის მიხედვით: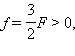 
ამიტომ, გამოსახულება ნამდვილია.
ნახ. 4-ზე გამოსახული შემთხვევისათვის გავქვს: F < 0 (გამბნევი ლინზა), d = 2|F| > 0 (წარმოსახვითი საგანი),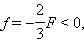 
ე.ი. გამოსახულება წარმოსახვითია.
საგნის ლინზის მიმართ მდებარეობაზე დამოკიდებულებით იცვლება გამოსახულების ზომები. ლინზის წრფივი გადიდება ეწოდება გამოსარულებისა h' და საგნის h წრფივი ზომების ფარდობას. h' სიდიდეს, ისევე როგორც სფერული სარკის შემთხვევაში, მოსახერხებელია მივუწეროთ პლიუსი ან მინუსი იმის მიხედვით, გამოსახულება პირდაპირია თუ გადაბრუნებული. h სიდიდე დადებითად ითვლება. ამიტომ პირდაპირი გამოსახულებებისთვის Γ > 0, გადაბრუნებულებისათვის Γ < 0. ნახ. 3 და 4-ზე სამკუთხედების მსგავსებიდან ადვილად მიიღება წრფივი გადიდების ფომულა თხელი ლინზისთვის:
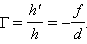
შემკრები ლინზის განხილულ მაგალითში (ნახ. 3.3.3): d = 3F > 0,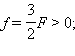 
აქედან გამომდინარე, 
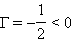– გამოსახულება გადაბრუნებულია და ორჯერ შემცირებული.
გამბნევი ლინზის შემთხვევაში (ნახ. 4): d = 2|F| > 0, 
; აქედან გამომდინარე,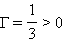 
– გამოსახულება პირდაპირია და სამჯერ შემცირებული.
ლინზის ოპტიკური ძალა D დამოკიდებილია მისი სფერული ზედაპირების სიმრუდის R1 და R2 რადიუსებზე და იმ მასალის გარდატეხის მაჩვენებელზე, რომლისგანაცაა ლინზა დამზადებული.
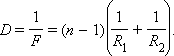
ამოზნექილი ზედაპირის სიმრუდის რადიუსი დადებითად ითვლება, ხოლო ჩაზნელილისა კი - უარყოფითად. ეს ფორმულა გარკვეული ოპტიკური ძალის ლინზის დასამზადებლად გამოიყენება.
მრავალ ოპტიკურ ხელსაწყოში სინათლე მიმდევრობით ორ ან რამდენიმე ლინზაში გადის. პირველი ლინზით მიღებული გამოსახულება მეორე ლინზისთვის საგანს (ნამდვილს ან წარმოსახვითს) წარმოადგენს, რომელიც მეორე ლინზის გამოსახულებას იძლევა. ეს მეორე გამოსახულებაც შეიძლება იყოს ნამდვილი ან წარმოსახვითი. ორ ლინზიანი სისტემის გათვლა დაიყვანება ლინზის ფორმულის ორმაგ გამოყენებაზე, ამასთან პირველი გამოსახულებიდან მეორემდე მანძილი d2 იყოს სიდიდის l – f1 ტოლი, სადაც l – ლინზებს შორის მანძილია. ლინზის ფორმულით გათვლისას f2 სიდიდე განსაზღვრავს მეორე გამოსახულების მდებარეობას და ხასიათს (f2 > 0 – ნამდვილი გამოსახულება, f2 < 0 – წარმოსახვითი). ორი ლინზისგან შემდგარი სისტემის სრული წრფივი გადიდება ორივე ლინზის წრფივ გადიდებათა ნამრავლის ტოლია: Γ = Γ1 · Γ2. თუ საგანი ან მისის გამოსახულება უსასრულობაში მდებარეობს, მაშინ წრფივი გადიდება აზრს კარგავს.
კერძო შემთხვევას ორი ლინზისგან შემდგარ ტელეკოპში სხივთა სვლა წარმოადგენს, როდესაც საგანიც და მეორე გამოსახულებაც უსასრულოდ დიდ მანძილზე მდებარეობენ. სხივთა ტელესკოპური სვლა რეალიზდება მაყურებლის მილებში – კოლერის ასტრონომიულ მილში და გალილეის დედამიწის მილში .
თხელ ლინზებს აქვთ გარკვეული ნაკლოვანებები, რომლებიც არ იძლევიან მაღალხარისხოვანი გამოსახულების მიღების საშუალებას. დამახინჯებებს, რომლებიც გამოსახულების ფორმირებისას მიიღება, აბერაციებს უწოდებენ. მათ შორის უნმიშვნელოვანესია სფერული და ქრომატული აბერაციები. სფერული აბერაცია ვლინდება იმაში, რომ სინათლის ფართო კონაში, ოპტიკური ღერძიდან დიდიდ დაშორებილი სხივები ფოკუსში არ იკვეთებიან. თხელი ლინზის ფორმულა სამართლიანია მხოლოდ ოპტიკური ღერძის მახლობელი სხივებისათვის. შორს მყოფი წერტილოვანი წყარის გამოსახულება, რომელის სხივთა ფართო კონით იქმნება, ლინზაში გავლის შემდეგ გადღაბნილი აღმოჩნდება.
ქრომატული აბერაცია იმითაა გამოწვეულია, რომ ლინზის მასალის გარდატეხის კოეფიციენტი სინათლის ტალღის λ სიგრძეზეა დამოლიდებული. გამჭვირვალე გარემოს ამ თვისებას დისპერსიას უწოდებენ. ლინზის ფოკუსური მანძილი სხვადასხვა ტალღის სიგრძის სინათლისათვის სხვადასხვაა, რასაც არამონოქრომატული ლინძების გამოყენების შმთხვევაში გამოსახულების გადღაბნასთან მივყავართ.
თანამედროვე ოპტიკურ ხელსაწყოებში თხელი ლინზების ნაცვლად, რთული მრავალლინზიანი სისტემები გამოიყენება, რომელებშიც სხვადასხვა აბერაციების გარკვეული მიახლოებით გასწორება ხდება შესაძლებელი.
შემკრები ლინზის საშუალებით ფორმირებული საგნის ნამდვილი გამონასახი მრავალ ოპტიკურ ხელსაწყოში გამოიყენება. მაგ., ფოტოაპარატში, პროექტორში და სხვა.
ფოტოაპარატი დახურული, სინათლეგაუმტარი კამერაა. გადასაღები საგნების გამოსახულება ფოტოფირზე (მიმღებზე) მიიღება ლინზების სისტემით, რომელსაც ობიექტივს უწოდებენ. სპეციალური ჩამკეტი საშუალებას იძლვა ობიექტივი გაიხსნას ექსპოზიციის შესაბამისი ხანგრძლივობით.
ფოტოაპარატის მუშაობის თავისებურება იმაში მდგომარეობს, რომ ბრტყელ მიმღებზე სხვადსხვა მანძილზე მდებარე საგნების საკმაოდ მკვეთრი (მკაფიო) გამოსახულება უნდაი ქნეს მიღებული.
მიმღების სიბრტყეში მკვეთრად მხოლოდ გარკვეულ მანძილზე მდებარე საგნების გამოსახულებები მიიღება. სიმკვეთრე ობიექტივის მიმღების სიბრტყის მიმართ გადაადგილებით მიიღწევა. იმ წერტილების გამოსახულებები, რომლებიც სიმკვეთრის სიბრტყეში არ მდებარეობენ, გაფანტული წრეების სახით იდღაბნება. ამ წრეების d დიამეტრის შემცირება შეიძლება დიაფრაგმირების საშუალებით, ე.ი. ფარდობითი ხვრელის a / F შემცირებით მიიღწეს (ნახ. 5). ამას სიმკვეთრის სიღრმის გადიდებასთან მივყავართ.
ნახ. 5.
ფოტოაპარატი
საპროექციო აპარატი მსხვილმაშტაბოვანი გამოსახულების მისაღებადაა განკუთვნილი. პროექტორის O ობიექტივი ბრტყელი საგნის (დიაპოზიტივიD) გამისახულებას დაშორებულ Э ეკრანზე აფოკუსებს (ნახ. 3.3.6). კონდენსორად წოდებულ ლინზათა K სისტემა S სინათლის წყაროს დიაპოზიტივზე კონცენტრირებისთვისაა განკუთვნილი. Э ეკრანზე ნამდვილი, გადიდებული, გადაბრუნებული გამისახულება მიიღება. საპროექციო აპარატის გადიდება შეიძლება შეიცვალის Э ეკრანის მიახლოებასა ან დაშორებასთან ერთად D დიაპოზიტივსა და O ობიექტივს შორის მანძილის ცვლით.
ნახ. 6.
საპროექციო აპარატი