თანამედროვე შეხედულებით ელექტრული მუხტები არ მოქმედებენ ერთმანეთზე უშუალოდ (შეხებით). ყოველი დამუხტული სხეული გარემომცველ სივრცეში ქმნის ელექტრულ ველს. ეს ველი ძალით მოქმედებს მეორე დამუხტულ სხეულზე. ელექტრული ველის ძირითადი თვისება ელექტრულ მუხტზე გარკვეული ძალით მოქმედებაში მდგომარეობს. ამგვარად, დამუხტული სხეულებს ურთიერთქმედება ხორციელდება არა მათი უშუალო ზემოქმედებით ერთმანეთზე, არამედ მათი გარემომცველი ელექტრული ველის საშუალებით.
დამუხტული სხეულის გარემომცველი ელექტრული ველის შესწავლა შესაძლებელია ე.წ. სასინჯი მუხტის საშუალებით, რომელიც სიდიდით მცირე წერტილოვან მუხტს წარმოადგენს და არ იწვევს გამოსაცდელი მუხტების საგრძნობ გადანაწილებას.
ელექტრული ველის რაოდენობრივი განსაზღვრისათვის შემოტანილია ძალითი მახასიათებელი - ელექტრული ველის დაძაბულობა.
ელექტრული ველის დაძაბულობა ეწოდება ფიზიკურ სიდიდეს, რომელიც ტოლია ველის მიერ სივრცის მოცემულ წერტილში მოთავსებულ დადებით საცდელ მუხტზე მოქმედი ძალის ფარდობისა ამ მუხტის სიდიდესთან:
\(\vec{E}=\frac{\vec{F}}{q}.\)
ელექტრული ველის დაძაბულობა ვექტორული ფიზიკური სიდიდეა. \(\vec{E}\) ვექტორის მიმართულება სივრცის ყოველ წერტილში ემთხვევა დადებით საცდელ მუხტზე მომქმედი ძალის მიმათულებას.
უძრავი და დროში უცვლელი მუხტების ელექტრულ ველებს ელექტროსტატიკური ეწოდება. ბევრ შემთხვევაში ამ ველის სახელს სიმოკლისათვის ზოგადი ტერმინით - ელექტრული ველით ცვლიან.
თუ საცდელი მუხტის საშუალებით იკვლევენ რამოდენიმე დამუხტული სხეულის მიერ შქმნილ ელექტრულ ველს, ტოლქმედი ძალა საცდელ მუხტზე თითოეული დამუხტული სხეულის მხრიდან მომქმედი ძალების გეომეტრიული ჯამის ტოლი გამოდის. აქედან გამომდინარე, მუხტების სისტემის მიერ სივრცის მოცემულ წერტილში შექმნილი ელექტრული ველის დაძაბულობა ამ მუხტების მიერ ამავე წერთილში ცალ-ცალკე შექმნილი ელექტრული ველის დაძაბულობების ვექტორული ჯამის ტოლია:
\(\vec{E}=\vec{E_{1}}+\vec{E_{2}}+....\)
ელექტრული ველის ამ თვისებას სუპერპოზიციის პრინციპს უწოდებენ.
კულონის კანონის თანახმად Q წერტილოვანი მუხტის მიერ მისგან r მანძილზე შექმნილი ელექტრული ველის დაძაბულობა მოდულით ტოლია:
\(E=\frac{1}{4\pi\varepsilon_{0}}\cdot\frac{Q}{r^{2}}.\)
ამ ველს კულონის ველს უწოდებენ. კულონის ველში \(\vec{E}\) ვექტორის მიმართულება Q მუხტის ნიშანზეა დამოკიდებული: თუ Q > 0, მაშინ \(\vec{E}\) ვექტორი მიმართულია რადიუსის გასწვრივ მუხტიდან, და თუ Q < 0,მაშინ \(\vec{E}\) ვექტორი მიმართულია მუხტისკენ.
ელექტრული ველის თვალსაჩინო წარმოდგენისათვის იყევებენ ძალწირებს. ისინი ისეა გატარებული, რომ \(\vec{E}\) ვექტორის მიმართულება ყოველ წერტილში ემთხვა ძალწირების მხებს (ნახ. 1). ელექტრული ველის ძალწირებით გამოსახვისას მათი სიხშირე დაძაბულობის ვექტორის მოდულის პროპორციული უნდა იყოს.

ნახ. 1.
ელექტრული ველის ძალწირები.
დადებითი და უარყოფითი წერტილოვანი მუხტების კულონის ველის ძალხაზები გამოსახულია ნახ. 2-ზე. რადგანაც მუხტების ნებისმიერი სისტემის მიერ შექმნილი ელექტროსტატიკური ველი შეიძლება წარმოვადგინოთ, როგორც წერტილოვანი მუხტების კულონის ველების სუპერპოზიცია, ნახ. 2-ზე გამოსახული ველები შეიძლება განვიხილოთ, როგორც ნებისმიერი ველის ელემენტარული სტრუქტურურლი ერთეულები („აგურები“).
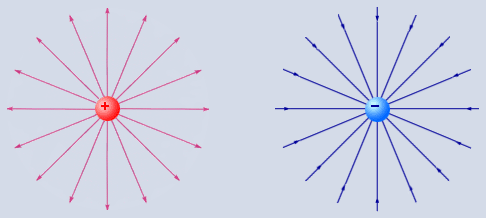
ნახ. 2.
კულონის ველების ძალწირები.
Q წერტილოვანი მუხტის კულონის ველი მოსახერხებელია ჩაიწეროს ვექტორული სახით. ამისათვის უნდა გავავლოთ \(\vec{r}\) რადიუს-ვექტორი Q მუტიდან დაკვირვების წერტილისაკენ. მაშინ, როცა Q > 0, \(\vec{E}\) ვექტორი პარალელურია \(\vec{r}\)-ს, ხოლო Q < 0, მაშინ \(\vec{E}\) ვექტორი ანტიპარალელურია \(\vec{r}\)-ს. ე.ი. შეიძლება ჩაიწეროს:
\(\vec{E}=\frac{1}{4\pi\varepsilon_{0}}\cdot\frac{Q}{r^{3}}\vec{r},\)
სადაც r - \(\vec{r}\) რადიუს-ვექტორის მოდულია.
ველების სუპერპოზიციის პრინციპის მაგალითად ნახ. 3-ზე გამოსახულია ელექტრული დიპოლის - ერთმანეთისაგან l მანძილზე განლაგებული ორი მოდულით ტოლი და სხვადასხვა ნიშნიანი q და –q მუხტების სისტემის, ძალწირები.

ნახ. 3.
დიპოლის ელექტრული ველის ძალხაზები \(\vec{E}=\vec{E_{1}}+\vec{E_{2}}.\)
ელექრტული დიპოლის მნიშვნელოვან მახასიათებელს წარმოადგენს ე.წ. დიპოლური მომენტი \(\vec{p}\):
\(\vec{p}=\vec{l}q,\)
სადაც \(\vec{l}\) - უარყოფითი მუხტიდან დადებითისაკენ მიმართული ვექტორია, მოდულით \(|\vec{l}|=l.\) . დიპოლი შეიძლება მრავალი მოლეკულის ელექტრულ მოდელად იქნეს გამოყენებული.
ელექტრული დიპოლს აქვს მომენტი, მაგალითად, წყლის ნეიტრალურ მოლეკულას (H2O), რადგანაც წყალბადის ორი ატომის ცენტრები განლაგებული არ არის ერთ სწორ ხაზზე ჟანგაბაგის მოლეკულის ცენტრთან, არამედ 105° გარადუსიანი კუთხით (ნახ. 4). წყლის მოლეკულის დიპოლური მომენტი p = 6,2·10–30 კალ · მ.

ნახ. 4.
წყლის მოლეკულის დიპოლური მომენტი
ელექტროსტატიკის მრავალ ამოცანეში საჭიროა მუხტაბის გარკვეული განაწილებისათვის (განლაგებისათვის) განისაზღვროს \(\vec{E}\) ელექტრულლი ველი. ვთქვათ, მაგალითად, საჭიროა გრძელი ერთგვაროვნად დამუხტული ძაფის ელექტრული ველის პოვნა (ნახ. 5) მისგან R მანძილზე.
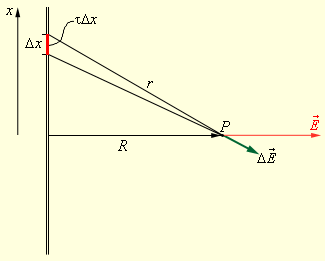
ნახ. 5.
დამუხტული ძაფის ელექტრული ველი
P დაკვირვების წერტილში ველი შეიძლება წარმოვადგინოთ ძაფის მცირე Δx ელემენტების კულონის ძალების სუპერპოზიციის სახით, რომელთა მუხტები τΔx-ის ტოლია, სადაც τ - ძაფის სიგრძის ერთეულის მუხტია. ამოცანა დაიყვანება ელემენტარული \(\Delta\vec{E}\) ველების აჯამვაზე (ინტეგრირებაზე). ველის ტოლქმედი ტოლია
\(E=\frac{\tau}{2\pi\varepsilon_{0}R}.\)
\(\vec{E}\) ვექტორი ყველგან მიმართულია \(\vec{R}\) რადიუსის გასწვრივ. ეს ამოცანის სიმეტრიიდან გამომდინარეობს. უკვე ეს მარტივი მაგალითი გვიჩვენებს, რომ მუხტების მოცემული განაწილებისას ველის განსაზღვრის პირდაპირ გზას მივყავართ რთულ მათემატუკურ გათვლებთან. გაუსის თეორემის გამოყენებით, რომელიც ელექტრული ველის ფუნდამენტურ თვისებას გამოსახავს, ზოგიერთ შემთხვევაში შეიძლება საგრძნობლად გავამარტივოთ გამოთვლები.


