• დრეკადი და არადრეკადი შეჯახებები
• მყარი სხეულის ბრუნვა

სითხეებისა და აირების მოძრაობა რთულ მოვლენას წარმოადგენს. მისი აღწერისათვის სხვადასხვა გამარტივებული დაშვება (მოდელი) გამოიყენება. უმარტივეს მოდელში, სითხე (და აირიც კი) უკუმშვადად და იდეალურადაა (ე.ი.მოძრაობისას ფენებს შორის შინაგანი ხახუნი არ არის) მიღებული. იდეალური სითხის მოძრაობისას მექანიკური ენერგიის შინაგან ენერგიად გარდაქმნა არ ხდება, ამიტომ ადგილი აქვს მექანიკური ენერგიის მუდმივობის კანონს. ამ კანონის შედეგს, იდეალური და უკუმშვადი სითხის სტაციონალური ნაკადისათვის, 1738 წელს ჩამოყალიბებული ბერნულის განტოლება წარმოადგენს. სტაციონალურად უწოდებენ ისეთი სითხის ნაკადს, რომელშიც გრიგლები არ წარმოიქმნება.  სტაციონალურ ნაკადში სითხის ნაწილაკები გადაადგილდებიან დროში უცვლელი ტრაექტორიებით, რომელთაც დენის წირები ეწოდებათ. გამოცდილება გვიჩვენებს, რომ სტაციონალური ნაკადები მხოლოდ სითხის მცირე სიჩქარით მოძრაობისას წარმოიქმნება.

 

განვიხილოდ იდეალური   და უკუმშვადი სითხის სტაციონალური ნაკადის მოძრაობა ცვლადი განივკვეთის მილში (ნახ. 1). მილის სხვადასხვა ნაწილები სხვადასხვა სიმაღლეზე შეიძლება იყოს განლაგებული.

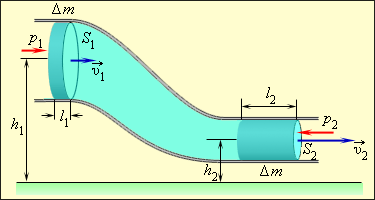
ნახ. 1.

ცვლადი განივკვეთის მილში იდეალური სითხის დენა.

 \(\Delta V_{1}=l_{1}S_{1}; \Delta V_{2}=l_{2}S_{2}\).

უკუმშვადობის პირობა: \(\Delta V_{1}=\Delta V_{2}=\Delta V\) დროის \(\Delta t\) მონაკვეთში  \(S_{1}\) განივკვეთის მილში სითხე გადანაცვლდება \(l_{1}=u_{1}\Delta t\) –ზე, ხოლო \(S_{2}\) განივკვეთის მილში –  \(l_{2}=u_{2}\Delta t\) –ზე, სადაც \(v_{1}\) და \(v_{2}\) – მილში სითხის ნაწილაკების სიჩქარეა. უკუმშვადობის პირობა  ჩაიწერება შემდეგი სახით: 

\(\Delta V=l_{1}S_{1}=l_{2}S_{2}\)    ან    \(v_{1}S_{1}=v_{2}S_{2}\) .

სადაც \(\Delta V\) – \(S_{1}\) და \(S_{2}\) –ში გამდინარე სითხის მოცულობაა.

ამგვარად, სითხის, დიდი განივკვეთის მქონე მილიდან ნაკლები განივკვეთის მილში, გადასვლისას დინების სიჩქარე იზრდება, ე.ი. სითხე აჩქარებულად მოძრაობს. აქედან გამომდინარე, სითხეზე ძალა მოქმედებს. ჰორიზონტულ მილში ეს ძალა მხოლოდ ფართო და ვიწრო მილებში  წნევათა სხნაობის გამო შეიძლება აღიძრას. თუ მილის ეს მონაკვეთები სხვადასხვა დონეზე მდებარეობენ, მაშინ აჩქარება გამოწვეულია  წნევისა და სიმძიმის ძალების ერთდროული მოქმედებით. წნევის ძალა – სითხის შეკუმშვის დრეკადობის ძალაა. სითხის უკუმშვადობა მხოლოდ იმას ნიშნავს, რომ დრეკადობის ძალები თავს იჩენს მხოლოდ სითხის ნებისმიერი ნაწილის მოცულობის იმდენად მცირე ცვლილევისას, რომ მისი უგულვებელყოფა შეიძლება.

რადგან სითხე იდეალურადაა ჩათვლილი, ის მილში ხახუნის გარეშე მიედინება. ამიტომ მის დინებასთან შეიძლება მექანილური ენერგიის მუდმივობის კანონის მიყენება.

სითხის გადაადგილებისას წნევის ძალები ასრულებენ მუშაობას:

\(\Delta A=p_{1}S_{1}l_{1}-p_{2}S_{2}l_{2}=p_{1}S_{1}v_{1}\Delta t-p_{2}S_{2}v_{2}\Delta t=(p_1-p_{2})\Delta V.\) 

წნევის ძალების მუშაობა ΔA სითხის დრეკადი დეფორმაციის პოტენციური ენერგიის ცვლილების ტოლია საწინააღმდეგო ნიშნით.

დროის საწყისი მომენტიდან \(S_{1}\) და \(S_{2}\) შორის მოქცეულ სითხეში \(\Delta t\) დროის განმავლობაში მომხდარი ცვლილებები, სტაციონალური დინებისას დაიყვანება  \(m=\rho \Delta V\) (\(\rho\) – სითხის სიმკვრივეა) მასის სითხის  მილის ერთი  \(S_{1}\) განივკვეთის მქონე ნაწილიდან მეორე \(S_{2}\) განივკვეთის მქონე ნაწილში გადაადგილებამდე (ნახ. 1–ზე დაშტრიხული მოცულიბა). ამ მასისათვის მექანიკური ენერგიის შენახვის კანონს აქვს სახე:

\(E_{2}-E_{1}=\Delta A=(p_{1}-p_{2})\Delta V,\) 

სადაც \(E_{1}\) და \(E_{2}\) –  მიზიდულობის ველში \(\Delta m\) მასის სრული მექანიკური ენერგიაა:

\(E_{1}=\frac{\Delta mv_{1}^{2}}{2}+\Delta mgh_{1}; E_{2}=\frac{mv_{2}^{2}}{2}+\Delta mgh_{2}.\) 

აქედან გამოდის:

\(\frac{\rho v_{1}^{2}}{2}+\rho gh_{1}+p_{1}=\frac{\rho v_{2}^{2}}{2}+\rho gh_{2}+p_{2}.\) 

სწორედ ეს არის ბერნულის განტოლება. აქედან გამოდის, რომ ჯამი მილის მთელი სიგრძის გასწვრივ მუდმივი რჩება:

\(\frac{\rho v^{2}}{2}+\rho gh+p=const.\)

კერძოდ, ჰორიზონტულად განლაგებული მილისათვის  (\(h_{1}=h_{2}\)  ბერნულის განტოლებას აქვს სახე:

\(\frac{\rho v^{2}}{2}+p=const.\) 

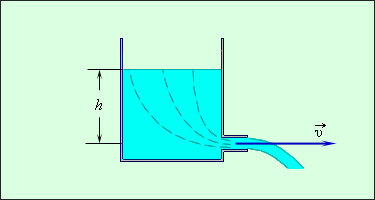
\(P\) სიდიდე – სითხეში სტატიკური წნევაა. ის შეიძლება სითხესთან ერთად მოძრავი მონომეტრის საშუალებით გაიზომოს. პრაქტიკულად წნევა, მილის სხვადასხვა განივკვეთში იზომება მონომეტრული მილების საშუალებით როგორც ნახ. 2–ზეა  ნაჩვენები. ბერნულის განტოლებიდან გამოდის, რომ:

ცვლადი განივკვეთის მქონე ჰორიზონტულ მილში გამდინარე სითხის წნევა იმ კვეთაშია მეტი, სადაც მოძრაობის (დინების) სიჩქარე ნაკლებია, და პირიქით, წნევა ისეთ კვეთაშია ნაკლები, სადავ სიჩქარე მეტია.

ნახ. 2.

სითხეში წნევის გაზომვა მონომეტრების საშუალებით. \(v_{1}<v_{2}<v_{3};\: h_{1}>h_{2}>h_{3}\) 

თუ სითხის ნაკადის კვეთა საკმარისად დიდია, ბერნულის განტოლება უნდა გამოვიყენით დენის წირებისათვის, ე.ი. წირებისათვის რომლის გასწვრივაც გადაადგილდება სითხის ნაწილაკები სტაციონალურო დინებისას. მაგალითად, იდეალირი უკუმშავადი სითხის განიერი ჭურჭლის გვერდითი კედლის  ან ფსკერის ნახვრეტიდან გამოდინებისას, დენის წირები იწყებიან ჭურჭლის ზედაპირთან და გადიან ნახვრეტში (ნახ. 3).

ნახ. 3,

სითხის გამოდინება განიერი ჭურჭლიდან

რადგან, ჭურჭლის ზედაპირთან  სითხის სიჩქარის უგულვებელოფა შეიძლება მისი სიმცირის გამო, ბერნულის განტოლება იღებს სახეს:

\(\rho gh+p_{0}=\frac{\rho v^{2}}{2}+p_{0},\) 

სადაც \(p_0\) – ატმოსფეროლი წნევაა, \(h\) – სითხის დინების მიმართ დონეთა სხვაობაა. ამგვარად,

\(v=\sqrt{2gh}.\) 

გამოდინების სიჩქარის ამ გამოსახულებას ტორიჩელის ფორმულას უწოდებენ. იდეალური სითხის ჭურჭლის ხვრელიდან გამოდინების სიჩქარე ისეთივეა როგორიც \(h\) სიმაღლიდან უსაწყისო სიჩქარით ვარდნილი სხეულის სიჩქარე.

სითხეებისაგან განსხვავებით აირებს შეუძლიათ მოცულებების მნიშვნელოვანი ცვილება. გათვლები უჩვენებენ, რომ აირების კუმშვადობის უგულვებელყოფა შესაძლებელია, თუ აირის ნაკადის უდიდესი სიჩქარე ნაკლებია, ამ აირში ბგერის გავრცელების სიჩქარეზე. ასეთ პირობებში, ბერნულის განტოლება  აეროდინამიკის ამოცანების ფართო კლასისათვის შეიძლება იქნეს გამოყენებული.

  

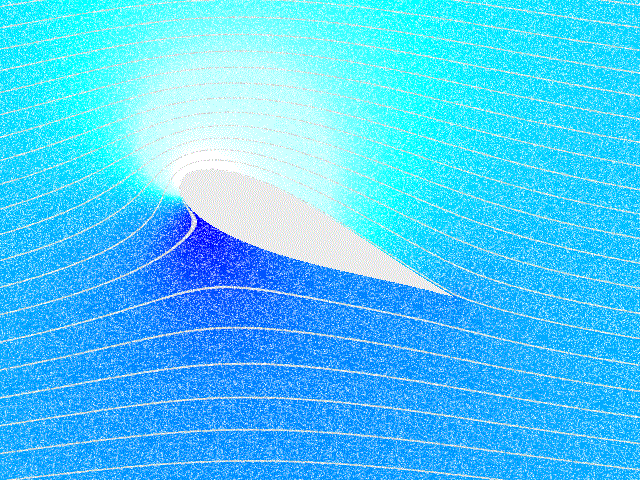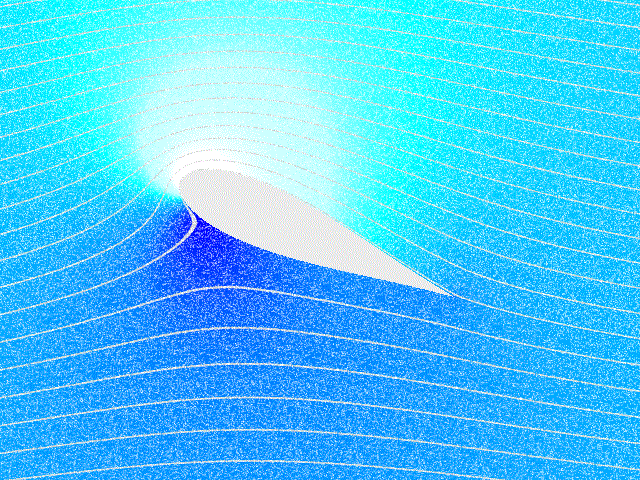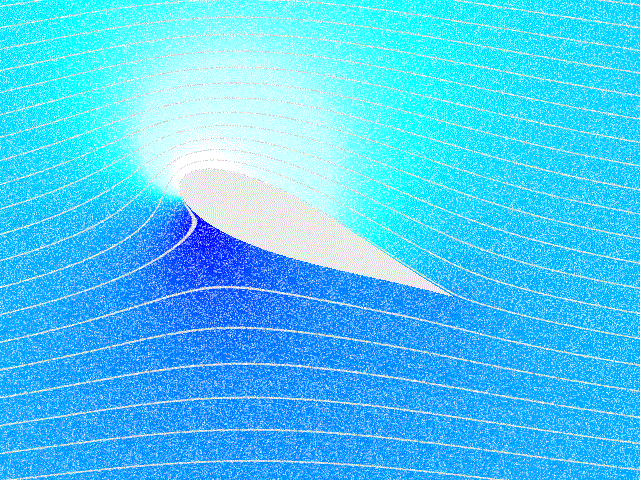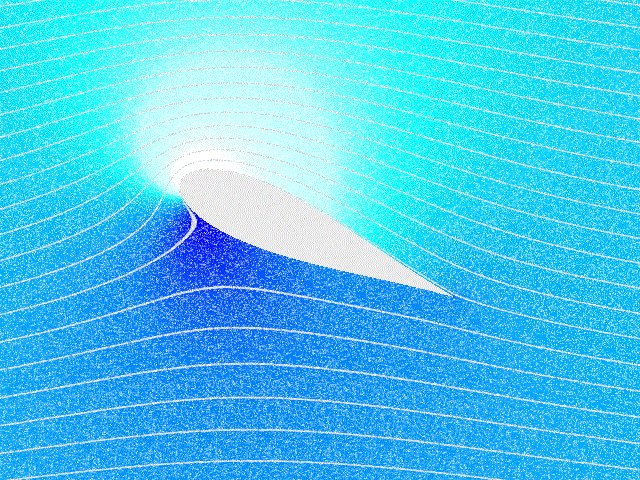
ერთ–ერთი ასეთი ამოცანაა თვითმფრინავის ფრთაზე მოქმედი ძალების შესწავლა. ამ ამოცანის მკაცრი თეორიული ამოხსნა ძალიან რთულია და ჩვეულებრივ, ძალების კვლევისათვის ექსპერიმენტულ მეთოდებს იყენებენ. ბერნულის განტოლება ფრთის ამწევი ძალის წარმოქმნის მხოლოდ რაოდენობრივი ახსნის საშუალებას იძლევა. ნახ. 4–ზე გამოსახულია თვითმფრინავის ფრთის გარსმდენი ჰაერის ნაკადის დინების წირები. ფრთის სპეციალური ფორმის და დაჯახების (ჰაერის დარტყმის) კუთხის, ე.ი. ფრთის დახრასა და მასზე დაცემული ჰაერის ნაკადს შორის კუთხის გამო ფრთის ზევით ჰაერის ნაკადის სიჩქარე უფრო მეტია ვიდრე ფრთის ქვევით. ამიტომ ნახ. 4–ზე დინების წირები ფრთის ზევით უფრო მჭიდროდაა (ახლო–ახლოა ერთმანეთთან) განლაგებული, ვიდრე ფრთის ქვევით. ბერნულის განტოლებიდან გამოდის, ფრთის ქვევით წნევა იქნება მეტი, ვიდრე ზევით; რის შედეგადაც აღიძვრება ფრთაზე მოქმედი ძალა \(\vec{F},\)  ამ ძალის ვერტიკალურ მდგენელს \(\vec{F}_{y}\) tამწევ ძალას უწოდებენ. ამწევი ძალა თვითმფრინავზე მოქმედი სიმძიმის ძალის კომპენსირების საშუალებას იძლევა და ამის მეშვეობით ჰაერში მძიმე საფრენი აპარატების ფრენაა შესაძლებელი. ჰორიზონტული მდგენელი \(\vec{F}_{x}\) გარემოს წინააღმდეგობის მდგენელს წარმოადგენს.

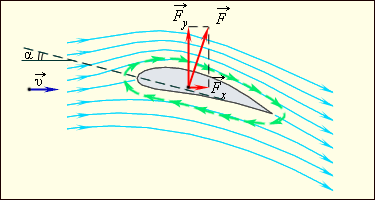
ნახ. 4.

თვითმფრინავის ფრთის გასმდენი ჰაერის  ნაკადის დინების წირები და ამწევი ძალის წარმოქმნა. \(\alpha\) –  დაჯახების კუთხე.

 

ფრთის ამწევი ძალის თეორიის მიხედვით ფრთის გარსშემოდინების დროს მნიშვნელოვან როლს ასრულებს ზედაპირულ ფენებში აღძრული სველი ხახუნის ძალები. მათი მოქმედების შედეგად ფრთის გარშემო აღიძვრება ჰაერის წრიული მოძრაობა (ცირკულაცია) (ნახ. 4–ზე მწვანე ისრები). ფრთის ზედა მაწილში ცირკულირებადი ჰაერის სიჩქარე იკრიბება ფრთაზე დაცემული ნაკადის სიჩქარესთან, ქვედა ნაწილში კი სიჩქარეები ურთიერთსაწინააღმდეგოდაა მიმართული. სწორედ ეს იწვევს წნევათა სხვაობას და ამწევი ძალის წარმოქმნას.

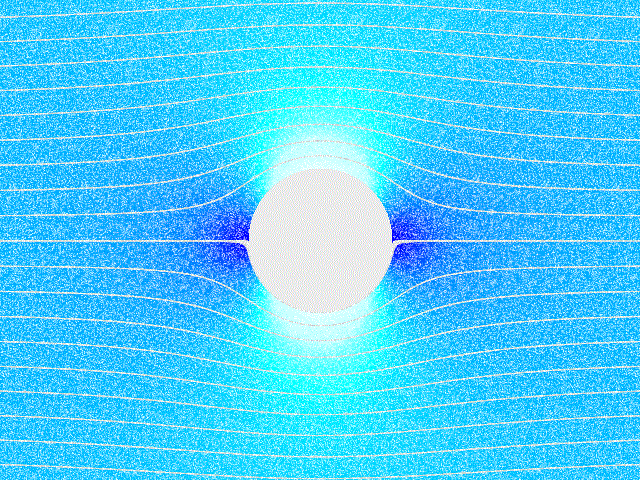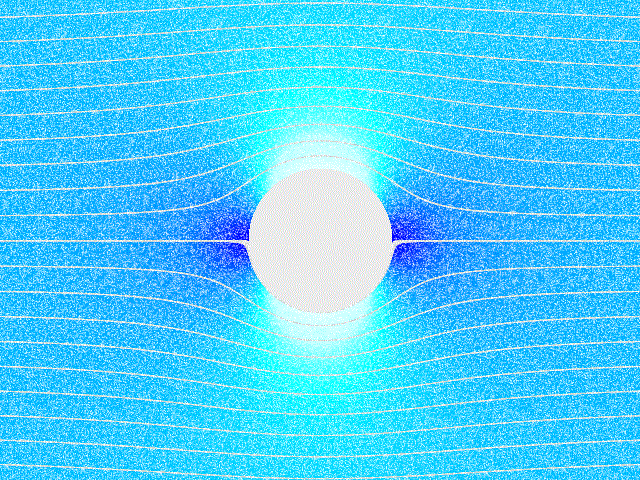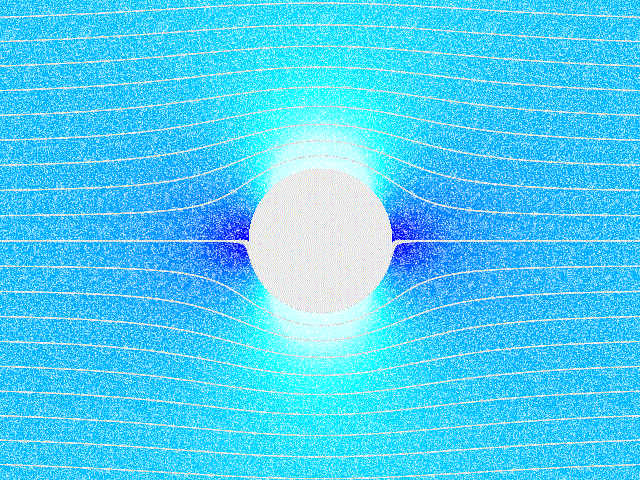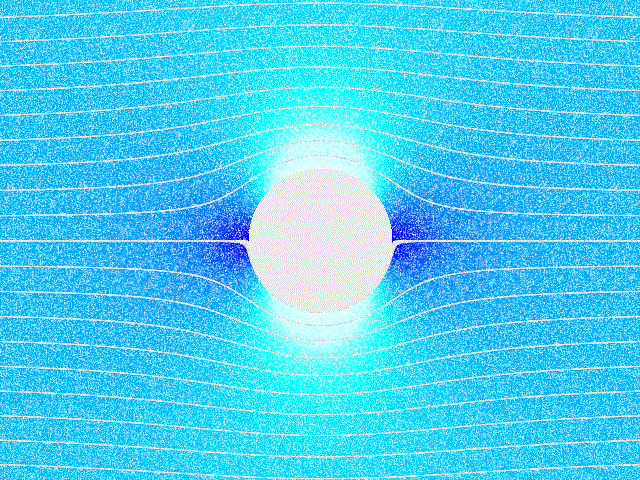
სველი ხახუნით გამოწვეული ჰაერის ცირკულაცია მბრუნავი სხეულის (მაგ. ცილინრის) გარშემოც აღიძვრება. ბრუნვისას, ცილინდრი აიყოლიებს გარშემო მყოფ ჰაერის ფენებს და  მათ ცირკულირებას იწვევს. თუ ასეთ ცილინდრს მოვათავსებთ ჰაერის ნაკადში, წარმოიქმნება, თვითმფრინავის ფრთის ამწევი ძალი ანალოგიური, გვერდითი წნევის ძალა. ამ მოვლენას მაგნუსის ეფექტს უწოდებენ. ნახ. 5–ზე ნაჩვენებია ჰაერის ნაკადში მოთავსებული მბრუნავი ცილინდრის გარშემოდენა. მაგნუსის ეფექტი წარმოიქმნება, მაგალითად, ტენისის ან ფეხბურთის ჩახვეულად მიწოდებული ბურთის ფრენისას.

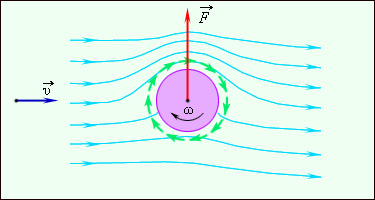
ნახ. 5.

ჰაერის ნაკადში მოთავსებული მბრუნავი ცილინდრის გარშემოდენა.

 

ასე რომ, სველი ხახუნის ძალები მნიშვნელოვან როლს ასრულებს აეროდინამიკის მრავალ მოვლენაში. ისინი იწვევენ თვითმფრინავის ფრთის ან მბრუნავი სხეულის გარშემო ჰაერის ცირკულირებადი ნაკადის შექმნას, გარემოს წინააღმდეგობის ძალების აღძვრას და ა.შ. ბერნულის განტოლება ხახუნის ძალებს არ ითვალისწინებს. მისი დასკვნები დაფუძვნებულია სითხისა და აირების დინებისა მექანიკური ენერგიის მუდმივობაზე. ამიტომაც, ბერნულის განტოვების საშუალებით შეუძლებელია ამომწურავი ახსნა იმ მოვლევებისა, სადაც   ხახუნის ძალები იჩენენ თავს. ასეთ შემთხვევებში შეიძლება მხოლოდ ხარისხობრივი მოსაზრებებით ვიხელმძღვანელოთ - რაც მეტია სიჩქარე აირის ნაკადში, მით ნაკლებია წნევა.

სველი ხახუნის ძალები განსაკუთრებით შესამჩნევად ვლინდება სითხის დინების დროს. ზოგი სითხის სიბლანტე იმდენად დიდია, რომ ბერნულის განტოლების გამოყენებამ შეიძლება ხარისხობრივად ძალინ განსხვავებულ, არასწორ შედეგებამდე მიგვიყვანოს. მადალითად, ბლანტი სითხის ჭურჭკის ხვრელიდან გამოდინებისას, ბერნულის განტოლებით გამოთვლილი მისი სიჩქარე შეიძლება ათეულობითჯერ ნაკლები იყოს ტორიჩელის ფომულით გამოთვლილთან შედარებით. სფერული სხეული იდეალურ სითხეში მოძრაობისას არ უნდა განიცდიდეს არანაირ წინააღმდეგობას. თუ ასეთ სხეული ბლანტ სითხეში მოძრაობს, აღიძვრება წინააღმდეგობის ძალა, რომლის სიდიდე მოძრაობის სიჩქარის \(v\) და სფეროს რადიუსის \(r\) პროპორციულია (სტოქსის კანონი).

\(F_{winaag}\sim v\cdot r.\) 

ამ ფორმულაში პროპორციულობის კოეფიციენტი სითხის თვისებებზეა დამოკიდებული.

ამიტომ, თუ მძიმე ბურთულას ბლანტი სითხით (მაგ. გლიცერინით) სავსე მაღალ ჭურჭელში ჩავაგდებთ, გარკვეული დროის შემდე ბურთულის სიჩქარე მიაღწევს გარკვეული სტაბულურ სიჩქარეს, რომელიც შემდგომი მოძრაობის მანძილზე არ შეიცვლება. ამ სტაბილური სიჩქარით მოძრაობისას ბურთულაზე მოქმედი ძალები (სიმძიმის ძალა \(m\vec{g},\) ამომგდები ძალა \(\vec{F}_{A}\) და გარემოს წინააღმდეგობის ძალა \(\vec{F}_{winaag}\)) კომპენსირებულია (გაწონასწორებილია), და მათი ტოლქმედი ნულის ტოლია.