მექანიკური ენერგიის და იმპულსის შენახვის კანონები ისეთი ამოცანების ამოხსნის საშუალებას იძლევა, რომლებშიც მომქმედი ძალები ცნობილი არ არის. ამგვარი ამოცანის მაგალითი სხეულების დარტყმითი ურთიერთქმედებაა.
სხეულების დარტყმითი ურთიერთქმედებასთან საქმე შეიძლება ხშირად გვქონდეს ყოველდღიურ ცხოვრებაში, ტექნიკასა და ფიზიკაში (განსაკუთრებით ატომებისა ელემენტარული ნაწილაკების ფიზიკაში).
დარტყმა (ან შეჯახება ) მიღებულია ვუწოდოთ სხეულების ხანმოკლე ურთიერთქმედებას, რომლის შედეგადაც მათი სიჩქარეები მნიშვნელონად იცვლება. შეჯახებისას სხეულებს შორის მოქმედებს ხანმოკლე დარტყმითი ძალები, რომელთა სიდიდეები, როგორც წესი, უცნობია. ამიტომ დარტყმითი ურთიერთქმედების განხილვა უშუალოდ ნიუტონის კანონების გამოყენებით შეუძლებელია. მექანიკური ენერგიისა და იმპულსის შენახვის კანონები გამოყენება, ბევრ შემთხვევაში, საშუალებას იძლევა განხილვიდან გამოვრიცხოთ თვით შეჯახების პროცესი და სიჩქარეების ყველა სხვა შუალედური მნიშვნელობის გამოტოვებით, მივიღოთ კავშირი სხეულების საწყის და საბოლოო სიჩქარეებს შორის.
მაქანიკაში ხშირად გამოიყენება დარტყმითი ურთიერთქმედების ორი მოდელი – აბსოლუტურად დრეკადი და აბსოლუტურად არადრეკადი დარტყმები.
აბსოლუტურად არადრეკადი დარტყმისას მექანიკური ენერგია არ ინახება. იგი სრულად ან ნაწილობრივ გადადის სხეულის შინაგან ენერგიაში (გათბობა).
აბსოლუტურად არადრეკადი დარტყმის მაგალითად გამოდგება ბალისტიკურ ქანქარასთვის ტყვიის (ან ჭურვის) მორტყმა. ბალისტიკური ქანქარა \(M\) მასის ქვიშით სავსე, ბაწარზე დაკიდებული ყუთია (ნახ. 1). \(\vec{v}\) სიჩქარით მოძრავი \(m\) მასის ტყვია ხვდება ყუთს და რჩება მასში. ქანქარის გადახრის საშუალებით სეიძლება ტყვიის სიჩქარის გამოთვლა.
ყუთის სიჩქარე მასში ჩარჩენილ ტყვიასთან ერთად ავღნიშნოთ \(\vec{u}\) –თი. მაშინ, იმპულსის შენახვის კანონის მიხედვით
\(mv=(M+m)u;\: u=\frac{m}{M+m}v.\)
ტყვიის ყუთში ჩარჩენისას მოხდა მექნიკური ენერგიის დაკარგვა:
\(\Delta E=\frac{mv^{2}}{2}-\frac{(M+m)u^{2}}{2}=\frac{M}{M+m}\frac{mv^{2}}{2}.\)
ფარდობა \(\frac{M}{M+m}\) –ტყვიის მექნიკური ენერგიის შინაგან ენერგიად გარდაქმნილი ნაწილია.
\(\frac{\Delta E}{E_{0}}=\frac{M}{M+m}=\frac{1}{1+\frac{m}{M}}.\)
ეს ფორმულა სამართლიანია არა მხოლოს ბალისტიკური ქანქარისათვის, არამედ ორი სხვადასხვა მასის სხეულის ნებისმიერი არადრეკადი შეჯახების შემთხვევაში.
როცა \(m<<M\), \(\frac{\Delta E}{E_{0}}\rightarrow 1\) ტყვიის კინეტიკური ენერგია თითქმის მთლიანად გარდაიქმნება შინაგან ენერგიად. როცა \(m=M\), \(\frac{\Delta E}{E_{0}}\rightarrow \frac{1}{2}\) – შინაგან ენერგიად გარდაიქმნება ტყვიის საწყისი კინეტიკური ენერგიის ნახევარი. და ბოლოს, დიდი მასის მოძრავი სხეულის მცირე მასის უძრავ სხეულთან (\(m>>M\)) არადრეკადი შეჯახებისას ფარდობა \(\frac{\Delta E}{E_{0}}\rightarrow 0.\)
ქანქარის შემდგომი მოძრაობა შეიძლება გამოვთვალოთ ენერგიის შენახვის კანონის საშუალებით:
\(\frac{(M+m)u^{2}}{2}=(M+m)gh;\: u^{2}=2gh,\)
სადაც \(h\)– ქანქარის გადახრის მაქსიმალირი სიმაღლეა. ამ ფორმულებიდან გამოდის:
\(v=\frac{M+m}{m}\sqrt{2gh}.\)
ცდით საშუალებით \(h\) სიმაღლის გაზომვით, შეიძლება განისაზღვროს ტყვიის \(v\) სიჩქარე.
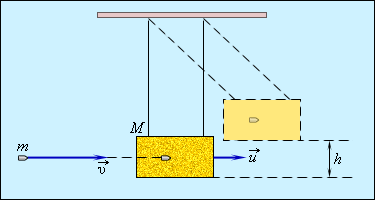
ნახ. 1.
ბალისტიკური ქანქარა
აბსოლუტურად დრეკად დარტყმას უწოდებენ შეჯახებას, რომლის დროსაც ინახება მექანიკური ენერგია.
ბევრ შემთხვევაში ატომების, მოლეკულების და ელემენტარული ნაწილაკების შეჯახება აბსოლურურად დრეკადი დარტყმის კანონებს ემორჩილება.
აბსოლურურად დრეკადი დარტყმის იმპულსის შენახვის კანონთან ერთად მექანიკური ენერგიის კანონიც სრულდება.
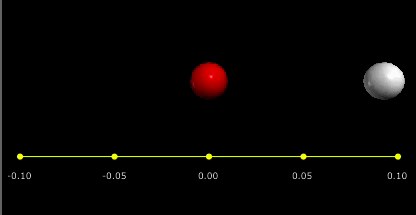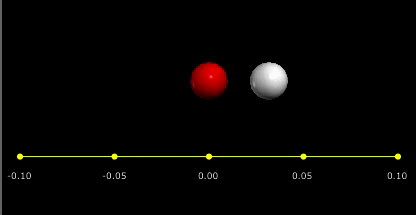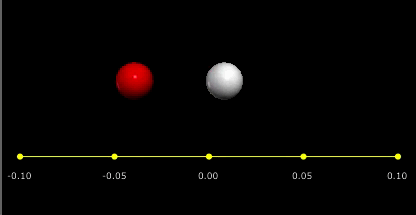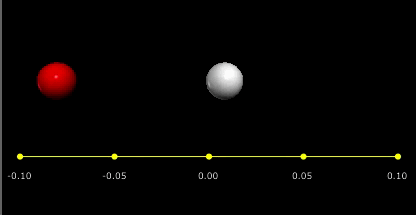
აბსოლურურად დრეკადი დარტყმის უბრალო მაგალითს ბილიარდის ორი ბურთულის ცენტრალური დარტყმა წარმოადგენს, როცა ერთ–ერთი მათგანი უძრავია (ნახ. 2).
ბურთულების ცენტრალურ დარტყმას ისეთ შეჯახებას უწოდებე, როცა ბურთულების სიჩქარეები დარტყმამდე და დარტყმის შემდეგ ცენტრებზე გამავალი წრფის გასწვრივაა მიმართული.

ნახ. 2.
აბსოლურურად დრეკადი ცენტრალურ დარტყმა
ზოგად შემთხვევაში შეჯახებაში მონაწილე ბურთულების მასები \(m_{1}\) და \(m_{2}\) შეიძლემა არ იყოს ერთნაირი. მექანიკური ენერგიის შენახვის კანონის თანახმად
\(\frac{m_{1}v_{1}^{2}}{2}=\frac{m_{1}u_{1}^{2}}{2}+\frac{m_{2}u_{2}^2}{2}.\)
სადაც \(v_{1}\) – პირველი ბურთულის სიჩქარეა შეჯახებამდე, მეორე ბურთულისთვის სიჩქარე \(v_{2}=0\), \(v_{1}\) და \(v_{2}\) – სიჩქარეები დაჯახების შემდეგ. იმპულსის შენახვის კანონი სიჩქარის გეგმილებში ღერძზე, რომელიც მოძრავი ბურთულის შეჯახებამდე სიჩქარის გასწვრივაა მიმართული, ასე ჩაიწერება:
\(m_{1}v_{1}=m_{1}u_{1}+m_{2}u_{2}\).
მივიღეთ განტოლებათა სისტემა. ამ სისტემის ამოხსნით ვიპოვით უცნობ \(u_{1}\) და \(u_{2}\) სიჩქარეებს
\(u_{1}=\frac{(m_{1}-m_{2})v_{1}}{m_{1}+m_{2}};\: u_{2}=\frac{2m_{1}v_{1}}{m_{1}+m_{2}}.\)
კერძო შემთხვევაში, როცა ორივე ბურთულას ერთნაირი მასა აქვს (\(m_{1}=m_{2}\)), პირველი ბურთულა ჩერდება (\(u_{1}=0\)), მეორე მოძრაობს სიჩქარით \(u_{2}=v_{1}\), ე.ი. ბურთულები სიჩქარეებს ცვლიან (და, ე.ი იმპულსებსაც).
თუ შეჯახებამდე მეორე ბურთულას ჰქონდა ნულისაგან განსხვავებული სიჩქარე (\(v_{2}\neq 0\)), ამ ამოცანის დაყვანა ადვილად შეიძლება წინა ამოცანაზე ახალი ათვლის სისტემაზე გადასვლით. რომელიც υ2 სიჩქარით წრფივად და თანაბრად მოძრაობს „უძრავი“ სისტემის მიმართ. ამ სისტემაში მეორე ბურთულა შეჯახებამდე უძრავია, ხოლო პირველი მოძრაობს \(v_{1}^{'}=v_{1}-v_{2}\) სიჩქარით. ზემოთ მოყვანილი ფორმულებით \(u_{1}\) და \(u_{2}\) სიჩქარეების ახალ სისტემაში განსაზღვის შემდეგ, უნდა გადავიდეთ ისევ „უძრავ“ სისტემაზე.
ამგვარად, მექანიკური ენერგიისა და იმპულსის მუდმივობის კანონების გამოყენებით, შეიძლენა განვსაზღვროთ ბურთულების სიჩქარეები შეჯახების შემდეგ, თუ ცნობილია მათი სიჩქარეები შეჯახებამდე.
ცენტრალური შეჯახება პრაქტიკაში ძალიან იშვიათად ხდება, მით უფრო, თუ საქმე ატომებისა და მოლეკულების შეჯახემას შეეხება. არაცენტრალური დრეკადი დაჯახებისას ნაწილაკების (ბირთვების) სიჩქარეები დაჯახებამდე და დაჯახების შემდეგ ერთი წრფის გასწვრივ არაა მიმართული.
არაცენტრალური დრეკადი დაჯახების კერძო შემთხვევას წარმოადგენს ბილიარდის ორი ერთნაირი მასის ბურთულის შეჯახება, როცა შეჯახებამდე ერთი მათგანი უძრავია, ხოლო მეორის სიჩქარე მიმართული არ იყო ბურთულების ცენტრების შემაერთებელი წრფის გასწბრივ (ნახ. 3).

ნახ. 3.

ორი ერთნაირი მასის ბურთულის არაცენტრალური დრეკადი დაჯახება. \(d\)– დამიძნების მანძილი
არაცენტრალური დაჯახების შემდეგ ბურთულები ერთმანეთის მიმართ გარკვეული კუთხით მოძრაობენ. შეჯახების შემდგომი სიჩქარეების \(\vec{u_{1}}\) და \(\vec{u_{2}}\) განსაზღვრისათვის საჭიროა ბურთულების ცენტრების წრფეთა მდებარეობისა და დამიზნების \(d\) მანძილის ცოდნა (ნახ. 3), ე.ი. მანძილი ორ წრფეს შორის, როლებიც ბურთულების ცენტრებზე გადიან და მოძრავი ბურთულის \(\vec{v}_{1}\) სიჩქარის მიმართულების პარალელური არიან. თუ ბურთულების მასები ერთნაერია, მაშინ დრეკადი შეჯახების შემდეგ ბურთულების სიჩქარის ვექტორები \(\vec{u}_{1}\) და \(\vec{u}_{2}\) ყოველთვის ერთმანეთის მართობულადაა მიმართული. ეს ადვილი საჩვენებელია იმპულსისა და ენერგიის მუდმივობის კანონების გამოყენებით. როცა \(m_{1}=m_{2}=m\) ეს კანონები ღებულობენ სახეს:
\(\vec{v_{1}}=\vec{u}_{1}+\vec{u}_{2};\: \vec{v}_{1}^{2}=\vec{u}_{1}^{2}+\vec{u}_{2}^{2}.\)
პირველი ტოლობა ნიშნავს, როს სიჩქარის ვექტორები \(\vec{v}_{1}\), \(\vec{u}_{1}\) და \(\vec{u}_{2}\) ქმნიან სამკუთხედს (იმპულსების დიაგრამა), ხოლო მეორე – რომ, ამ სამკუთხედისათვის სამართლიანია პითაგორას თეორემა, ე.ი. მართკუთხაა. \(\vec{u}_{1}\) და \(\vec{u}_{2}\) კათეტებს შორის კუთხე 90° ტოლია.


