• ჰიდროსტატიკის ელემენტები
• იმპულსის შენახვის კანონი. რეაქტიული მოძრაობა

ვთქვათ $m$ მასის სხეულზე  რაღაც მცირე $\Delta t$ დროის განმავლიბაში მოქმედებს ძალა ​$\vec F$.   ამ ძალის მოქმედებით სხეულის სიჩქარე იცვლება ​$\Delta \vec{v}=\vec{v_{2}}-\vec{v_{1}}$. აქედან გამომდინარე,​$\Delta t​$ დროის განმავლობაში სხეული მოძრაობს აჩქარებით

 ​$\vec{a}=\frac{\Delta \vec{v}}{\Delta t}=\frac{\vec{v_{2}}-\vec{v_{1}}}{\Delta t}​$

დინამიკის ძირითადი კანონიდან (ნიუტონის მეორე კანონი) გამომდინარეობს:

 

 

$\vec{F}=m\vec{a}=m\frac{(\vec{v_{2}}-\vec{v_{1}})}{\Delta t}​$  ან  ​$\vec{F}\Delta t=m\vec{v_{2}}-m\vec{v_{1}}=m\Delta \vec{v}=\Delta (m\vec{v}).​$

 

ფიზიკურ სიდიდეს, რომელიც სხეულის მასისა და მისი სიჩქარის ნამრავლის ტოლია, სხეულის უმპულსი  (ან სხეულის მოძრაობის რაოდენობა) ეწოდება. სხეულის იმპულსი ვექტორული სიდიდეა. იმპულსის ერთეული ​$Si​$ სისტემაშიკოლოგრამ–მეტრია წამში (კმ.მ/წმ).

ახალი ტერმინების გამოყენებით ნიუტონის მეორე კანონი შეიძლება ასე ჩამოვაყალიბით: სხეულის იმპულსის (მოძრაობის რაოდენობის) ცვლილება  ძალის იმპულსის ტოლია. ძალის იმპულსი აღვნიშნოთ ​$\vec{P}​$–თი და მეორე კანონი შეიძლება ასე ჩაიწეროს:

$\vec{F}\Delta t=\Delta \vec{P}.​$

სწორედ ასეთი ზოგადი სახით ჩამოაყალიბა იგი ნიუტონმა. ამ გამოსახულებაში ​$\vec{F}​$ ძალა სხეულზე მოდებული ყველა ძალების ტოლქმედს წარმოადგენს. ეს ვექტორული ტოლობა შეიძლება კოორდინათტა ღერძებზე გეგმილებით ასე ჩაიწეროს:

$F_{x}\Delta t=\Delta P_{x}; F_{y}\Delta t=\Delta P_{y}; F_{z}\Delta t=\Delta P_{z}.​$

ამგვარად, ნებისმიერი ურთიერთმართობულ ღერძზე სხეული იმპულსის გეგმილის ცვლილება იმავე ღერძზე ძალის იმპულსის გეგმილის ტოლია. მაგალითისთვის განვიხილოთ ერთგანზომილებიანი მოძრაობა, ე.ი. სხეულის მოძრაობა ერთ–ერთ საკოორდინატო ღერძზე (მაგ. ​$OY​$–ზე). ვთქვათ სხეული სიმძიმის ძალის მოქმედებით თავისუფლად ვარდება საწყისი ​$v_{0}​$ სიჩქარით; ვარდნის დრო ​$t​$–ა. ​$OY​$ ვერტიკალურად ქვევით მივმართოდ. ​\(t​\) დროის განმავლობაში სიმძიმის ძალის იმპულსი \(mgt​\)–ს ტოლია. ეს იმპულსი სხეულის იმპულსის ცვლილების ტოლია

 

$mgt=\Delta P=m(v-v_{0})​$, სადაც ​$v=v_{0}+gt.​$

 

ეს უბრალო შედეგი ემთხვევა თანაბარაჩქარებული მოძრაობის კინემატიკურ ფორმულას. ამ მაგალითში ძალა ​$t​$ დროის ინტერვალში მოდულით უცვლრლი რჩება. ძალის სიდიდე თუ იცვლება, გამოსახულებაში  ​$t​$ დროის ინტერვალში საშუალო ძალის მნიშვნელობა F_საშ.  უნდა ჩაისვას. ნახ. 1 ნაჩვენებია დროზე დამოკიდებული ძალის იმპულსის განსაზღვრის მეთოდი.

 

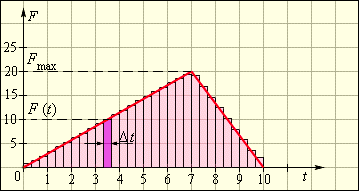
ნახ. 1.

$F(t)​$ დამოკიდებულების გრაფიკიდან ძალის იმპულსის განსაზღვრა.

 

დროის ღერძზე გამოვყოთ Δt მცირე ინტერვალი, რომელშიც ძალა ​$F(t)​$ პრაქტიკულად არ იცვლება. ძალის იმპულსი ​$F(t)\Delta t​$- ​$\Delta t​$ დროის განმავლობაში  დაშტრიხული სვეტის ფართობის ტოლია. თუ დროის მთელ ღერძს 0 –დან  ​$t​$–მდე დავყოფთ ​$\Delta t_{i}​$  მცირე ინტერვალებად, და შემდეგ კი ავჯამავთ ძალის იმპულსებს ყველა ​$\Delta t_{i}​$ მონაკვეტში, მაშინ ჯამური ძალის იმპული   ამ კიბისებური მრუდის მიერ დროის ღერძთან წარმომნილი ფართობის ტოლი გამოვა.  როცა ​$(\Delta t_{i}\rightarrow 0)​$, მოვიღებთ ​$F(t)​$ გრაფიკის მიერ დროის ღერძთან შედგენილ ფართობს.  ​$F(t)​$ გრაფიკის მიხედვით ძალის იმპულსის განსაზღვრის ეს მეთოდი ზოგადია და  ძალის დროში ცვლილების ნებისმიერი კანონისათვის გამოიყენება. მათემატიკური ამოცანა დაიყვანება  ​$F(t)​$–ს  ​$[0;t]​$ ინტერვალში ინტეგრირებაზე.  ნახ. 1–ზე მოცემული ძალის იმპულსი ​$t_{1}=0​$–დან ​$t_{2}=10​$–მდე უდრის:

 

Fსაშ.$(t_{2}-t_{1})=\frac{1}{2}F_{max}(t_{2}-t_{1})=100​$ნ.წმ=100კგ.მ/წმ

Fსაშ ​$=\frac{1}{2}F_{max}=10​$ნ

 

ზოგიერთ შემთხვევაში, საშუალო ძალა  F_საშ შეიძლება განისაზღვროს თუ ცნობილია მისი მოქმედების დრო და სხეულისადმი მინიჭებული იმპულსი. მაგალითად, ფეხბურთელი 0,415 კგ ბურთზე ძლირი დარტყმით, მას ანიჭებს   υ = 30 მ/წმ სიჩქარეს. დარტყმის ხანგრძლივობა დაახლოებით 8·10^–3 წმ–ია.

 დარტყმის შედეგად ბურთის მიერ შეძენილი  ​$P​$  იმპულსი ტოლია:

 

$P=mv=12,5​$კგ.მ/წმ.

 

აქედან გამომდინარე, საშუალო ძალა F_საშ, როლითაც დარტყმის პერიოდში ფეხბურთელი მოქმედებს ბურთზე, ტოლია:

F_საშ ​$=\frac{P}{\Delta T}=1,56\cdot 10^{3}​$ნ

 

ეს ძალიან დიდი ძალაა. ის დაახლოებით 160 კგ მასის წონის ტოლია.

თუ სხეული  ძალის მოქმედების პერიოდში რაღაც მრუდწირულ ტრაექტორიაზე მოძრაობს, მაშინ სხეულის საწყისი ​$\vec{P_{1}}​$ და საბოლოო ​$\vec{P_{2}}​$ იმპულსები შეიძლება განსხვავდებოდეს როგორც მოდულით, ასევე მიმართულებითაც. ამ შემთხვევაში იმპულსის ცვლილების ​$\Delta \vec{P}​$ განსაზღვრისათვის ხელსაყრელია იმპულსების დიაგრამას გამოყენება, რომელზეც გამოსახულია პარალელოგრამის წესით აგებული  ​$\vec{P_{1}}​$ და ​$\vec{P_{2}}​$ ვექტორები და ასევე ვექტორი ​$\Delta \vec{P}=\vec{P_{2}}-\vec{P_{1}}​$.  ნახ. 2–ზე  გამოსახულია იმპულსების დიაგრამა  უსწორმასწორო კედლიდან არეკვლილი ბურთისათვის. ​$m​$ მასის ბირთი დაეჯახა კედელს ​$\vec{v_{1}}​$ სიჩქარით ნორმალისადმი (ღერძი ​$OX​$)  ​$\alpha​$  კუთხით, გადაიხარა ნორმალიდან  ​$\beta​$ კუთხით და გააგრძელა გზა ​$\vec{v_{2}}​$ სიჩქარით. ბურთის კედელთან კონტაქტის დროს მასზე მოქმედებდა რაღაც ​$\vec{F}​$ ძალა, რომლის მიმართულება ემთხვევა ​$\Delta \vec{P}​$ ვექტორს.

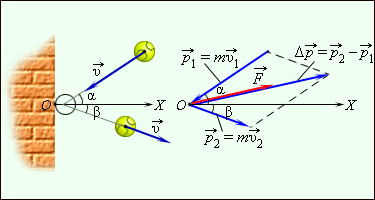
ნახ. 2.

უსწორმასწორო კედლიდან ბურთის არეკვლა და იმპულსების დიაგრამა

 

დრეკად კედელზე ​$m​$ მასის ბურთს ნორმალური (პირდაპირი) ​$\vec{v_{1}}=\vec{v}​$ სიჩქარით შეჯახებისას, არეკვლის შემდეგ აქვს ​$\vec{v_{2}}=-\vec{v}​$ სიჩქარე. აქედან გამომდინარეობს, რომ არეკვლისას იმპულსის ცვლილება ტოლია ​$\Delta \vec{P}=-2m\vec{v}.​$  ​$OX​$  ღერძზე დაგეგმილების შედეგი შეიძლება ჩაიწეროს სკალარული ფორმით Δp_x = –2mυ_x.  OX ღერძი მიმართულია კედლისაკენ, ამიტომ ​$v_{x}<0​$ და ​$\Delta p_{x}>0​$. აქედან გამომდინარე, იმპულსის ცვლილების მოდული ​$\Delta P​$ $v​$ $v$ ბურთის სიჩქარიეს υ მოდულთან დაკავშირებულია ტოლობით ​$\Delta P=2mv​$.