| პოტენციური ენერგია | |
|
პოტენციური ენერგია - სხეულების ან სხეულის ნაწილების ურთიერთქმედების ენერგია. პოტენციური ენერგია (ლათ. potentia - შესაძლებლობა) განისაზღვრება სხეულების ან სხეულის ნაწილების ურთიერთგანლაგებით ანუ მათ შორის მანძილებით. |
|
|
დედამიწიდან აწეული სხეულის პოტენციური ენერგია. სიმძიმის ძალის მუშაობა |
|
|
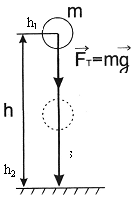
ვთქვათ სხეული თავისუფლად ვარდება დედამიწის ზედაპირიდან h1 დონიდან h2 დონეზე. მაშინ:\(A=Fscos\alpha =mg\left ( h_{1}-h_{2} \right )=mgh_{1}-mgh_{2}=\left ( mgh_{2}-mgh_{1} \right )\) ვარდნისას სიმძიმის ძალა ასრულებს დადებით მუშაობას, სხეულის ზემოთ მოძრაობისას - უარყოფითს. სიდიდეს Eდ = mgh სხეულისა და დედამიწის ურთიერთქმედების პოტენციურ ენერგიას უწოდებენ. |
|
|
ასე რომ A = - (Ep2 - Ep1) = -ΔEp სიმძიმის ძალის მუშაობა ტოლია პოტენციალური ენერგიის ცვლილებისა შებრუნებული ნიშნით. ანუ, თუ პოტენციური ენერგია იზრდება (სხეული ზევით ადის), მაშინ სიმძიმის ძალა ასრულებს უარყოფით მუშაობას და პირიქით. |
Eз = mgh
A = - (Ep2 - Ep1) = -ΔEp |
|
რადგან პოტენციური ენერგია განისაზღვრება კოორდინატით, ამიტომ პოტენციური ენერგიის სიდიდე განისაზღვრება კოორდინატთა სისტემის შერჩევით (ნულოვანი დონის შერჩევით). ანუ, ის განისაზღვრება მუდმივი სიდიდის სიზუსტით. მოცემულ ამოცანაში მოხერხებულია ათვლის წერტილად ავიღოთ დედამიწის ზედაპირის დონე. |
|
|
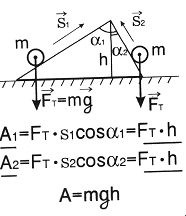
თუ სხეული სიმძიმის ძალისადმი კუთხით მოძრაობს, მაშინ, როგორც ჩანს ნახაზიდან, სიმძიმის ძალის მუშაობა დამოუკიდებლად ტრაექტორიისა განისაზღვრება სხეულის მდებარეობის ცვლილებით (ნახაიდან მხოლოდ h-ის ცვილებით). თუ სხეული მოძრაობს ნებისმიერი ტრაექტორიით, მისი წარმოდგენა შეიძლება ჰორიზონტული უბნების ჯამის სახით, რომელზეც სიმძიმის ძალის მუშაობა ნულის ტოლია და ვერტიკალური უბნების ჯამის სახით, რომელზეც ჯამური მუშაობა იქნება А=mgh. სიმძიმის ძალის მუშაობა არ არის დამოკიდებული ტრაექტორიის ფორმაზე და განისაზღვრება მხოლოდ სხეულის საწყისი და საბოლოო მდებარეობებით. ჩაკეტილ ტრაექტორიაზე სიმძიმის ძალის მუშაობა ნულის ტოლია, რადგან პოტენციური ენერგია არ იცვლება. |
|
|
გრავიტაციული ძალებით ურთიერთმოქმედი სხეულების პოტენციური ენერგია. გრავიტაციული ძალის მუშაობა. |
|
|
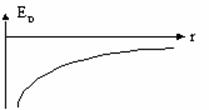
ნიშანი "-" მიუთითებს იმას, რომ ეს არის მიმზიდველი სხეულების ებერგია. სხეულების მიახლოებისას პოტენციური ენერგიის მოდული იზრდება. ორი ასტრონომიული ობიექტის ურთიერთმიახლოებისთვის შესრულებული მუშაობა: |
|
|
დრეკადად დეფორმირებული სხეულის პოტენციური ენერგია. დრეკადობის ძალის მუშაობა. |
|
|
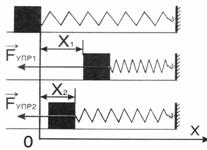
ფორმულის გამოსაყვანად გამოვიყენოთ, რომ მუშაობა რიცხობრივად ტოლია ძალის კოორდინატზე დამოკიდებულების გრაფიკის ქვეშა ფართობისა. მცირე დრეკადი დეფორმაციებისას დრეკადობის ძალა პირდაპირპროპორციულია აბსოლუტური დეფორმაციისა (ჰუკის კანონი) იხ. ნახაზი. მაშინ დეფორმაციის работа х1-დან х2-მდე ცვლილებისას მუსაობა ტოლია:
|
|
|
ჰუკის კანონის გათვალისწინებით მივიღებთ: |
|
|
ასე რომ, თუ დრეკადად დეფორმირებული სხეულის პოტენციურ ენერგიად მივიღებთ სიდიდეს
სადაც k - სიხისტის კოეფიციენტია, ხოლო х - სხეულის აბსოლუტური დეფორმაციაა, მაშინ შეგვიძლია დავასკვნათ, რომ ანუ ძალის მუშაობა სხეულის დეფორმაციისას ტოლია ამ სხეულის პოტენციური ენერგიის ცვლილებისა შებრუნებული ნიშნით. |
|
|
დრეკადობის ძალის მუშაობა დამოკიდებულია მხოლოდ სხეულის (დეფორმაციის საწყის და საბოლოო) კოორდინატებზე და შესაბამისად, არ არის დამოკიდებული ტრაექტორიაზე. ჩაკეტილ ტრაექტორიაზე მუშაობა ნულია. |
|
|
კონსერვატული ძალები. კონსერვატული (შენარჩუნებადი) ეწოდება ძალებს, რომელთა მუშაობაც არ არის დამოკიდებული ტრაეტორიაზე და ჩაკეტილ ტრაექტორიაზე ნულია (ეს ძალები არ არის სიჩქარეზე დამოკიდებული). მაგალითები: გრავიტაციული, დრეკადი. |
|
|
დისიპაციური ძალები დისიპაციური (გაბნევითი) ეწოდება ძალებს, რომელთა მუშაობაც დამოკიდებულია ტრაექტორიაზე და ჩაკეტილ ტრაექტორიაზე არ არის ნულის ტოლი (ასეთი ძალები დამოკიდებულია სიჩქარეზე). მაგალითი: ხახუნის ძალა. |
|

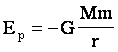 , სადაც r- ურთიერთმოქმედ სხეულებს შორის მანძილია.
, სადაც r- ურთიერთმოქმედ სხეულებს შორის მანძილია. .
.
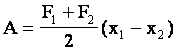 .
.
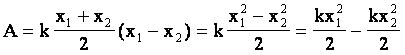

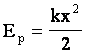 ,
,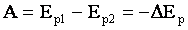 ,
,