| მრუდწირული მოძრაობა | |
| მრუდწირული მოძრაობისას სიჩქარი ვექტორი ყოველთვის მოძრაობის ტრაექტორიის მხების გასწვრივ არის მიმართული. ნებისმიერი მრუდწირული მოძრაობის წარმოდგენა შეიძლება წრფივი მოძრაობებისა და სხვადასხვა რადიუსიან წრეწირებზე მოძრაობების ჯამის სახით.სიჩქარე იცვლება როგორც სიდიდით, ასევე მიმართულებითაც. აჩქარების ვექტორი კუთხეს ადგენს სიჩქარის ვექტორთან. | 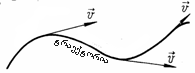 |
| წერტილის თანაბარი მოძრაობა წრეწირზე | |
|
წერტილის თანაბარი მოძრაობა წრეწირზე არის წერტილის მუდმივი მოდულის მქონე (v=const) სიჩქარით მოძრაობა წრიულ ტრაექრტორიაზე. მაგრამ რადგან სიჩქარე ყოველთვის მიმართულია მოძრაობის ტრაექტორიის მხების გასწვრივ, ამიტომ მიმართულებით ის იცვლება. ანუ წრეწირზე თანაბარი მოძრაობა არის აჩქარებული მოძრაობა! წერტილი ასრულებს გადაადგილებას მოდულით მუდმივი სიჩქარით, შედეგად: ამ შემთხვევაში წერტილის სიჩქარეს ეწოდება წირითი სიჩქარე (ℓ–რკალის სიგრძეა). წირითი სიჩქარის ვექტორი მოცემულ წერტილში წრეწირის მხების გასწვრივ არის მიმართული. |
 |
|
სხეულის მდებარეობის დახასიათება შეიძლება კუთხური გადაადგილებით (შემობრუნების კუთხით) φ. ავიღოთ რამდენიმე კონცენტრული წრეწირი და ავაგოთ ყველასთვის ცენტრალური φ კუთხე ისე, რომ ამ წრეწირების რადიუსები, რომლებიც კუთხეს ადგენენ, ერთმანეთს დაემთხვნენ. ნახატიდან ჩანს, რომ ერთდაიგივე φ კუთხეს შეესაბამება ერთი წრეწირისთვის რკალი ℓ და რადიუსი r, ხოლო მეორესთვის – რკალი L და რ ადიუსი R. კუთხის ზომად შეიძლება მივიღოთ რკალის სიგრძის ფარდობა რადიუსთან: ამ შემთხვევაში კუთხის ზომის ერთეულს უწოდებენ ე.წ. რადიანს (მოკლედ –რად). |
|
|
ცენტრალური კუთხე ტოლია ერთი რადიანის, თუ რკალის სიგრძე წრეწირის რადიუსის ტოლია. თუ სხეულმა შეასრულა სრული ბრუნი, მაშინ რკალის სიგრძე ტოლია წრეწირის სიგრძის. შესაბამისად: |
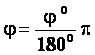 |
|
წერტილის თანაბარი მოძრაობა წრეწირზე ეს არის მოძრაობა, როცა წერტილი დროის ნებისმიერ ტოლ შუალედებში ასრულებს ერთნაირ კუთხურ გადაადგილებებს (შემობრუნდება თანატოლი კუთხეებით). თუ მოძრაობას შემობრუნების კუთხით დავახასიათებთ, მაშინ მოსახერხებელია კუთხური სიჩქარი შემოღება: |
 |
შეიძლება ითქვას, რომ წრეწირზე თანაბარი მოძრაობა ეწოდება მუდმივი კუთხური სიჩქარით მოძრაობას. წირითი და კუთხური სიჩქარეები უკავშირდებიან ერთმანეთს ასე: 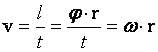 , ანუ. , ანუ. 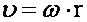 . . |
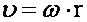 |
|
ბრუნვითი მოძრაობის მნიშვნელოვანი მახასიათებლები არის სიხშირე და პერიოდი. პერიოდი არის ფიზიკური სიდიდე, რომელი აჩვენებს, თუ რისი ტოლია დრო, რომელშიც წერტილი ერთ სრულ ბრუნს ასრულებს. თუ N-ით აღვნიშნავთ t დროში შესრულებულ ბრუნვათა რიცხვს, ხოლო Т – თი პერიოდს, მაშინ: სი სისტემაშმობრუნდება 2π კუთხით, ამიტომ სიხშირე – არის ბრუნვათა რიცხვი, რაც წერტილმა დროის ერთეულში შეასრულა:
სი სისტემაში ზომის ერთეულია – ჰც (ჰერცი). სიხშირე ტოლია ერთი ჰერცის, თუ 1 წამის განმავლობაში წერტილი ასრულებს ერთ ბრუნს (1ჰც=1წმ-1). სიხშირე და პერიოდი – ურთიერთშებრუნებული სიდიდეებია: |
|

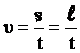 .
.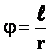 .
.
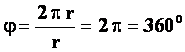 - წერტილის სრული ბრუნი შეადგენს
- წერტილის სრული ბრუნი შეადგენს 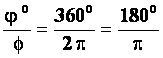 . შესაბამისად:
. შესაბამისად:  .
. .
. .
. . შესაბამისად:
. შესაბამისად:  .
.