| თანაბრადცვლადი მოძრაობა. აჩქარება | |
|
მოძრაობას, რომლის დროსაც სხეულის სჩქარე იცვლება ერთნაირად დროის ტოლი შუალედების განმავლობაში, თანაბრადცვლადი მოძრაობა ეწოდება. |
|
|
ავღნიშნოთ: \(\dpi{120} \vec{v}_{0}\) - საწყისი სიჩქარი ვექტორი, \(\dpi{120} \Delta \vec{v}=\vec{v}-\vec{v}_{0}\) - სიჩქარის ცვლილება, ხოლო Δt - დროის შუალედია. ვთქვათ Δt1= Δt2=Δt3=..., მაშინ განსაზღვრის თანახმად \(\dpi{120} \Delta \vec{v}_{1}=\Delta \vec{v}_{2}=\Delta \vec{v}_{3}=...\) |
|
|
შეასბამისად, \(\dpi{120} \frac{\Delta \vec{v}_{1}}{\Delta t_{1}}=\frac{\Delta \vec{v}_{2}}{\Delta t_{2}}=\frac{\Delta \vec{v}_{3}}{\Delta t_{3}}=...=const\)
ასე რომ ეს მოძრაობის მახასიათებელია. |
|
|
თუ t0=0, მაშინ \(\dpi{120} \vec{a}=\frac{\vec{v}-\vec{v}_{0}}{t}\) |
\(\dpi{120} \vec{a}=\frac{\vec{v}-\vec{v}_{0}}{t}\) |
|
აჩქარება - ფიზიკური სიდიდეა, რომელიც სიჩქარის ცვლილების სისწრაფეს ახასიათებს და (თანაბრადცვლადი მოძრაობისას) რიცხობრივად ტოლია სიჩქარის ცვლილების ვექტორის ფარდობისა იმ დროის ინტერვალთან, რომელშიც მოხდა ეს ცვლილება. |
|
|
აჩქარება თანაბრადცვლადი მოძრაობისას აჩვენებს, რამდენად იცვლება მოძრაობის მყისიერი სიჩქარე დროის ერთეულში. სი სისტემაში აჩქარების ერთეულია მ/წმ2. |
მაგალითად, აჩქარება უდრის 5 მ/წმ2 - ეს ნიშნავს, რომ, მოძრაობს რა თანაბრადაჩქარებულად, სხეული იცვლის სიჩქარეს 5მ/წმ-ით თავისი მოძრაობის ყოველ წამში. |
|
არათანაბრადცვლადი მოძრაობის შემთხვევაში: \(\dpi{120} \vec{a}\)საშ\(\dpi{120} =\frac{\Delta \vec{v}}{\Delta t}\); მაშინ მყისიერი აჩქარება \(\dpi{120} \vec{a}=\lim_{\Delta t\rightarrow 0}\frac{\Delta v}{\Delta t}=\vec{v}{}{\color{White} '}{}'\) |
|
|
თანაბრადცვლად მოძრაობას ეწოდება თანაბარაჩქარებული, თუ სიჩქარის მოდული იზრდება. |
თ.ა.მ. პირობა -\(\dpi{150} \LARGE \vec{v}_{0}\uparrow \uparrow \vec{a}\). |
|
თანაბრადცვლად მოძრაობას ეწოდება თანაბარშენელებული, თუ სიჩქარის მოდული მცირდება. |
თ.შ.მ. პირობა - \(\dpi{120} \LARGE \vec{v}_{0}\uparrow \downarrow \vec{a}\). |
|
თანაბრადცვლადი მოძრაობის გრაფიკები. |
|
| \(\dpi{150} \vec{v}=\vec{v}_{0}+\vec{a}t\) | \(\dpi{150} \vec{v}=\vec{v}_{0}+\vec{a}t\) |
|
ან \(\dpi{150} v_{x}=v_{0x}+a_{x}t\) - პროექციებში; ან\(\dpi{150} v}=v_{0}+at\) – მოდულით. |
\(\dpi{150} v_{x}=v_{0x}+a_{x}t\) |
|
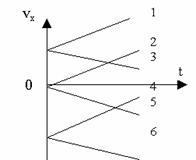
წრფივი ფუნქცია. გრაფიკი - წრფივია. |
|
|
მოძრაობები, რომელთა მიმართულება ემთხვევა კოორდინატთა ღერძის მიმართულებას:
|
 |
|
გადაადგილება თანაბრადცვლადი მოძრაობისას. |
|
|
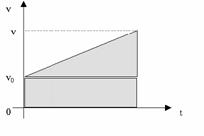
სიჩქარის გრაფიკის ქვეშა ფართობი რიცხობრივად გადაადგილების ტოლია, შესაბამისად, ტრაპეციის ფართობი რიცხობრივად უდრის გადაადგილებას. |
 |
 |
თ.ა.მ.-თვის მექანიკის ძირითადი ამოცანის ამოხსნა: \(\dpi{150} s=v_{0}t+\frac{at^{2}}{2}\) \(\dpi{150} x=x_{0}+v_{0}t+\frac{at^{2}}{2}\) |
|
გადაადგილებისა და კოორდინატის გრაფიკი. |
|
|
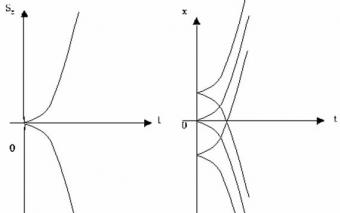
ფუნქციები \(\dpi{150} x=x_{0}+v_{0}t+\frac{at^{2}}{2}\) და \(\dpi{150} s=v_{0}t+\frac{at^{2}}{2}\)- კვადრატულებია. გრაფიკი – პარაბოლაა! |
|
 |
|
