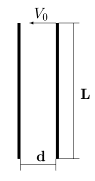
მცირე ზომის ბურთი, რომელსაც ვერტიკალური მიმართულებით  სიჩქარე გააჩნია, იწყებს მოძრაობას ორ პარალელურ კედელს შორის სივრცეში.

რამდენჯერ მოხვდება ბურთი კედელს მიწაზე დავარდნამდე? კედლებს შორის მანზილია , მათი სიმაღლეა . . ბურთის კედელთან დაჯახება ჩათვალეთ აბსოლიტურად დრეკადად.

$Ox$ ღერძი მივმართოთ ჰორიზონთალურად, მარცხნივ, $Oy$ ვერტიკალურად ქვევით. $Ox$ღერძის მიმართ მოძრაობა დაჯახებიდან დაჯახებამდე თანაბარია, რადგან ამ ღერძის მიმართ, ბურთზე მოქმედი სიმძიმის ძალის გეგმილი 0-ის ტოლია. ბურთის სიჩქარის გეგმილი- $v_{x}=v_{0}$ დაჯახების შემდეგ იცვლის მხოლოდ მიმართულებას, მოდული არ იცვლება, რადგან დაჯახება აბსოლიტურად დრეკადია. დრო ორ მომდევნო დაჯახებას შორის ტოლია $t=\frac{d}{v_{0}}$.

$O_{y}$ ღერძის მიმართ მოძრაობა იწყება უსაწყისო სიჩქარით $a_{y}=g$ აჩქარებით. $t$ დროში სხეული ვერტიკალურად დაეშვება $h=\frac{gt^{2}}{2}$  მანძილზე. სანამ იგი გვერტიკალურად გაივლის $L$ მანძილს, ის მოასწრებს დაეჯახოს იმდენჯერ, რამდენჯერაც $h$ მოთავსდება $L$-ში, ანუ: $n=\frac{L}{h}=\frac{2Lv_{0}^{2}}{gd^{2}}(*)$