თუ 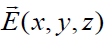   ფუნქციით მოცემული გვაქვს ძალური ველი, ნებისმიერ ორ წერტილს შორის პოტენციალთა სხვაობა, როგორც ვიცით, არის:

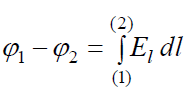               (9.6)

გვაინტერესებს პირიქით, თუ ვიცით ფუნქცია φ (x, y, z) , მოვძებნოთ 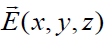 დაძაბულობა.

განვსაზღვროთ ველის ძალების მიერ q_tst საცდელი მუხტის მცირე 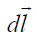 გადადგილებაზე შესრულებული მუშაობა ორი მეთოდით:

1. dA = q_tst·E_l ·dl.

აქ გამოყენებულია ჩვენთვის გარგად ცნობილი თანაფარდობები:

dA = Fl •dl – ელემენტური მუშაობის განსაზღვრა;

F_l = q_tst·E_l – დაძაბულობის განსაზღვრა;

2. dA = – q_tst·dφ.

აქ დავეყრდენით პოტენციალთა სხვაობის განსაზღვრას q_tst·(φ₁ -φ₂) = A₁₂. ნიშანი “–“, აიხსნება იმით, რომ dφ - ეს არის პოტენციალის უსასრულოდ მცირე ნაზრდი Δφ = (φ₂ - φ₁) = –(φ₁ - φ₂).

ამოვწეროთ 1 და 2 თანაფარდობები განტოლებათა სისტემის სახით:

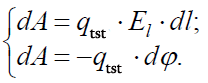
აქედან მივიღებთ:

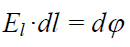   ან: 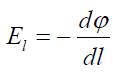               (17.12)

ეს თანაფარდობაა ნიშნავს, რომ ველის დაძაბულობის გეგმილი 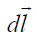   მიმართულებაზე ველის ამ წერტილიდან წერტილამდე ველის პოტენციალის ცვლილების სიჩქარის ტოლია. ნიშანი “–“ ასახავს იმ ფაქტს, რომ ველის დაძაბულობა მიმართულია პოტენციალის კლების მიმართულებით.

რადგან 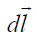 უსასრულოდ მცირე გადაადგილების მიმართულება ნებისმიერად გვქონდა აღებული, ამიტომ ის შეიძლება იყოს მიმართული ნებისმიერი კოორდინატთა ღერძის გასწვრივ და ამიტომ მივიღებთ:

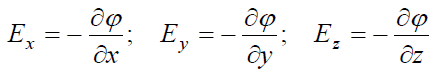.            (17.13)

ამიტომ თვით ელექტრული ველის დაძაბულობის ვექტორისთვის შეგვიძლია დავწეროთ:

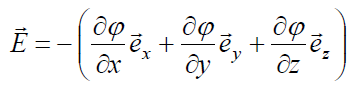.                       (17.14)

ანუ მათემატიკურად ეს შეიძლება ჩაიწეროს გრადიენტის ოპერატორის მეშვეობითაც:

                       (17.15)

ნიშანი «მინუსი» გრადიენტის წინ მიუთითებს, რომ  ელექტროსტატიკური ველის დაძაბულობის ვექტორი ყოველთვის მიმართულია მისი პოტენციალის კლების მიმართულებით.

მოვიყვანოთ მიღებული შედეგის გამოყენების მაგალითი.

მაგალითი. განვსაზღვროთ  R  რადიუსის მქონე თანაბრად დამუხტული რგოლის ელექტრული ველის დაძაბულობა რგოლის ღერძზე ველის φ(x) პოტენციალის ცნობილი დამოკიდებულებით. რგოლის მუხტია q, x – არის რგოლის ცენტრიდან დაშორება ღერძზე.

წინა თავში მივიღეთ, რომ  (იხ. 17.11)

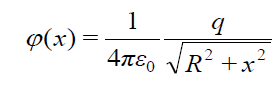
(17.15)-ის გამოყენებით მივირებთ:

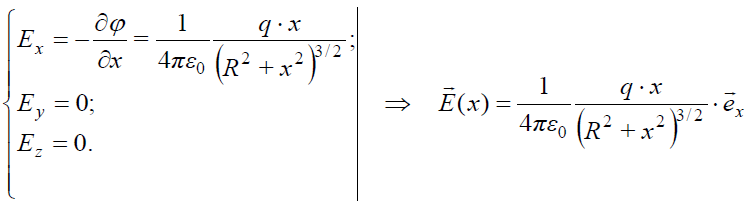
შედეგი, რა თქმა უნდა, ზუსტად ემთხვევა ადრე მიღებულ გამოსახულებას (15.6).