მარტივად საჩვენებელია, რომ qi მუხტების სისტემის ველის პოტენციალისთვის სამართლიანია სუპერპოზიციის პრინციპი: ის ცალკეული მუხტის მიერ მოცემულ წერტილში შექმნილი პოტენციალის ალგებრული ჯამის ტოლია:
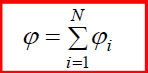 (17.9)
(17.9)
ამ დებულების დამტკიცება ემყარება ორ ჩვენთვის ცნობილ გარემოებას: 1) პოტენციალი საცდელი მუხტის მოცემული წერტილიდან ნორმირების წერტილში გადატანაზე შესასრულებელი კუთრი მუშაობის ტოლია; 2) ძალის მუშაობა არის ადიტიური სიდიდე, ანუ სხეულზე მოქმედი რამდენიმე ძალის მუშაობა ყოველთვის ტოლია ცალკეული ძალის ამ სხეულზე მოქმედებით შესრულებული მუშაობების ალგებრული ჯამისა.
წერტილოვანი მუხტების სისტემის ველისთვის, შესაბამისად, შეიძლება
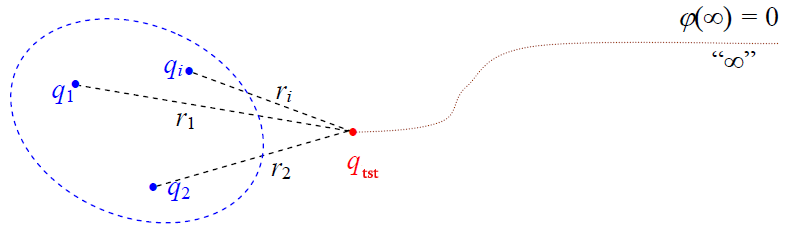
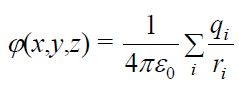 (17.10)
(17.10)
სადაც ri – არის i-ური მუხტისგან დაშორება {x,y,z}კოორდინატების მქონე ველის წერტილამდე. მოვიყვანოთ განვრცობილი დამუხტული სხეულის მიერ შექმნილი ველის პოტენციალის გამოთვლის მარტივი მაგალითი, რომელიც ემყარება პოტენციალთა სუპერპოზიციის პრინციპს.
მაგალითი. განვსაზღვროთ თანაბრად დამუხტული R რადიუსის მქონე რგოლის მიერ შექმნილი ველის φ(x) პოტენციალი ამ რგოლის ღერძზე. რგოლის მუხტია q, x – არის რგოლის ცენტრიდან დაშორება.
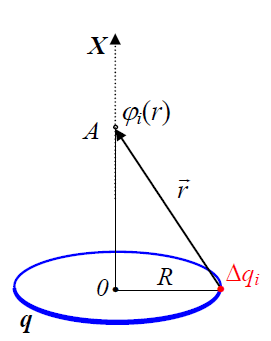
პოტენციალი არის სკალარული სიდიდე და რგოლის აზრობრივად Δqi მუხტის მქონე ელემენტებად დაყოფის შემდეგ, სუპერპოზიციის პრინციპის შესაბამისად უნდა შევკრიბოთ სრულიად ერთნაირი სიდიდეები - ველის პოტენციალები, რომლებსაც ჩვენთვის საინტერესო წერტილში ქმნიან რგოლის ცალკეული ელემენტები:
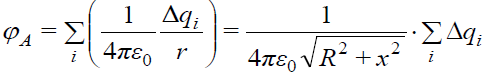
დარჩენილი ჯამი გვაძლევს, რა თქმა უნდა, რგოლის სრულ q მუხტს. ამიტომ შედეგი საბოლოოდ ასე ჩავწეროთ:
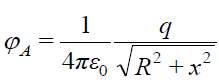 (17.11)
(17.11)
ეს შედეგი მათემატიკური თვალსაზრისით ძალიან მარტივად მივიღეთ სწორედ პოტენციალის სკალარული ხასიათის გამო.


