ელექტრული ველის დაძაბულობა არის ვექტორული სიდიდე. გარკვეულ შემთხვევებში უფრო მოხერხებულია ველის სკალარული მახასიათებლების - პოტენციალთა სხვაობისა და პოტენციალის გამოყენება. მათი განსაზღვრებისთვის დავეყრდნობით მუხტზე ელექტრულ ველში მოქმედი ძალის კონსერვატულობის თვისებას. კონსერვატულობის თვისება გამომდინარეობს კულონის ძალის ცენტრულობიდან. კლასიკური მექანიკის განმარტებით ცენტრული ეწოდება ძალას, რომლის სიდიდეც დამოკიდებულია მხოლოდ ურთიერთქმედ სხეულებს შორის მანძილზე და მიმართულია მათ ცენტრებს შორის შემაერთებელი წირის გასწვრივ. გავიხსენოთ ასევე, რომ კონსერვატული ეწოდება ძალებს, რომელთა შესრულებული მუშაობა არ არის დამოკიდებული მოძრაობის ტრაექტორიის ფორმაზე. ასეთი ძალების მიერ შესრულებული მუშაობა განისაზღვრება მხოლოდ სხეულის გადაადგილების საწყისი და საბოლოო კოორდინატებით.
ელექტრული ველების სუპერპოზიციის პრინციპიდან გამომდინარეობს, რომ საცდელი მუხტის გადაადგილებაზე შესრულებული მუშაობა უძრავი მუხტების მიერ შექმნილ ველში, არის ალგებრული ჯამი მუშაობებისა, რომელსაც ასრულებენ თითოეული შემადგენელი მუხტის მხრიდან საცდელ მუხტზე მოქმედი ძალები. ანუ ასეთი ძალების („კულონური ძალების“) ველი ასევე არის კონსერვატული.
ამდენად, წერტილოვანი მუხტის წერტილი 1-დან წერტილ 2-ში გადაადგილებაზე ველის მიერ შესრულებული მუშაობა A1-2 არის ამ ველის მახასიათებელი. მაგრამ ის დამოკიდებულია საცდელი მუხტის სიდიდეზეც. იმისათვის რათა დავახასიათოთ მხოლოდ ველი, უნდა გავყოთ ეს მუშაობა საცდელი მუხტის სიდიდეზე. რასაც მივიღებთ არის სწორედ „პოტენციალთა სხვაობა“.
(განსაზღვრება) 1 და 2 წერტილებს შორის ელექტროსტატიკური ველის პოტენციალთა სხვაობა ეწოდება ველის მიერ ამ წერტილებს შორის საცდელი მუხტის გადაადგილებაზე შესრულებული მუშაობის ფარდობას ამ საცდელი მუხტის სიდიდესთან.
\(\varphi _{1}-\varphi _{2}=\frac{A_{12}^{filed}}{q_{tst}}\) (17.1)
Si სისტემაში პოტენციალთა სხვაობის ერთეული არის ვოლტი (1ვოლტი=1ჯოული/კულონი). თუ ვისწავლით რამენაირად (თეორიულად ან ექსპერიმენტულად) უძრავი მუხტების სისტემის ველის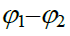 
პოტენციალთა სხვაობის განსაზღვრას, ეს მოგვცემს საშუალებას ნებისმიერი წერტილოვანი q მუხტის ამ ველში გადაადგილებაზე ველის მიერ შესრულებული მუშაობა ვიპოვოთ ფორმულით:
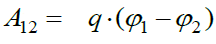(17.2)
ამდენად, პოტენციალთა სხვაობა არის ელექტრული ველის ენერგეტიკული მახასიათებელი, რადგან უშუალო კავშირშია მუშაობის ცნებასთან.
მექანიკაში გვახსოვს პოტენციური ენერგიის ცნება და მუშაობის განმარტება, პრინციპით: ველის ძალების მუშაობა პოტენციური ენერგიის დანაკლისის ტოლია. ჩავწეროთ ფორმალურად ეს პრინციპი:
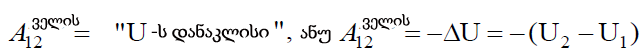17.3)
აქ U1 და U2 – პოტენციური ენერგიებია სისტემის «საწყის» («1») და «საბოლოო» («2») მდგომარეობებში, შესაბამისად. ჩვენი უძრავი მუხტების ელექტრული ველის შემთხვევაში - ეს არის წერტილოვანი q მუხტის ენერგია «1» (კოორდინატებით {x1,y1,z1})) მდგომარეობაში და მისი ენერგია «2» (კოორდინატებით{x2,y2,z2}) მდგომარეობაში. ანუ ამ ველში მუხტის პოტენციური ენერგია არის კოორდინატების სკალარული ფუნქცია U = U(x,y,z) (ან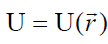 
). გამოსახულებების (17.2) და (17.3) შედარებით ვხედავთ, რომ მოხერხებულია ჩაითვალოს, რომ პოტენციალთა სხვაობა არის სხვაობა ველის წერტილთა კოორდინატების კიდევ ერთი სკალარული \(\varphi\left ( x,y,z \right )\)ფუნქციის . ის დაკავშირებულია U(x,y,z) პოტენციური ენერგიის ფუნქციასთან ამ მარტივი ტოლობით
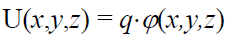ანუ რადგან
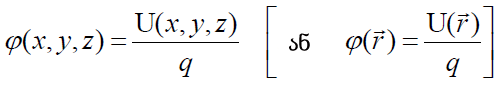(17.4)
ამბობენ, რომ ის „რიცხობრივად ერთეულოვანი დადებითი მუხტის პოტენციური ენერგიის ტოლია“ ველის მოცემულ წერტილში. ამ ფუნქციას ეწოდება ელექტროსტატიკური ველის „პოტენციალი“ მოცემულ წერტილში.
მთავარი არის, თუ როგორ ვიპოვოთ ეს ფუნქცია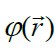 
(და ე.ი. 
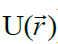) მუხტების კონკრეტული სისტემის ველისთვის, როგორი უნდა იყოს მოქმედებათა თანმიმდევრობა. უწინარეს ყოვლისა უნდა შევთანხმდეთ ნორმირების პირობებზე: უნდა აირჩეს წერტილი Р0, რომელშიც ველის პოტენციალს ჩავთვლით ნულად 
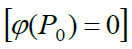. ბევრ შემთხვევაში ასეთ წერტილს არჩევენ უსასრულოდ დაშორებულს, სადაც ველი არ არის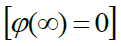 
ამისათვის უნდა მოიძებნოს ველის „კუთრი“ მუშაობა - ანუ მუშაობა, შეფარდებული მოცემული Р(x,y,z) წერტილიდან Р0 ნორმირების წერტილში გადასატანი საცდელი მუხტის სიდიდესთან. ანალიზური სახით ეს პოტენციალის განსაზღვრება ასე შეიძლება ჩაიწეროს:
(განსაზღვრება)
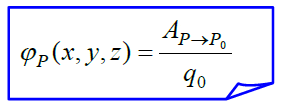(17.5)
გამოვსახოთ პოტენციალთა სხვაობა და პოტენციალი ველის ძალური მახასიათებლებით. ამისთვის ვწერთ:
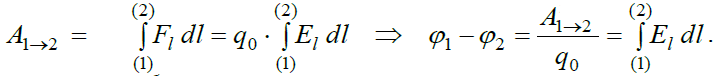
ამოვწეროთ უკანასკნელი ტოლობა:
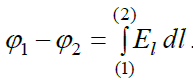(17.6)
ეს გვაძლევს პოტენციალთა სხვაობის მოძებნის საშუალებას დაძაბულობის ცნობილი ფუნქციის მეშვეობით. ანალოგიურად პოტენციალისთვის:
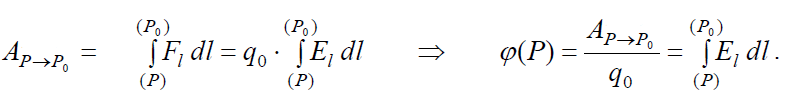
და საბოლოოდ ნებისმიერი (x,y,z) კოორდინატების მქონე Р წერტილის პოტენციალისთვის გვექნება:
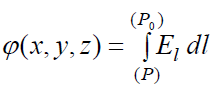(17.7)