16.3. განფენილი დამუხტული სხეულების ელექტრული ველის დაძაბულობის გათვლის მაგალითები გაუსის თეორემის გამოყენებით

ადრე აღვნიშნეთ, მუხტის მოცემული განაწილების მიხედვით მისი ელექტრული ველის დაძაბულობის გათვლა სივრცეში შესაძლებელია სუპერპოზიციის პრინციპის გამოყენებით („პირველი მეთოდი“ – „უშუალოდ“) პრინციპულად ყოველთვის. მაგრამ გარდა ძალიან მარტივი შემთხვევებისა ასეთ გათვლებს ძალიან რთულ მათემატიკურ პროცედურებამდე მივყავართ. გაუსის თეორემა საშუალებას იძლევა მნიშვნელოვნად გავამარტივოთ ტექნიკური პრობლემები, ოღონდ თუ ადგილი აქვს გარკვეულ სიმეტრიას მუხტის სივრცულ განაწილებაში. ბრტყელი, ღერძული ან სფერული სიმეტრიის არსებობა არის პრინციპული მომენტი, ის საშუალებას იძლევა „აპრიორი“ გავაკეთოთ დასკვნა ველის სტრუქტურაზე, რის შემდეგაც შეიძლება შეირჩეს \dpi{120} \Sigma\(. ზედაპირი ისე, რომ მაქსიმალურად გამარტივდეს ზედაპირული ინტეგრალის გამოთვლა გაუსის ფორმულირებაში. ამ ზედაპირის ნაწილები უნდა იყოს დაძაბულობის ვექტორისადმი ან მართობული (\)\dpi{120} \cos \alpha =1\(), ან პარალელური (\)\dpi{120} \cos \alpha =0\(). დაძაბულობის ვექტორის მოდული უნდა იყოს მუდმივი შერჩეული ზედაპირის ნაწილისთვის. ამ შემთხვევაში (16.4)-ში მარცხენა ნაწილის ზედაპირული ინტეგრალი ადვილად დაიყვანება <img src= ვექტორის მოდულის ზედაპირის ნაწილის (ან მთელი ზედაპირის) ფართობზე ნამრავლზე. ამის შემდეგ რჩება მხოლოდ სწორად დავითვალოთ მუხტი შემოფარგლული იმ ზედაპირით, რომლშიც ვითვლით ნაკადს.

აქ ამის სადემონსტრაციოდ მოვიყვანთ ორ მაგალითს.

მაგალითი 1. ამოვხსნათ «ნიუტონის ამოცანა» – დავამტკიცოთ, რომ თანაბრად დამუხტული (დიელექტრული) სფეროს გარეთ ველი, არაფრით არ განსხვავდება წერტილოვანი მუხტის ველისგან მანძილებზე, რომელიც მეტია სფეროს R  რადიუსზე

განვსაზღვროთ ასევე ველის დაძაბულობა  სფეროს შიგნით  (r ≤ R) ნებისმიერ წერტილში. ვთვლით, რომ სფეროს შიგნით q  მუხტი განაწილებულია მუდმივი სივრცული სიმკვრივით  \)\dpi{120} \rho\(, სფეროს მასალას აქვს დიელექტრული შეღწევადობა \)\dpi{120} \varepsilon\(.

დაწვრილებით წარმოვაჩინოთ ყველა ძირითადი ნაბიჯი, რაც საჭირო იქნება გაუსის თეორემით („მეორე მეთოდი“) ელექტრული ველის დაძაბულობის გამოსათვლელად.

•1. უნდა გაკეთდეს მუხტის სივრცეში განაწილების სქემატური ნახატი. მასზე მიეთითოს ამოცანის აუცილებელი პარამეტრები - ამ შემთხვევაში ბირთვის რადიუსი R, მუხტის განაწილების მახასიათებელი – მისი სიმკვრივე \)\dpi{120} \rho\(, სფეროს დიელექტრული შეღწევადობა \)\dpi{120} \varepsilon\(. უნდა შემოვიტანოთ შესაბამისი კოორდინატთა სისტემა (მუხტის განაწილების სიმეტრიის გათვალისწინებით), მიეთითოს ნახატზე საკოორდინატო ღერძები (როგორც წესი საკმარისია ხოლმე მხოლოდ ერთი) და ათვლის სათავე.

ჩვენს მაგალითში: მუხტი თანაბრად არის განაწილებული მთელ ბირთვში. მუხტის სიმკვრივე დამოკიდებულია მხოლოდ ცენტრიდან მანძილზე და არ არის დამოკიდებული სივრცეში მიმართულებაზე. ამასთან  \)\dpi{120} \rho \left ( r \right )=const\( როცა r ≤ R და \)\dpi{120} \rho \left ( r \right )=0\( როცა r > R. ძნელი არის იმის მიხვედრა, რომ ამ მდგომარეობისთვის სათანადო იქნება სფერული კოორდინატთა სისტემა.

უფრო მეტიც, რადგან არ გვაქვს უპირატესი სივრცული მიმართულებები, ამიტომ არ დაგვჭირდება პოლარული კუთხეები და რუკაზე საკმარისია მხოლოდ კოორდინატთა სათავის (ცხადია ის უნდა შევუთავსოთ სფეროს ცენტრს და პოლარული ღერძის მითითება.

•2. მოვახდინოთ ველის სტრუქტურის ანალიზი. მუხტის განაწილების კონკრეტულ სიმეტრიაზე დაყრდნობით, გავაკეთოთ დასკვნა ელექტრული ველის დაძაბულობის ველის მიმართულებაზე ბირთვის შიგნით და მის გარეთ ნებისმიერ წერტილში. გავაკეთოთ დასკვნა რომელ კოორდინატებზე შეიძლება იყოს დამოკიდებული დაძაბულობის ვექტორის მოდული და რომლებზე არა. ნახატზე უნდა გაჩნდეს  ვექტორები, რომელთაც ექნებათ საწყისი შესაბამის წერტილებში..

ჩვენს მაგალითში: ცალკეული წერტილოვანი მუხტის ელექტრული ველის თვისებები და სუპერპოზიციის პრინციპი გვაძლევს საშუალებას ვთქვათ, რომ არა მარტო მუხტის სივრცული განაწილებას, არამედ მის ელექტრული ველსაც აქვს რადიალური სიმეტრია. სივრცის ნებისმიერ წერტილში, როგორც ბირთვის შიგნით, ასევე მის გარეთ დაძაბულობის ვექტორი მკაცრად რადიუსის გასწვრივ არის მიმართული (ცენტრიდან, თუ მუხტი დადებითია და ცენტრისკენ, თუ მუხტი უარყოფითია). დაძაბულობის ვექტორი ალბათ დამოკიდებულია ცენტრიდან r მანძილზე, მაგრამ არავითარ შემთხვევაში მიმართულებაზე. ამიტო შემოვიღოთ აღნიშვნა \)\vec{E}(r)\(.

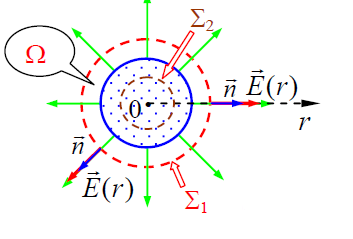
მივაქციოთ ყურადღება, რომ ფრჩხილებს შიგნით არის სწორედ დაშორების მოდული, ანუ მისი რიცხვითი მნიშვნელობა და არა ვექტორი! ნახაზზე ავარჩიოთ ორი ნებისმიერი წერტილი ბირთვის გარეთ და შიგნით და მათთვის მივუთითოთ დაძაბულობის ვექტორის მიმართულებები.

•3. სტრუქტურის ზევით ჩატარებული ანალიზის საფუძველზე ავარჩიოთ \dpi{120} \Sigma\)<strong> შეკრული ზედაპირი</strong> გაუსის თეორემის გამოსაყენებლად</p> <p style=როგორც ადრე აღვნიშნეთ შერჩეული ზედაპირის ნაწილი დაძაბულობის ვექტორისადმი მართობული უნდა იყოს ნაწილი კი პარალელური. დაძაბულობის ვექტორის მოდული უნდა იყოს მუდმივი შერჩეული ზედაპირის ნაწილებისთვის. ნახაზზე უნდა გაჩნდეს ელემენტური ზედაპირებისადმი  ნორმალი ვექტორები  \(\vec{n}\) (ან \(d\vec{S}\), მათ ხომ თანხვედრი მიმართულებები აქვთ).

ჩვენს მაგალითში:  ავარჩიოთ ნახაზზე ორი შეკრული ზედაპირი \dpi{120} \Sigma\(<sub>1</sub> და <img alt=2 – სფეროები, რომელთა ცენტრები ემთხვევა ბირთვის ცენტრს და რადიუსებით r > R და r < R  შესაბამისად. ორი სხვადასხვა ზედაპირი დაგვჭირდა რათა ვიპოვოთ ნაკადი როგორც ბირთვის შიგნით ისე მის გარეთ. საყურადღებოა, რომ არჩეული ზედაპირი არ უნდა ემთხვეოდეს ბირთვის ზედაპირს და საერთოდაც არ უნდა ჰქონდეს გარკვეული რადიუსი, (მოცემულ შემთხვევაში R). ჩვენი ამოცანა ხომ შეადგენს  ფუნქციის პოვნას და არა მისი კონკრეტული მნიშვნელობის პოვნას r-ის რაღაც გარკვეულ მნიშვნელობაზე.

•4. ახლა უნდა გამოვთვალოთ დაძაბულობის ვექტორის ნაკადი \dpi{120} \Sigma\( ზედაპირში. ანუ დავიყვანოთ ზედაპირული ინტეგრალი  <img alt=  ვექტორის მოდულისა და \dpi{120} \Sigma\)  ზედაპირის ნაწილის ან სრული ფართობის ნამრავლზე.</p> <p style=ჩვენს მაგალითში:  რადგან ჩვენ შემთხვევაში  და  ერთნაირი მიმართულებისაა, ამიტომ  ინტეგრალში   სიდიდის ნაცვლად პირდაპირ დავწეროთ დაძაბულობის ვექტორის მოდული და იმის ხაზგასასმელად, რომ ეს სიდიდე არის მხოლოდ r მანძილის ფუნქცია, აღვნიშნოთ ეს სიდიდე ასე – E(r).  r რადიუსის მქონე ზედაპირზე r-ის მნიშვნელობა რა თქმა უნდა მუდმივია და ამიტომ მუდმივია E(r)  ფუნქციის მნიშვნელობაც. ის შეიძლება გავიტანოთ ინტეგრალს გარეთ:

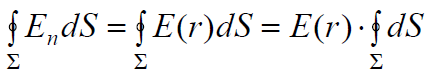
დარჩენილი ინტეგრალი წარმოადგენს \dpi{120} \Sigma\( ზედაპირის ფართობის მათემატიკურად ზუსტი განსაზღვრების ანალიზურ ჩაწერას. ჩვენს შემთხვევაში ორივე არჩეული ზედაპირი <img alt=1 და \(\dpi{120} \Sigma\)2 – სფეროა. სფეროს ზედაპირის ფართობი არის 4πr2. საბოლოოდ

.

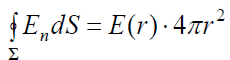
ამ შედეგის სახე ერთნაირია \dpi{120} \Sigma\(<sub>1</sub> და</p> <p style=\dpi{120} \Sigma\)<sub>2</sub> ზედაპირებისთვის. - სხვაობა არის მხოლოდ რადიუსის გარკვეულ დიაპაზონზე მიკუთვნებულობაში.</p> <p style=•5. ამის შემდეგ უნდა გამოვთვალოთ მუხტი, რომელიც შემოიფარგლა  \dpi{120} \Sigma\( <strong><em>ზედაპირით, </em></strong>თავისმხრივ რომლისთვისაც გამოვთვალეთ ნაკადი.</p> <p style=ჩვენს მაგალითში:   აქ კი შედეგის ჩანაწერი განსხვავებული იქნება  \dpi{120} \Sigma\)<sub>1</sub> და <img alt=2 ზედაპირებისთვის. პირველ შემთხვევაში ზედაპირს შიგნით აღმოჩნდება ბირთვის მთელი მუხტი. ის ტოლია ბირთვის მუდმივი მოცულობითი სიმკვრივისა და ბირთვის მოცულობის ნამრავლის:

\dpi{120} \Sigma\)<sub>2</sub> ზედაპირს აქვს რადიუსი <em>r</em><em>, </em>ნაკლები ბირთვის რადიუსზე და ამიტომ ის მოიცავს მის ბირთვის მუხტის მხოლოდ იმ ნაწილს, რომელიც მის შიგნით მოექცა</p> <p style=

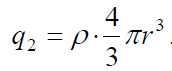
•6. და ბოლოს, დაგვრჩა ჩავწეროთ გაუსის თეორემის შესაბამისი ტოლობა. რადგან  შერჩეული ზედაპირების რადიუსები ნებისმიერი იყო, ამიტომ შედეგი აღწერს სივრცის ნებისმიერ წერტილს და იქნება ზოგადი.

ჩვენს მაგალითში:   ჩავწეროთ გაუსის თეორემის მოპასუხე ორი ტოლობა:

ა) \dpi{120} \Sigma\(<sub>1</sub> <em>ზედაპირისთვის</em> : <a href=my site.

აქედან ვასკვნით, რომ ბირთვის გარეთ ველის დაძაბულობა იცვლება კანონით 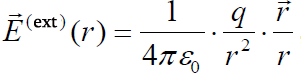, როცა r > R (ველი ბირთვის გარეთ).

იმისათვის რათა ჩავრთოთ ჩაწერაში დაძაბულობის მიმართულებაც, ამიტომ უნდა გადავიდეთ ჩაწერის ვექტორულ ფორმაზე. ამასთან გავითვალისწინოთ, რომ 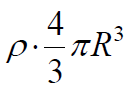  წარმოადგენს ბირთვის სრულ  მუხტს. გვექნება:

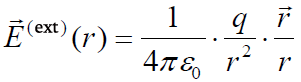, როცა r > R (ველი ბირთვის გარეთ).

ამით ჩვენ დავამტკიცეთ, რომ თანაბრად დამუხტული ბირთვის ველის დაძაბულობა ბირთვის გარეთ ისეთივეა, როგორც წერტილოვანი მუხტისა r მანძილზე, რომლებიც მეტია ბირთვის R რადიუსზე. მას აქვს რადიალური მიმართულება და იცვლება მუხტის თავმოყრის ცენტრიდან დაშორების კვადრატის უკუპროპორციულად.

ბ) 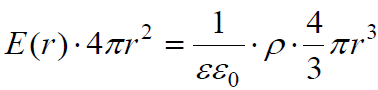\dpi{120} \Sigma\)<sub>2</sub> <em>ზედაპირისთვის</em> :</p> <p style=

აქედან ვასკვნით, რომ ბირთვის შიგნით ველის დაძაბულობა იცვლება კანონით:

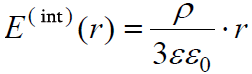  , როცა r ≤ R (ველი ბირთვის შიგნით).

ან ვექტორული ფორმით:

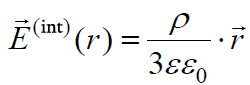, როცა r ≤ R (ველი ბირთვის შიგნით).

როგორც ვხედავთ ბირთვის შიგნით ველის დაძაბულობა მისი ცენტრიდან მანძილის პროპორციულია.

მაგალითი 2. განვსაზღვროთ R რადიუსის მქონე უსასრულოდ გრძელი ცილინდრული ძელაკის ელექტრული ველის დაძაბულობა  ძელაკის ა) შიგნით და ბ) გარეთ. მუხტი თანაბრად იყოს განაწილებული ძელაკის შიგნით \(\dpi{120} \rho\) სივრცული სიმკვრივით; r – დაშორებაა ცილინდრის ღერძიდან, ძელაკის მასალის დიელექტრული შეღწევადობაა \(\dpi{120} \varepsilon\).

1. ამ ამოცანის ნახაზს მოვიყვანთ ოდნავ ქვევით, მას მერე რაც ჩავატარებთ ველის სტრუქტურის ანალიზს და შევარჩევთ \dpi{120} \Sigma\(<sub>1</sub> და <img alt=2 ზედაპირებს.

2. ამ შემთხვევაში მუხტის განაწილებას აქვს „ღერძული სიმეტრია“.

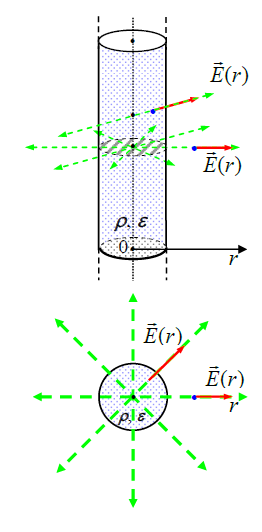
ასეთი სიმეტრია გვკარნახობს ელექტრული ველის შესაბამის სტრუქტურას - ნახაზზე წყვეტილი ხაზებით გამოსახულია ამ ველის ძალწირები ძელაკის ღერძისადმი მართობულ ერთერთ სიბრტყეში. ეს არის ცენტრიდან ყველა მიმართულებით გამომავალი რადიალური სხივები (განსაზღვრულობისათვის მუხტს ვთვლით დადებითად. სივრცის ნებისმიერ წერტილში (ძელაკის როგორც შიგნით, ისე გარეთ) დაძაბულობის ვექტორი მართობულია ძელაკის ღერძისადმი და მიმართულია რადიალურად. დაძაბულობის მოდული, ისევე როგორც წინა მაგალითში, შეიძლება იყოს დამოკიდებული ღერძიდან r დაშორებაზე, მაგრამ არავითარ შემთხვევაში არ იქნება დამოკიდებული აზიმუტურ მიმართულებაზე. ნახაზზე ამას აღვნიშნავთ ასე \(\dpi{120} \vec{E}\left ( r \right )\) (აქაც ფრჩხილებში არის მოდული r).

3. \(\dpi{120} \Sigma\) შეკრული ზედაპირის კრიტერიუმს ამ შემთხვევაში აკმაყოფილებს სწორი წრიული ცილინდრი, რომელიც კოაქსიალურია (ღერძები თანხვედრილია) ძელაკთან. ცილინდრის სიმაღლე ირჩევა ნებისმიერად და აღვნიშნოთ h-ით. ძელაკის გარეთ და შიგნით ველის საპოვნელად კვლავ დაგვჭირდება ორი ჩაკეტილი ზედაპირი – \dpi{120} \Sigma\(<sub>1</sub> და <img alt=2. მათ შორის განსხვავება არის მხოლოდ ის, რომ პირველის რადიუსი  r > R , ხოლო მეორესი r < R (ამას გარდა, მხოლოდ და მხოლოდ ვიზუალური ეფექტისთვის ნახაზზე ოდნავ განსხვავებული სიმაღლეები აქვს ცილინდრებს). კვლავ მივაქციოთ ყურადღება, რომ  ცილინდრების გვერდითა ზედაპირები \dpi{120} \Sigma\(1 და <img alt=r-ის ნებისმიერი მნიშვნელობისთვის. ყოველი ზედაპირო \dpi{120} \Sigma\(<sub>1</sub> და <img alt=2 შედგება ამ შემთხვევაში თავის მხრივ ორი ნაწილისგან – გვერდითა ზედაპირისაგან \dpi{120} \Sigma\(<em><sub>wall</sub> </em>და ფუძე ზედაპირებისგან  <img alt=base.

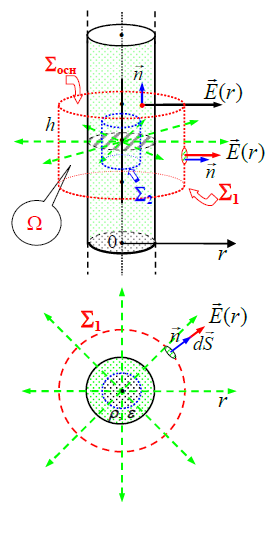
ნახაზზე უნდა მივუთითოთ დაძაბულობის ვექტორი და \(\dpi{120} \vec{n}\) ნორმალი ვექტორი (ან 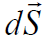) ისევ და ისევ ზედაპირის იმ მცირე dS ელემენტებისთვის.

ელემენტები უნდა აირჩეს ნებისმიერ დაშორებაზე ძელაკის ღერძიდან ორივე ზედაპირისთვის (\dpi{120} \Sigma\(<sub>1</sub> და <img alt=2) როგორც გვერდითა ზედაპირებზე ასევე ფუძეებზე.

4.  სახის ზედაპირული ინტეგრალის გამოთვლის პროცედურა არანაირად არ განსხვავდება \dpi{120} \Sigma\(<sub>1</sub> და <img alt=2 შემთხვევებისთვის. ამიტომ „1“ და „2“ ინდექსებს გამოთვლებისას არ გამოვიყენებთ. დავყოთ ის ორ ნაწილად - გვერდითა ზედაპირი და ფუძეების ზედაპირი:

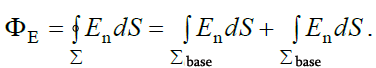
უწინარესად გავითვალისწინოთ, რომ ფუძეებზე 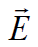 და \(\dpi{120} \vec{n}\) ვექტორები ურთიერთმართობია, ამიტომ ინტეგრალქვეშა გამოსახულება ნულის ტოლია ამ ზედაპირის ნებისმიერი მცირე ელემენტისთვის (Еn = 0). ანუ მთელი ინტეგრალიც  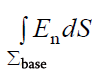არ იძლევა არავითარ წვლილს ნაკადში S ზედაპირში. გვერდითა \dpi{120} \Sigma\(<sub><em>wall</em></sub> ზედაპირზე <img src= და \)\dpi{120} \vec{n}\( თანხვედრო მიმართულებისაა და ამიტომ 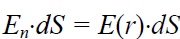. Е(r)  დაძაბულობის მოდული მუდმივია ცილინდრის გვერდითა ზედაპირზე. შეგვიძლია მისი გატანა ინტეგრალიდან:

.\)\oint_{\Sigma _{wall}}^{ }E_{n}dS=E(r)\oint_{\Sigma _{wall}}^{ }dS=E(r)S_{wall}\(

ინტეგრალი 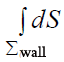 არის  \dpi{120} \Sigma\)<sub><em>wall</em></sub>  ინტეგრების ზედაპირის ფართობი, ანუ ცილინდრისთვის ტოლია – \(\dpi{120} 2\pi rh\). შედეგად <img alt=

.

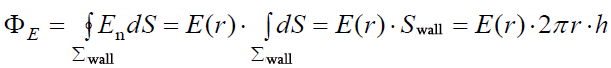ამდენად, შევძელით ზედაპირული ინტეგრალი წარმოგვედგინა სკალარული სიდიდეების ნამრავლის სახით. გარეგნულად ის ერთნაირია 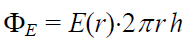\dpi{120} \Sigma\)<sub>1</sub> და \(\dpi{120} \Sigma_{2}\)შემთხვევებისთვის:</p> <p style=

განსხვავება არის მათ მიკუთვნებაში  r -ის ამა თუ იმ დიაპაზონზე მიკუთვნებაში: r > R და r < R.

5. ა) პირველ შემთხვევაში (r > R) 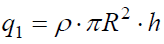\dpi{120} \Sigma\(1 ზედაპირი მოიცავს <em>h</em>  სიგრძის ძელაკის სრულ მუხტს. r სივრცული სიმკვრივის მუდმივობის შემთცვევაში:</p> <p style=.

( \)\dpi{120} \pi R^{2}h\(  - სიმაღლის სწორი წრიული ცილინდრის მოცულობაა).

ბ) 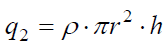\dpi{120} \Sigma\)<sub>2</sub> ცილინდრულ ზედაპირს აქვს ძელაკის რადიუსზე ნაკლები რადიუსი და მოიცავს <em>h</em> სიმაღლის ძელაკის მუხტის მხოლოდ ნაწილს. ეს მუხტი ტოლია</p> <p style=.

6. ახლა უკვე გაუსის თეორემის თანახმად შეიძლება ჩავწეროთ ორი ტოლობა.

ა) \dpi{120} \Sigma\(<sub>1</sub> ზედაპირისთვის: .</p> <p style=ვასკვნით, რომ ძელაკის გარეთ ველის დაძაბულობა იცვლება კანონით:

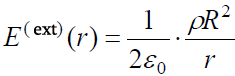   როცა r > R (ველი ძელაკის გარეთ).

ამდენად, ძელაკის გარეთ ველი არის რადიალური მიმართულების და დამუხტული ძელაკის ღერძიდან დაშორების უკუპროპორციულია.

ბ) \dpi{120} \Sigma\)2 ზედაპირისთვის:</p> <p style=

აქედან ვღებულობთ, რომ ძელაკის შიგნით ველი იცვლება კანონით:

,  როცა r ≤ R (ველი ძელაკის შიგნით).

ძელაკის შიგნით ველი იზრდება წრფივად ძელაკის ღერძიდან დაშორებით. შედეგები წარმოდგენილია ნახაზზე.

დასკვნისთვის შევნიშნოთ, რომ არსებითი მომენტი ანალოგიური ამოცანების გადაჭრაში არის    ტიპის ზედაპირული ინტეგრალის შეცვლა სკალარული სიდიდეების ნამრავლით, რაც ზოგად შემთხვევაში შეუძლებელია და შესაძლებელია მხოლოდ სამი ტიპის სიმეტრიების შემთხვევებში – სფერული, ძერძული («აქსიალური») ან ბრტყელი («ბილატერალური» ანუ «სარკული»). დამუხტული სხეულის ნებისმიერი ფორმისთვის ერთადერთი შესაძლებლობა არის „პირველი“ მეთოდის გამოყენება, რომელიც უშუალოდ სუპერპოზიციის პრინციბს ეყრდნობა ან კიდევ ექსპერიმენტული გაზომვა.