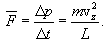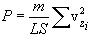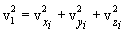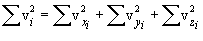იდეალური აირების მოლეკულურ-კინეტიკური თეორიის ძირითადი განტოლება ეწოდება განტოლებას, რომელიც აირის წნევას განსაზღვრავს. მნიშვნელოვანი აქ არის განისაზღვროს ტემპერატურის მოლეკულურ-კინეტიკური არსი. მომავლისთვის დაგვჭირდება მოლეკულების კონცენტრაციის ცნება. კონცენტრაციას ვუწოდებთ მოცულობის ერთეულში მოლეკულების  n რაოდენობას

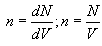(11.1)

პირველი ფორმულა სამართლიანია ყოველთვის, მეორე – მაშინ, როცა მოცულობაში კონცენტრაცია ყველგან ერთნაირია.

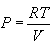
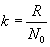
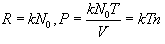
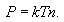კონცენტრაციით შეიძლება ასევე აირის წნევის გამოსახვა  . ადრე შემოტანილი ბოლცმანის მუდმივას გამოყენებით ჩავწერთ . ამდენად, მივიღებთ

(11.2)

აუცილებელია ამავე განტოლების გამოყვანა მოლეკულურ-კინეტიკური თეორიიდანაც, სხვა სიტყვებით რომ ვთქვათ, ვიპოვნოთ აირის წნევა კედელზე. წნევა არის მოლეკულების კედელზე შეჯახებების შედეგი. ერთი წამის განმავლობაში ყველა მოლეკულის მიერ კედელზე გადაცემული იმპულსი არის სწორედ წნევის ძალა, ანუ  PS, სადაც S არის კედლის ფართობი. რადგან მოლეკულის ყოველი შეჯახებისას სრული იმპულსი ინახება, წნევის გამოსათვლელად საჭირო არ არის მოლეკულებს შორის შეჯახებების გათვალისწინება.

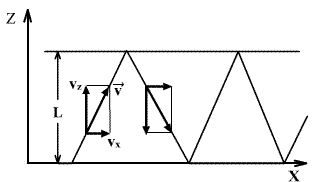
განვიხილოთ მოლეკულა, რომელიც მოძრაობს L მანძილით დაშორებულ კედლებიანი ჭურჭლის კედლებს შორის. ზედა კედელთან შეჯახების შედეგად იცვლება მხოლოდ სიჩქარის v_z მდგენელი. ეს მდგენელი იცლება 2v_z სიდიდით.

მოლეკულის იმპულსის ცვლილება დაჯახებისას (ანუ კედელზე გადაცემული იმპულსი) ტოლია δp=2mv_z . იმპულსის ეს ცვლილება ხდება დროის Δt შუალედში, რომელიც სჭირდება მოლეკულას კედლებზე ორ შეჯახებას შორის და ტოლია  .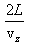

ამდენად, ერთი მოლეკუა კედელზე მოქმედებს საშუალო ძალით

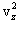
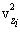
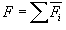
სხვადასხვა მოლეკულებს სხვადასხვა სიჩქარეები აქვთ, ამიტომ -ს ნაცვლად უნდა ჩავწეროთ  , სადაც i – მოლეკულის ნომერია. ყველა მოლეკულის მხრიდან სრული ძალა იქნება  . იმისათვის რათა ვიპოვნოთ წნევა, ძალა უნდა გავყოთ კედლის S ფართობზე:

ახლა ჩავწეროთ

ავჯამოთ ყველა N მოლეკულით

x,y,z ღერძთა თანაბარუფლებიანობის გამო თერმოდინამიკური წონასწორობის დროს მარჯვენა სამი ჯამი (მოლეკულების დიდი რიცხვის შემთხვევაში) ერთმანეთის ტოლია, საიდანაც

.

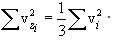
შემოვიღოთ საშუალო კვადრატული სიჩქარის ცნება (მას ასევე სითბურ სიჩქარეს უწოდებენ v_i ). ამისთვის აუცილებელია სიჩქარის საშუალო კვადრატის მოძებნა. ის, ცხადია, ტოლია

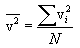(11.3)

გამოსახულება (11.3) სრულიად ანალოგიურია საშუალო არითმეტიკული სიჩქარის გამოსახულებისა

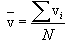(11.4)

მხოლოდ (11.4)-ში იკრიბება მოლეკულების სიჩქარეების აბსოლუტური სიდიდეები, ხოლო (11.3)-ში – სიჩქარის კვადრატები.

საშუალოკვადრატული, ანუ სითბური სიჩქარე ეწოდება (11.3) გამოსახულების კვადრატულ ფესვს:

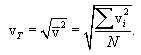(11.5)

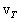
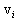
აღვნიშნოთ, რომ  ყოველთვის მეტია საშუალო არითმეტიკულ სიჩქარეზე (11.4). ამას ადვილად შევამოწმებთ, თუ  -ს ნაცვლად ჩავსვამთ ნებისმიერ (არატოლ) რიცხვებს.

აირების მკთ განტოლების გამოყვანას დავუბრუნდეთ და (11.3)-ის გამოყენებით ჩავწეროთ:

.

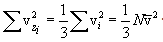
მიღებული გამოსახულება ჩავსვათ P-ს გამოსახულებაში, მივიღებთ

.

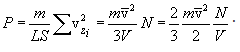
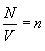
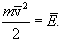
ბოლოს, იმის გათვალისწინებით, რომ  არის კონცენტრაცია, და რომ _{კინ გად} არის მოლეკულების გადატანითი მოძრაობის საშუალო კინეტიკური ენერგია, მივიღებთ

\(P=\frac{2}{3}n\bar{E}_{k}\)

(11.6)

სწორედ ეს არის იდეალური აირის მკთ ძირითადი განტოლება ის ასე იკითხება: აირის წნევა ერთეულოვან მოცულობაში მოქცეული მოლეკულების გადატანითი მოძრაობის კინეტიკური ენერგიის 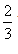-ის ტოლია.

(11.6)-ის (11.2)-თან შედარებით, მივიღებთ ძალიან მნიშვნელოვა ტოლობას

\(\bar{E}_{k}=\frac{3}{2}kT\)

(11.7)

ეს გამოსახულება ხსნის ტემპერატურის ცნების მოლეკულურ-კინეტიკურ არსს.

ტემპერატურა – ეს არის მოლეკულების მოძრაობის საშუალო კინეტიკური ენერგია (გამოსახული სხვა ერთეულებში).

ამ განსაზღვრებაში ძალიან მნიშვნელოვანია სიტყვა "საშუალო". თუ აირს ამოვაცლით ყველაზე ნელ მოლეკულას, ყველა მოლეკულის სრული კინეტიკური ენერგია მცირდება, მაგრამ ტემპერატურა იზრდება, რადგან იზრდება საშუალო კინეტიკური ენერგია.

ჩავწეროთ

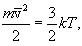(11.8)

აქედან ვიპოვნით მოლეკულის საშუალოკვადრატულ სიჩქარეს

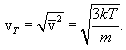(11.9)

ეს სიჩქარე ტემპერატურიდან კვადრატული ფესვის პროპორციულია.

(11.9) შეიძლება ასე ჩავწეროთ

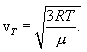(11.10)

ჟანგბადის მოლეკულისთვის (μ=0,032 კგ/მოლი) როცა Т=300К v_Т=483 მ/წმ. წყალბადის მოლეკულისთის (μ=0,002 კგ/მოლ) ამავე ტემპერატურაზე სიჩქარე ტოლია v_Т=1932 მ/წმ, ანუ ის მეტია ჟანგბადის მოლეკულის სიჩქარეზე 4-ჯერ.

ძალიან მნიშვნელოვანია ის გარემოება, რომ თერმოდინამიკური წონასწორობის პირობებში მოლეკულის საშუალო კინეტიკური ენერგია (11.8) არ არის მოლეკულის მასაზე დამოკიდებული. თუ შევურევთ რამოდენიმე აირს, მაგალითად Н₂, О₂ და წყალბადის მოლეკულაზე ასჯერ უფრო მძიმე მოლეკულებიან აირს მაშინ თერმოდინამიკური წონასწორობის პირობებში ყველა გაზის საშუალო კინეტიკური ენერგია იქნება ერთმანეთის ტოლი. მძიმე მოლეკულები იმოძრავებენ მცირე სიჩქარეებით, ისეთით, რომ მათი საშუალო კინეტიკური ენერგია ზუსტად ტოლი იყოს მსუბუქი მოლეკულების საშუალო კინეტიკური ენერგიისა.

სითხეში ბროუნის ნაწილაკების საშუალო კინეტიკური ენერგი, ამ ნაწილაკების უზარმაზარი მასის მიუხედავად (მოლეკულების მასასთან შედარებით) ისეთივეა როგორის მოლეკულებისა.

შეიძლება განვიხილოთ მძიმე და მსუბუქი აირები, როგორც ორი ერთმანეთთან თერმოდინამიკურ წონასწორობაში მყოფი სისტემა. თერმოდინამიკური წონასწორობა გულისხმობს ამ სისტემების ტემპერატურების ტოლობას. წინააღმდეგ შემთხვევაში სითბო გადაეცემა უფრო ცხელი სისტემიდან უფრო გრილ სისტემას.