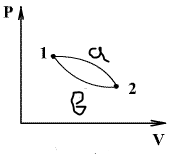
განვიხილოთ შექცევადი პროცესი 1a2 და 2b1 გზაზე. რადგან 1a2b1 პროცესი არის შექცევადი, ამიტომ მისთვის სამართლიანია კლაუზიუსის ტოლობა
\(\oint_{L}^{ }\frac{\delta Q}{T}=0\)
დავყოთ ეს ინტერვალი ორ გზად 1a2 და 2b1
\(\int_{1a}^{2}\frac{\delta Q}{T}+\int_{2b}^{1}\frac{\delta Q}{T}=0\)
რადგან
\(\int_{2b}^{1}\frac{\delta Q}{T}=-\int_{1b}^{2}\frac{\delta Q}{T}\)
ამიტომ
\(\int_{1a}^{2}\frac{\delta Q}{T}=\int_{1b}^{2}\frac{\delta Q}{T}\)
ამდენად, დაყვანილი სითბოების ჯამი ერთი მდგომარეობიდან მეორეში გადასვლისას არ არის დამოკიდებული გადასვლის ფორმაზე (გზის ფორმაზე) შექცევადი პროცესების შემთხვევაში. ეს არის კლაუზიუსის თეორემა.