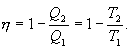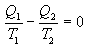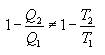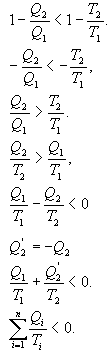განვიხილოთ შექცევადი და შეუქცევადი კარნოს ციკლები
შექცევადი კარნოს ციკლი. შექცევადი კარნოს ციკლისთვის მარგი ქმედების კოეფიციენტი ნებისმიერი ზემოთ მიღებული ფორმულით შეიძლება გამოითვალოს
აქედან
ან 
- სთბოს რაოდენობაა, რომელიც სისტემას მიეწოდება 1 მდგომარეობიდან 2 მდგომარეობაში გადასვლისას. 
- 3-4 იზოთერმული პროცესის განმავლობაში წართმეული სითბო. ანუ სითბოს წართმევის შემთხვევისთვის შეიძლება ითქვას, რომ სისტემას მიეწოდა 
სითბო. მაშინ
 |
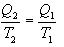
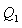
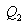
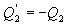
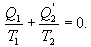(10.25) |
სისტემაზე მიწოდებული სითბოს ფარდობა იმ ტემპერატურასთან, რომელზეც ეს ხდება, ეწოდება დაყვანილი სითბო. ამდაგვარად,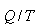 
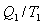
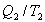
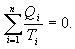არის დაყვანილი სითბო, რომელიც გადაეცემა სისტემას. 
- დაყვანილი სითბო I პროცესში. 
- დაყვანილი სითბო II პროცესში. 2-3 და 4-1 უბნებზე Q=0. შესაბამისად, ეს არის სრული სითბო, რომელიც მოიცავს კარნოს ციკლს. ამდენად, შექცევადი კარნოს ციკლისთვის
 |
(10.26) |
რადგან შეიძლება ნებისმიერი შეკრული ციკლი წარმოვადგინოთ, როგორც უსასრულო ჯამი კარნოს ციკლებისა, ამიტომ ნებისმიერი შეკრული შექცევადი ციკლისთვის გამოსახულება (10.26) იქნება სამართლიანი და ის შეიძლება ჩავწეროთ ასე
| \(\oint_{L}^{ }\frac{\delta Q}{T}=0\) | (10.27) |
უკანასკნელ თანაფარდობას უწოდებენ კლაუზიუსის ტოლობას.
კარნოს შეუქცევადი პროცესი. ამ შემთხვევაში
და ყველა ტოლობა გარდაიქმნება უტოლობებად
| \(\oint_{L}^{ }\frac{\delta Q}{T}< 0\) | (10.28) |
(10.28) განტოლებას ეწოდება კლაუზიუსის უტოლობა.
გავაერთიანებთ რა (10.27)-სა და (10.28)-ს, მივიღებთ
| \(\oint_{L}^{ }\frac{\delta Q}{T}\leq 0\) | (10.29) |
ამდენად, ნებისმიერი ციკლის დაყვანილი სითბოების ჯამი ნულის ტოლია (შექცევადი პროცესი) ან ნულზე ნაკლებია (შეუქცევადი პროცესი).