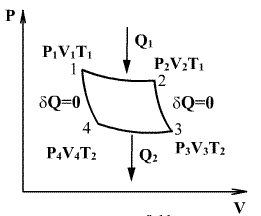
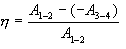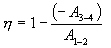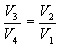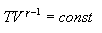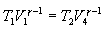სითბური ძრავების მუშაობის ანალიზით, ფრანგი ინჟინერი სადი კარნო 1924 წელს მივიდა დასკვნამდე, რომ ყველაზე ხელსაყრელი წრიული პროცესი არის შექცევადი წრიული პროცესი, რომელიც შედგება ორი იზოთერმული და ორი ადიაბატური პროცესისგან, რადგან ისი ხასიათდება უდიდესი მარგი ქმედების კოეფიციენტით. ამ პროცესს ეწოდა კარნოს ციკლი. კარნოს პირდაპირ ციკლში მუშა სხეული იზოთერმულად, ხოლო შემდეგ ადიაბატურად ფართოვდება, რის შემდეგაც ისევ იზოთერმულად (უფრო დაბალ ტემპერატურაზე) და შემდეგ ადიაბატურად იკუმშება. ანუ კარნოს ციკლი შემოსაზღვრულია ორი იზოთერმითა და ორი ადიაბატით.

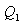
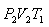
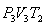
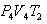
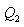
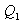
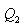
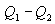
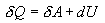
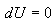
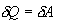
იზოთერმული გაფართოებისას გამათბობელს წაერთმევა  სითბო (1-2 უბანზე). ამის შედეგად აირის ტემპერატურა ნარჩუნდება უცვლელი. შესაბამისად, წერტილი 2-ის პარამეტრები იქნება . 2-3  უბანზე ხდება ადიაბატური გაფართოება. აირის შინაგანი ენერგია მცირდებაბდა მისი ტემპერატურა ეცემა Т₂-მდე. წერტილი 3-ის პარამეტრები იქნება  . 3-4 უბანზე აირი იზოთერმულად იკუმშება. წერტილი 4-ის პარამეტრები არის  . ამ დროს გამოყოფილი სითბოს  ართმევს მაცივარი. უბანი 4-1 არის ადიაბატური შეკუმშვა საწყის მდგომარეობამდე, რომელიც წერტილ 1-ს შეესაბამება. ამდენად, დასრულდა კარნოს ციკლი “1-2-3-4-1" და შედეგად გამათბობელმა გადასცა აირს  სითბო, ხოლო მაცივარმა წაართვა  სითბო. სხვაობა განსაზღვრავს აირის სასარგებლო მუშაობას ერთი ციკლის განმავლობაში, რადგან თერმოდინამიკის პირველი კანონის თანახმა  , მაგრამ წრიული პროცესისთვის  და ამიტომ  .

სასარგებლო მუშაობის ფარდობა გამათბობლის მიერ დახარჯულ ენერგიასთან განსაზღვრავს სითბური მანქანის მარგი ქმედების კოეფიციენტს (მქკ):

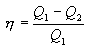(10.23)

ეს ფორმულა სამართლიანია ყველა შექცევადი და არაშექცევადი პროცესისთვის.

განვსაზღვროთ შექცევადი პროცესის კარნოს ციკლის მქკ. სითბო მიეწოდება უბანზე  1-2 და წაერთმევა უბანზე 3-4. იზოთერმული პროცესისთვის შინაგანი ენერგია U=const და მთელი მიწოდებული სითბო იხარჯება მუშაობაზე .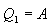

მაშინ

ანუ

იზოთერმული პროცესისთვის მუშაობა
 
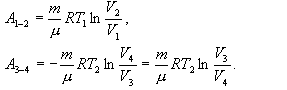
უკანასკნელი გამოსახულებების გათვალისწინებით

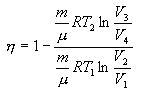(10.24)

ვაჩვენოთ, რომ

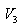
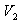
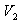
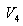
რადგან პროცესები უბნებზე 2-3 და 1-4 ადიაბატურებია,  და  და  და  კავშირების განსასაზღვრად გამოვიყენოთ პუასონის განტოლება შემდეგი სახით 

შესაბამისად,

და

გავყოთ ეს განტოლებები და მივიღებთ

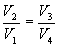
მაშინ მქკ-ს გამოსახულება (10.24) მიიღებს სახეს

ეს ფორმულა სამართლიანია მხოლოდ შექცევადი კარნოს ციკლისთვის.

კარნოს თეორემები.

1. ყველა კარნოს ციკლით მომუშავე შექცევად მანქანას, დამოუკიდებლად მუშა სხეულის ბუნებისა, აქვს ერთნაირი მქკ, იმ პირობით თუ მათ აქვთ საერთო გამათბობელი და მაცივარი.

2. თუ ორ სითბურ მანქანას აქვთ საერთო გამათბობელი და და მაცივარი და მათგან ერთი არის შექცევადი, ხოლო მეორე შეუქცევადი, მაშინ შექცევადის მქკ მეტია შეუქცევადის მქკ-ზე

η_შექც>η_{შეუქც}