მოამზადეს: დავით ხუციშვილმა და ირაკლი მღებრიშვილმა

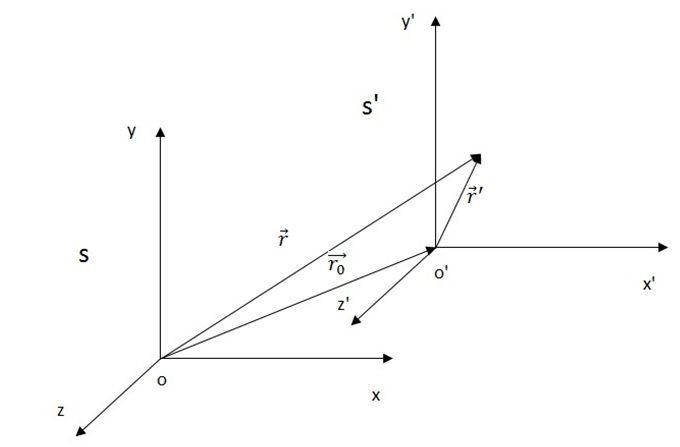
ნიუტონის I და II კანონები მართებულია მხოლოდ ათვლის ინერციულ სისტემებში. ვთქვათ, S წარმოადგენს ათვლის ინერციულ სისტემას, ხოლო S' - სისტემას, რომელიც მოძრაობას S სისტემის მიმართ \(\vec{v}_{0}\) სიჩქარით, ისე რომ მისი ღერძები S სიტემის ღერძების პარალელურია. ანუ, S' სისტემა მოძრაობს S სისტემის მიმართ გადატანით, \(\vec{v}_{0}\) სიჩქარით (ნახ. 1).

ნახ. 1

თუ ნებისმიერი M წერტილის რადიუს–ვექტორებს S და S' სისტემებში შესაბამისად აღვნიშნავთ \(\vec{r}\) და \(\vec{r}_{'}\)– ით, მაშინ ნახაზიდან გვექნება, რომ

\(\vec{r}=\vec{r}^{'}+\vec{r}_{0}\)

თუ ამ ტოლობას დროით გავაწარმოებთ, მივიღებთ

\(\vec{v}=\vec{v}^{'}+\vec{v}_{0}\)           (1)

სადაც \(\vec{v}\) და \(\vec{v}'\) მატერიალური M წერტილის სიჩქარეებია შესაბამისად S და S' სისტემათა მიმართ.

(1) წარმოადგენს სიჩქარეთა შეკრების გალილეის კანონს და ამ ტოლობის დროით გაწარმოება გვაძლევს დამოკიდებულებას S და S' სისტემებში M წერტილის აჩქარებებს შორის:

\(\vec{a}=\vec{a}^{'}+\vec{a}_{0}\)           (2)

ა) ვთქვათ S' სისტემა ინერციულია. ეს ნიშნავს, რომ იგი მოძრაობს ინერციული S სისტემის მიმართ თანაბრად და წრფივად, ანუ \(\vec{a}_{0}=\frac{\mathrm{d} \vec{v}_{0}}{\mathrm{d} t}=0\), მაშინ (2)–დან

\(\vec{a}=\vec{a}^{'}\)                 (3)

ორივე სისტემაში მატერიალურ წერტილზე მოქმედი ძალები ერთნაირია \(\vec{F}=\vec{F}^{'}\), ვინაიდან მოცემულ წერტილზე მოქმედი ძალა განისაზღვრება მის გარემომცველ სხეულთა მდებარეობით და მოქმედების ხასიათით, რაც კოორდინატთა სისტემის შერჩევაზე არ არის დამოკიდებული.

მივიღეთ, რომ თუ ერთ–ერთ ინერციულ სისტემაში წერტილის აჩქარება გამოწვეულია მხოლოდ გარემომცველ სხეულებთან მისი ურთიერთქმედებით, მაშინ ნებისმიერ სხვა ინერციულ სისტემაში მასზე იმოქმედებს იგივე ძალა და მიანიჭებს მას იმავე აჩქარებას. თუ კერძოდ, S სისტემაში M მატერიალურ წერტილზე მოქმედი ძალა ნულის ტოლია, \(\vec{F}=0\) და მაშასადამე \(\vec{a}=0\), მაშინ S' სისტემაშიც \(\vec{F}'=0\) და \(\vec{a}'=0\). აქედან გამომდინარეობს დასკვნა, რომ ინერციული S და S' სისტემები მექანიკური თვალსაზრისით სრულიად ეკვივალენტურია.

ბ) ვთქვათ, S' სისტემა არაინერციულია, ანუ აჩქარებული, \(\vec{v}_{0}\)≠const და მაშასადამე \(\vec{a}_{0}\) ≠ 0. მაშინ (2)–დან

\(\vec{a}^{'}=\vec{a}-\vec{a}_{0}\)

ხოლო

\(m\vec{a}^{'}=m\vec{a}-m\vec{a}_{0}\)

მაგრამ \(m\vec{a}=\vec{F}'=\vec{F}\) ამიტომ გამოდის, რომ

\(m\vec{a}^{'}=\vec{f}'-m\vec{a}\)    (4)

ე.ი. არაინერციულ სისტემაში ნიუტონის მეორე კანონი მართებული არ რჩება (m მასის მატერიალურ წერტილზე ამ სისტემაში მოქმედი ძალა \(\vec{F}'\) არ უდრის მასისა და ამ სიტემაში წერტილის აჩქარების ნამრავლს, \(m\vec{a}^{'}\neq \vec{f}'\))

აქედან გამომდინარეობს ორი დებულებიდან ერთ–ერთის დაშვების აუცილებლობა: ან არაინერციულ სისტემაში წერტილის აჩქარება გამოწვეულია არამარტო ძალებით, ან აჩქარება პროპორციულია მოქმედი ძალების ტოლქმედის, მაგრამ ამ ძალების გამომწვევი მიზეზი, სხეულთა მოქმედების გარდა, შეიძლება იყოს სხვა რაღაც, რაც საჭიროებს გათვალისწინებას.

რადგან პირველი დაშვება დაკავშირებულია მექანიკის ძირითადი კანონების უარყოფასთან, ამიტომ უფრო მიზანშეწონილია მეორე დაშვება: (4)–ის საფუძველზე უნდა დავუშვათ, რომ არაინერციულ S' სისტემაში, გარდა გარემომცველი სხეულების ურთიერთქმედებით განპირობებულ \(\vec{F}'\) ძალისა, M მატერიალურ წერტილზე მოქმედებს აგრეთვე ძალა

\(\vec{F}_{i}=m(-\vec{a}_{0})\)

გამოწვეული თვით სისტემის აჩქარებით. ასეთ \(\vec{F}_{i}\) ძალას ინერციის ძალა ეწოდება. უნდა აღინიშნოს, რომ ინერციის ძალა არ გამოსახავს განხილულ მატერიალურ წერტილზე სხვა სხეულების მოქმედებას და გამოწვეულია თვით ათვლის სისტემის აჩქარებით. ინერციის ძალა უდრის მატერიალური წერტილის მასისა და სისტემის აჩქარების ნამრავლს, აღებულს მოპირდაპირე ნიშნით.

განვიხილოთ ინერციის ძალათა მოქმედების რამდენიმე მაგალითი.

განვიხილოთ დედამიწის მიმართ თანაბარაჩქარებულად და წრფივად მოძრავი ურიკა, რომლის ზედაპირზე მოთავსებულია სხეული. წარმოვიდგინოთ, რომ სხეულიც ურიკასთან ერთად მოძრაობს. სხეულზე მოქმედი ძალებია სიმძიმის ძალა, ურიკის მხრიდან მოქმედი ხახუნის ძალა და ურიკას რეაქციის ძალა (იხ. ნახ.2). დედამიწასთან დაკავშირებულ ათვლის სისტემაში სამი ძალის ტოლქმედი სხეულს ანიჭებს აჩქარებას და სხეული ურიკასთან ერთად მოძრაობს. განვიხილოთ სხეულის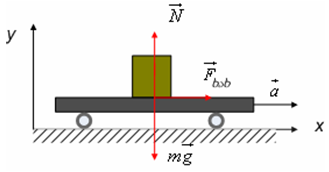 მოძრაობა ურიკასთან დაკავშირებულ ათვლის სისტემაში. ამ სისტემაში სხეული უძრავია მიუხედავად იმისა, რომ სხეულზე ჰორიზონტალური მიმართულებით მოქმედი ხახუნის ძალა არ არის გაწონასწორებული რომელიმე სხვა ძალით (ვერტიკალური მიმართულებით რეაქციის და სიმძიმის ძალები ერთმანეთს აბათილებენ). მაშასადამე ნიუტონის კანონის გამოყენებამ მიგვიყვანა წინააღმდეგობამდე. თუ წარმოვიდგენთ, რომ ურიკას ზედაპირი აბსოლუტურად გლუვია და ხახუნს ადგილი არ აქვს, მაშინ სხეული ურიკის მიმართ იმოძრავებს საპირისპირო მიმართულებით აჩქარებით მაშინ, როდესაც სხულზე მოქმედი სამი ძალიდან მხოლოდ ორი ძალა (სიმძიმის და რეაქციის) აბათილებს ერთმანეთს. ამ შემთხვევაშიც ნიუტონის კანონი  რეალობასთან წინააღმდეგობაში მოდის. ამრიგად, ეს მარტივი მაგალითი გვიჩვენებს, რომ ნიუტონის კანონები აჩქარებულად მოძრავ ათვლის სისტემაში ირღვევა.

ათვლის ინერციულ სისტემებში, როგორც ვიცით, აჩქარების გამომწვევ მიზეზს წარმოადგენს ძალა ან ძალების ტოლქმედი. ძალის საშუალებით ჩვენ რაოდენობრივად აღვწერთ სხეულების ურთიერთქმედებას. ძალის წარმოქმნის სხვა რაიმე მიზეზი, გარდა სხეულთა ურთიერთქმედებისა, არარსებობს. გარდა ამისა ორი სხეული ერთმანეთთან ურთიერთქმედებს სიდიდით ტოლი და ურთიერთსაპირისპიროდ მიმართული ძალებით. ათვლის არაინეციულ სისტემებში ამ დებულებების შენარჩუნება არ ხერხდება.

განვიხილოთ სხეულის მოძრაობა უძრავი ღერძის გარშემო თანაბრად მბრუნავ წრიულ სიბრტყეზე მყოფი დამკვირვებლის თვალსაზრისით (იხ.ნახ.3).

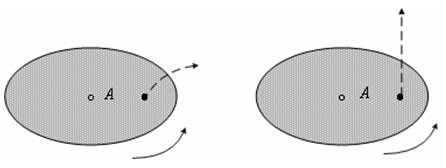
ეს დამკვირვებელი ცხადია არის აჩქარებულად მოძრავი და მაშასადამე ათვლის არაინერციული სისტემა. ამ დამკვირვებლისთვის დანარჩენი სამყარო მოძრაობს მის გარშემო. დაუშვათ მან ფრთხილად დადო ბურთი მბრუნავ სიბრტყეზე ისე, რომ სიბრტყის მიმართ საწყისი სიჩქარე არ მიანიჭა. სიბრტყე ჩავთვალოთ აბსოლუტურად გლუვად და ხახუნი არ მივიღოთ მხედველობაში. ნიუტონის პირველი კანონის თანახმად საწყის მომენტში უძრავად მყოფი ბურთი უნდა  დარჩეს უძრავი: ამ სხეულზე მოქმედი სიმძიმის და რეაქციის ძალები ერთმანეთს აბათილებენ. სხვა ძალა კი სხეულზე არმოქმედებს. სიბრტყეზე მყოფი დამკვირვებელი კი ხედავს, რომ ბურთი იწყებს მოძრაობას აჩქარებულად. უძრავი დამკვირვებელი, რომლის მიმართ სიბრტყე ასრულებს ბრუნვით მოძრაობას, ხედავს, რომ სხეულს აქვს ბურთის დადების წერტილის წირითი სიჩქარის ტოლი საწყისი სიჩქარე, რომლითაც სხეული აგრძელებს წრფივად და თანაბრად მოძრაობას იმ წრეწირის მხების გასწვრივ, რომელსაც ეკუთვნის ეს წერტილი. როგორც ვხედავთ ნიუტონის პირველი კანონი ირღვევა მბრუნავ სიბრტყესთან დაკავშირებულ ათვლის სისტემაში.

იმისათვის, რომ ნიუტონის კანონების სამართლიანი იყოს ათვლის არაინერციულ სისტემებშიც, უნდა დავუშვათ, რომ აჩქარებას სხეულების ურთიერთქმედების გარდა იწვევს რაღაც სხვა მიზეზიც, რომელსაც არაფერი აქვს საერთო სხეულების ურთიერთქმედებასთან და მაშასადამე ძალებთან ჩვეული აზრით. თუმცა მოხდა ისე, რომ დაშვებული იქნა ახალი ტიპის ძალის არსებობა, რომელსაც ისეთივე კავშირი აქვს აჩქარებასთან როგორც სხვა, ბუნებაში არსებულ რეალურ ძალებს. ამ ძალის შემოტანით შესაძლებელი გახდა ნიუტონის მეორე კანონის შენარჩუნება  და მას ინერციის ძალაეწოდა. ეს ძალა არ არის დაკავშირებული სხეულების ურთიერთქმედებასთან. ეს ძალა არის ფიქტიური ძალა, რომლის არსებობა დაშვებულია მხოლოდ ათვლის არაინერციულ სისტემებში. ამ ძალების არსებობა განპირობებულია მხოლოდ იმით, რომ არაინერციული ათვლის სისტემა აჩქარებულად მოძრაობს. მისმა შემოტანამ შესაძლებელი გახადა ნიუტონის პირველი და მეორე კანონების გამოყენება ათვლის არაინერციულ სისტემებშიც. ნიუტონის მესამე კანონი ასეთი სისტემებისთვის კვლავ არასამართლიანია –ი ნერციის უკუქმედება არ არსებობს.

ინერციის ძალის გათვალისწინებით  ნიუტონის მეორე კანონი სხეულისთვის, რომელიც მოძრაობს ათვლის არაინერციული სისტემის მიმართ, რაღაც a₀ აჩქარებით, ჩაიწერება შემდეგი სახით

F + F_in = ma₀,

სადაც F არის სხეულების ურთიერთქმედებით გამოწვეული ძალების ტოლქმედი, ეს უკანასკნელი სხეულს ინერციული ათვლის სისტემის მიმართ ანიჭებს a აჩქარებას და ე.ი. F=ma. ასეთნაირად ჩაწერილი განტოლებიდან ინერციის ძალისთვის მივიღებთ:

F_in = m(a₀-a)

 ადვილი დასანახია, რომ სიდიდე a'=a₀-a არის აჩქარება, რომლითაც ათვლის არაინერციული სისტემა მოძრაობს ათვლის ინერციული სისტემის მიმართ (სხეულის აჩქარება a ათვლის ინერციული სისტემის მიმართ წარმოადგენს ათვლის არაინერციული სისტემის მიმართ მისი აჩქარების a₀ და ათვლის ინერციული სისტემის მიმართ არაინერციული სისტემის აჩქარების a' ვექტორულ ჯამს). ამრიგად ინერციის ძალას აჩქარებულად მოძრავ ათვლის სისტემაში აქვს შემდეგი სახე:

F_in = -ma'

 ეს ნიშნავს, რომ ინერციის ძალა სხეულს ანიჭებს იმ აჩქარების საპირისპიროდ მიმართულ აჩქარებას, რომლითაც ათვლის არაინერციული სისტემა მოძრაობს ათვლის ინერციული სისტემის მიმართ. თუ სხეული უძრავია ათვლის არაინერციულ სისტემაში (ან მოძრაობს თანაბრად და წრფივად), მაშინ a'=a (სხეულიც მოძრაობს იგივე აჩქარებით ათვლის ინერციულისისტემის მიმართ, როგორითაც ათვლის არაინერციული სისტემა), ხოლო F_in = -ma'. თუ მიუყენებთ ნიუტონის მეორე კანონს ასეთი სახით ნახ. 3–ზე განხილულ მაგალითს ხახუნის გაუთვალისწინებლად მაშინ სხეულის მოძრაობა ურიკაზე ურიკის მოძრაობის საპირისპირო მიმართულებით გამოწვეულია მხოლოდ ინერციის ძალით (ვგულისხმობთ, რომ სიმძიმის და რეაქციის ძალები ერთმანაეთს აბათილებენ) და ეს ძალა ანიჭებს სხეულს ურიკის აჩქარების საპირისპიროდ მიმართულ აჩქარებას. ათვლის ინერციული სისტემის მიმართ კი ეს სხეული იქნება უძრავი.

 

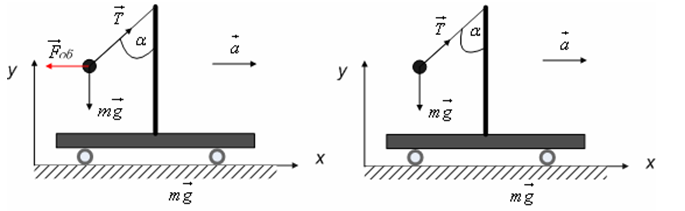
განვიხილოთრამდენიმემაგალითიდა ვნახოთთუროგორშეიძლებაერთიდაიგივემოძრაობააღვწეროთათვლისროგორცინერციულ,       ასე არაინერციულ სისტემებში. ვთქვათ ურიკა მასზე უძრავად დამაგრებული ვერტიკალური ღეროთი მოძრაობს მუდმივი a აჩქარებით (იხ. ნახ. 4). ღეროზე ჩამოკიდებულია ძაფზე დამაგრებული m  მასის ბურთულა. ურიკას აჩქარებული მოძრაობა გამოიწვევს ძაფის გადახრას ვერტიკალის მიმართ რაღაც \(\alpha\) კუთხით, ურიკასთან დამაგრებული ათვლის არაინერციულ სისტემაში ბურთულაზე მოქმედებს სამი ძალა: სიმძიმის ძალა, ძაფის დაჭიმულობის ძალადა ინერციის ძალა. რადგან ბურთულა ურიკის მიმართ  უძრავ მდგომარეობაშია (ნახ. 4), ნიუტონის მეორე კანონი ამ სისტემაში ჩაიწერება ასე:

F_in+T+mg=0

თუ გავითვალისწინებთ ინერციის ძალის მნიშვნელობას, მაშინ

-ma+T+mg=0

რაც ემთხვევა ნიუტონის მეორე კანონს ინერციული ათვლის სისტემის მიმართ:

T+mg=ma

განვიხილოთ ისევ მბრუნავი სიბრტყე და მასზე მოთავსებული სხეული. მხოლოდ გავითვალისწინოთ ხახუნი სხეულსა და სიბრტყეს შორის. ვთქვათ სიბრტყის კუთხური სიჩქარე არ არის საკმარისი იმისთვის, რომ სხეული მოწყდეს ზედაპირს. მა

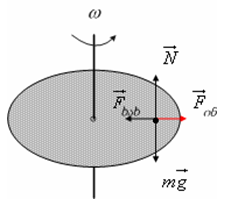
შინ სხეული ბრუნავს სიბრტყესთან ერთად. უძრავი დამკვირვებლისთვის         (ათვლის          ინერციულ სისტემაში) ნიუტონის მეორე კანონის თანახმად N+mg+Fხახ= ma სხეულს აქვს          ცენტრისკენული აჩქარება, რომელსაც მას რეალურად ანიჭებს ხახუნის ძალა (ვერტიკალური მიმართულებით აჩქარება არ გვაქვს და ძალები ერთმანეთს აბათილებენ). სიბრტყეზე მყოფი დამკვირვებლისთვის (ათვლის არაინერციული სისტემა) სხეული უძრავია. ამიტომ ნიუტონის პირველი კანონის თანახმად ინერციის ძალის გათვალისწინებით

N+ mg+ Fხახ+ Fინ= 0

სიმძიმის და რეაქციის ძალები აწონასწორებენ ერთმანეთს, ხოლო ჰორიზონტალური მიმართულებით ინერციის ძალა აწონასწორებს ხახუნის ძალას, ანიჭებს რა სხეულს ცენტრისკენული აჩქარების საპირისპიროდ მიმართულ აჩქარებას.

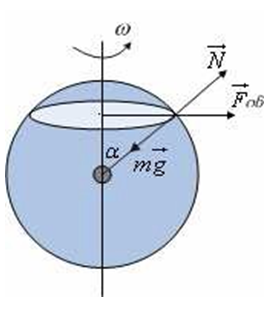
როდესაც ვსაუბრობთ ათვლის ინერციულ სისტემებზე, ვგულისხმობთ, რომ დედამიწის ბრუნვითი მოძრაობის და მისი ცენტრისკენული აჩქარების უგულებელყოფა შესაძლებელია. თუ მკაცრად ვიმსჯელებთ, მაშინ დედამიწასთან დაკავშირებული ათვლის სისტემა არაინერციულია (იხ. ნახ. 6) და აუცილებელია ინერციის ძალის გათვალისწინება სიმძიმის და დედამიწის რეაქციის ძალებთან ერთად. ინერციის ძალა სხეულს ანიჭებს აჩქარებას, რომელიც მიმართულია ცენტრიდან და სიდიდით ტოლია

F_ინ= m\(\omega ^{2}\) r

სადაც r არის აღნიშნულ განედზე მბრუნავი სხეულის ტრაექტორიის რადიუსი. ინერციის ძალის მოქმედება იწვევს იმას, რომ   სხეულისწონა   ამწერტილში ნაკლებია სიმძიმის ძალაზე.

თუ სხეული მბრუნავ სისტემაშია მოთავსებული, მაშინ ამავე სისტემაში მყოფი დამკვირვებელის თვალსაზრისით მასზე მოქმედებს ინერციის ცენტრიდანული ძალა

\(\vec{f}_{i}=m\omega ^{2}r\)

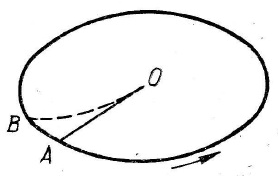
თუ მბრუნავ სისტემაში მყოფი სხეული მოძრაობს ამ სისტემის მიმართ გარკვეული სიჩქარით, მაშინ მასზე, გარდა ინერციის ცენტრიდანული ძალისა, მოქმედებს კიდევ ერთი ინერციის ძალა, რომელსაც კორიოლისის ძალა ეწოდება. ამ ძალის არსებობა შეიძლება აღმოვაჩინოთ მარტივი ცდით. განვიხილოთ ჰორიზონტალურ დისკო, რომელსაც შეუძლია ბრუნვა ვერტიკალური ღერძის ირგვლივ. გავაგოროთ ბირთვი დისკოს ცენტრისკენ, თუ დისკო არ ბრუნავს, მაშინ ბირთვი გაყვება OA-ს, მაგრამ თუ დისკოს ვაბრუნებთ (ნახ. 7) ნახაზე ნაჩვენები მიმართულებით, მაშინ ბირთვი გაჰყვება OB წირს, ამასთან მისი სიჩქარე დისკოს მიმართ შეიცვლის მიმართულებას. გამოდის რომ მბრუნავი დისკოს მიმართ ბირთვი მოძრაობს ისე, თითქოს მასზე მოქმედებს ბირთვის სიჩქარის მართობული \(\vec{f}_{k}\)  ძალა,რომელსაც კორიოლისის ძალა ეწოდება.

            თუ OA-ს გასწვრივ დისკოზე გავაკეთებთ ღარს, მაშინ ამით ვაიძულებთ ბირთვს იმოძრაოს OA მიმართულებით, ვინაიდან ბირთვის მოძრაობის დროს ამ ღარის მარჯვენა წიბო იმოქმედებს მასზე გარკვეული \(\vec{f}_{R}\) ძალით, ამიტომ დისკოსთან დაკავშირებული დამკვირვებელი დაასკვნის, რომ ეს \(\vec{f}_{R}\) ძალა წონასწორდება ბირთვზე მოქმედი მეორე ძალით, რომელიც სწორედ კორიოლისის ძალას წარმოადგენს.

            განვიხილოთ m მასის მატერიალური წერტილი, რომელიც მოძრაობს დისკოს მიმართულებით \(\vec{v}\)სიჩქარით. დისკოს ბრუნვის კუთხის სიჩქარე აღვნიშნოთ \(\vec{\omega }\)-თი და გამოვთვალოთ კორიოლისის ძალის სიდიდე. რადგან წერტილი მოძრაობს რადიალურად, ამიტომ ცხადია, რომ დისკოს ბრუნვის გამო წერტილის სიჩქარე დისკოს მიმართ იცვლება როგორც სიდიდით, ისე მიმართულებით. განვიხილოთ ეს ცვლილებები ცალ-ცალკე.

            წერტილის \(\vec{v}\) სიჩქარის რადიალური მდგენელი დისკოს მიმართ უცვლელი რჩება სიდიდით და მხოლოდ მობრუნდება მის მიმართ \(\omega\) კუთხური სიჩქარით დისკოს ბრუნვის საწინააღმდეგო მიმართულებით. ეს განაპირობებს ნორმალურ აჩქარებას

\(a^{_{n}}=\frac{v^{2}}{r}=\frac{vr\omega }{r}=v\omega\)

რომელიც OA რადიუსის პერპენდიკულარულია. ესაა წერტილის აჩქარების პირველი მდგენელი, რომელიც წერტილის სიჩქარის მიმართულების ცვლილებას გამოსახავს.

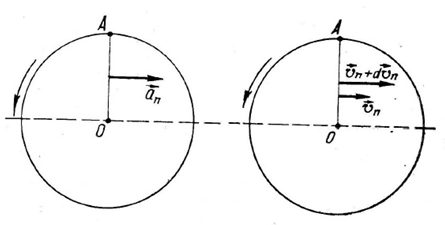
ვთქვათ dt დროში r იცვლება r-დან r+dr-მდე, სადაც dr = vdt. წერტილის სიჩქარის მდგენელი, რომელიც რადიუსის მართობული (\(v_{n}=\omega r\)), გაიზრდება dt დროში სიდიდით \(dv_{n}=\omega dr=\omega vdt\). სიჩქარის ამ ცვლილების შესაბამისი აჩქარება

\(a_{i}=\frac{\mathrm{d} v_{n}}{\mathrm{d} t}=\omega v\)

რაც აჩქარების მეორე მდგენელს წარმოადგენს და იგი სიჩქარის სიდიდის ცვლილებას გამოსახავს.

            გამოდის რომ აჩქარების ორივე მდგენელი ერთმანეთის ტოლია  და ერთნაირი მიმართულებისაა, რის გამოც სრული აჩქარება

\(a_{k}=2\omega v\)

ამ აჩქარებას კორიოლისის აჩქარება ეწოდება.

            მტკიცდება, რომ მიღებული ფორმულა მართებულია მბრუნავ დისკოზე წერტილის არა მარტო რადიალური, არამედ ნებისმიერი მიმართულებით მოძრაობის შემთხვევაში. თუკი წერტილის სიჩქარე \(\vec{v}\)ვექტორი ადგენს ბრუნვის ღერძთან \(\alpha\) კუთხეს, მაშინ კორიოლისის აჩქარება ტოლია

\(a_{k}=2\omega v\sin \alpha\)

ამასთან ყველა შემთხვევაში \(\vec{a}_{k}\) მართებულია \(\vec{v}\) და \(\vec{\omega }\) ვექტორებისა და მათთან ერთად ადგენს მარჯვენა სისტემას. ამის გამო კორიოლისის აჩქარების ვექტორი

\(\vec{a}_{k}=2\left [ \vec{v}\cdot \vec{\omega } \right ]\)

აქედან კორიოლისის ძალა

\(\vec{F}_{k}=2m\left [ \vec{v}\cdot \vec{\omega } \right ]\)

რადგან დედამიწა წარმოადგენს მბრუნავ სისტემას, ამიტომ კორიოლისის ძალის მოქმედებას ჩვენ ბევრ მოვლენაში ვხვდებით.