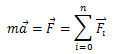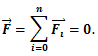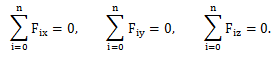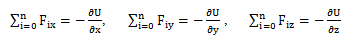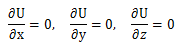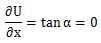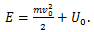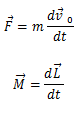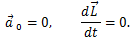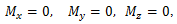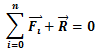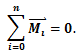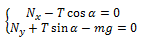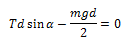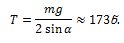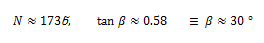მოამზადა: ელენე ფილიშვილმა

ხშირად ბუნებაში ვხვდებით ისეთ შემთხვევებს, როდესაც ურთიერთქმედების არსებობის მიუხედავად ნივთიერი წერტილი ან სხეული უძრავი რჩება.  ნივთიერი წერტილი წონასწორობაშია, თუ იგი, მოყვანილი უძრავ მდგომარეობაში, უძრავი რჩება შემდეგშიც.

ის პირობა, რომ ნივთიერი წერტილი უნდა იყოს უძრავ მდგომარეობაში ადვილი შესასრულებელია, რადგან დაკავშირებულია საყწისი პირობების შერჩევასთან. წონასწორობისთვის მნიშვნელოვანია მეორე პირობა, რომ ნაწილაკმა არ უნდა დაიწყოს მოძრაობა, ანუ მისი აჩქარება უნდა იყოს ნულის ტოლი 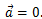 . მოძრაობის კანონების თანახმად  

სადაც   არის ნაწილაკზე მოქმედი ძალების ჯამი. რადგან წონასწორობაში

 მივიღებთ, რომ

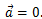
წონასწორობისთვის საჭიროა ნაწილაკზე მოქმედი ძალების ჯამი იყოს ნულის ტოლი. და პირიქით, თუ ნაწილაკზე მოქმედი ძალების ჯამი ნულის ტოლია, ნაწილაკი წონასწორობაშია.   ამ განტოლების ღერძებზე დაგეგმილებით მივიღებთ:

ე.ი. წონასწორობისთვის საჭიროა, რომ ნულის ტოლი იყოს ყოველ ღერძზე ძალების გეგმილების ჯამი.

წონასწორობის პირობები შეგვიძლია ჩავწეროთ პოტენციური ენერგიის გამოყენებითაც:

წონასწორობის შემთხვევაში შემდეგი პირობები უნდა სრულდებოდეს:

ე.ი. წონასწორობის მდებარეობაში პოტენციალური ენერგიის კოორდინატებით კერძო წარმოებულები ნულის ტოლი უნდა იყოს.

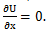
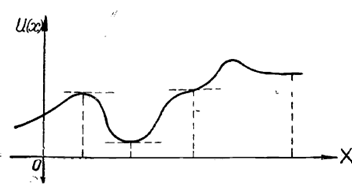
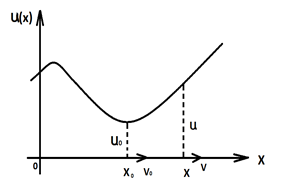
განვიხილოთ მარტივი შემთხვევა, როდესაც ნაწილაკი მოძრაობს მხოლოდ OX ღერძზე, მაშინ  გვექნება მხოლოდ      როგორც ცნობილია მათანალიზიდან, ფუნქციის წარმოებული თუ ნულის ტოლია რაიმე წერტილში მაშინ ფუნქციას აქვს ან ექსტრემუმი (მინიმუმი ან მაქსიმუმი) ან გადაღუნვის წერტილი ან ფუნქცია მუდმივია ამ წერტილის მახლობლობაში.

დავხაზოთ პოტენციური ენერგიის, როგორც x-ის ფუნქციის გრაფიკი, პოტენციალური მრუდი.

პოტენციალური მრუდი გვაძლევს არა მარტო პოტენციურ ენერგიას, არამედ წერტილზე მოქმედი ძალის მნიშვნელობასაც. ამისათვის საკმარისია აღებულ წერტილზე გავატაროთ მხები და გავზომოთ ამ მხებით შექმნილი კუთხე OX ღერძთან. ამ კუთხის ტანგესი მინუს ნიშნით გვაძლევს ნაწილაკზე მოქმედი ძალის მნიშვნელობას. წონასწორობაში

ე.ი. წონასწორობის სათანადო წერტილში მხები აბსცისთა ღერძის პარალელური უნდა იყოს. ნახაზი გვიჩვენებს, რომ ამას ადგილი აქვს მაქსიმუმის, მინიმუმის ან გადაღუნვის წერტილებში, ან ისეთ ნაწილში, სადაც მრუდი აბსცისთა ღერძის პარალელურია.

წონასწორობის მდებარეობიდან გამოყვანილი ნაწილაკის მოძრაობის ხასიათი განსხვავებული შეიძლება იყოს.

განვიხილოთ ჩაზნექილი ჭურჭლის ყველაზე დაბალ მდებარეობაში მოთავსებული ბირთვი, თუ მას წონასწორობის მდგომარეობიდან გამოვიყვანთ ის დაიწყებს რხევას წონასწორობის მდებარეობის მახლობლად. სხვანაირად იმოძრავებს ბირთვი, რომელიც ამოზნექილი ჭურჭლის ყველაზე მაღალ ადგილასაა მოთავსებული და გამოყვანილია წონასწორობის მდგომარეობიდან. ის კი არ დაუბრუნდება წონასწორობის ამ მდებარეობას, არამედ განაგრძობს დაშორებას ამ მდებარეობიდან. განვიხილოთ ისეთი შემთხვევა როდესაც ბირთვი წონასწორობაშია ბრტყელ ჰორიზონტულ ზედაპირზე. თუ გამოვიყვანთ ამ მდგომარეობიდან ის წონასწორობაში იქნება ახალ მდებარეობაშიც, რაც ნიშნავს, რომ ახალი მდებარეობაც წონასწორობის მდგომარეობას წარმოადგენს. 

 

 

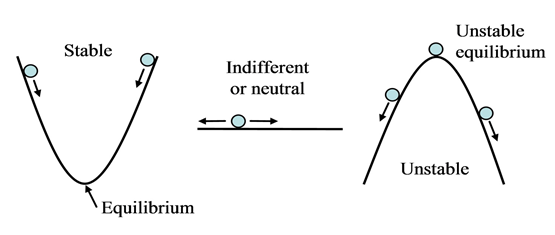
შეგვიძლია შემოვიღოთ წონასწორობის მდებარეობათა შემდეგი კლასიფიკაცია:

• მდგრადი წონასწორობა:  თუ წონასწორობიდან გამოყვანილი ნივთიერი წერტილი საკმაოდ მცირე ბიძგით ან გადახრით ისევ ამ მდგომარეობას უბრუნდება.
• არამდგრადი წონასწორობა:  როდესაც ნივთიერი წერტილი წონასწორობიდან გამოყვანის შემდეგ განაგრძობს ამ მდებარეობიდან დაშორებას.
• განურჩეველი წონასწორობა:  როდესაც წონასწორობის მახლობელი მდებარეობები ისევ წონასწორობის მდებარეობებს წარმოადგენენ.

 

დავაკავშიროთ წონასწორობის ეს სახეები პოტენციურ მრუდთან. ავღნიშნოთ x₀-ით მინიმუმის წერტილის შესაბამისი კოორდინატი, პოტენციური ენერგია ამ წერტილში იქნება 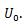.  ამ მდებარეობაში მყოფ ნაწილაკს მივანიჭოთ სიჩქარე v₀ და კინეტიკური ენერგია \(T_{0}=\frac{mv^{_{2}}}{2}\).   ნაწილაკის სრული ენერგია ბიძგის შემდეგ იქნება:

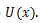
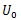
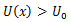
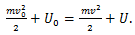
გარკვეული დროის შემდეგ ნაწილაკი გადავა ახალ მდებარეობაში კოორდინატით x და პოტენციური ენერგიით .  რადგან  პოტენციური ენერგიის მინიმალური მნიშვნელობაა, ცხადია,  რომ  .  მეორეს მხრივ, ენერგიის მუდმივობის კანონის თანახმად      .

აქედან მივიღებთ: 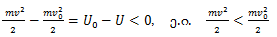, რაც იმას ნიშნავს, რომ ნაწილაკის კინეტიკური ენერგია შემცირდა, როდესაც იგი წონასწორობის მდებარეობიდან მეზობელ მდებარეობაში გადავიდა. მინიმალური პოტენციალური მდებარეობიდან გამოსული ნაწილაკი თანდათან ამცირებს თავის სიჩქარეს. დადგება მომენტი, როდესაც ნაწილაკი გაჩერდება და მასზე მოქმედი ძალების გავლენით დაბრუნდება საწყის მდგომარეობაში. ეს კი ნიშნავს, რომ მინიმალური პოტენციური ენერგიის მდებარეობას შეესაბამება მდგრადი წონასწორობა. ანალოგიურად შეიძლება დამტკიცდეს, რომ პოტენციალური ენერგიის მაქსიმუმს შეესაბამება არამდგრადი წონასწორობა. იმ შემთხვევაში, როდესაც პოტენციალური ენერგია უცვლელია ნაწილაკი გადახრის შემდეგ დარჩება იგივე მდგომარეობაში, რაც ნიშნავს, რომ ყველა მეზობელი მდებარეობა იქნება წონასწორობის მდებარეობა და გვექნება განურჩეველი წონასწორობა.

პოტენციური ენერგიის მრუდის გადაღუნვის წერტილში მხები აბსცისთა ღერძის პარალელურია, მაგრამ ამ წერტილის ერთ მხარეს პოტენციალური ენერგია მატულობს, მეორე მხარეს კი კლებულობს.

თუ წონასწორობის მდებარეობიდან ნაწილაკს გადავხრით იმ მხარეს, რომლის მიმართულებითაც პოტენციური ენერგია კლებულობს, ნაწილაკი სულ უფრო დაშორდება საწყის მდებარეობას. თუ ნაწილაკს გადავხრით პოტენციური ენერგიის ზრდის მიმართულებით, იგი თანდათან შეანელებს მოძრაობას, გაჩერდება და დაუბრუნდება საწყის მდებარეობას, გადასცდება და სულ უფრო და უფრო დაშორდება მას, ამ შემთხვევაშიც წონასწორობა იქნება არამდგრადი.

 

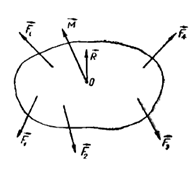
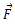
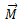
განვიხილოთ მყარი სხეულის შემთხვევა. მყარ სხეულზე მოქმედი ძალები შეგვიძლია დავიყვანოთ ერთ ძალაზე ან ერთ ძალთა წყვილზე. თუ მარეზულტირებელ ძალას და მომენტს ავღნიშნავთ სათანადოდ  და  -ით, მოძრაობის განტოლებები შემდეგი სახით ჩაიწერება:

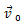
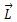
სადაც m არის მყარი სხეულის მასა,   - ინერციის ცენტრის სიჩქარე და  - იმპულსის მომენტი. გამოვიყენოთ წონასწორობის იგივე განსაზღვრა, რაც ნივთიერი წერტილის შემთხვევაში. თუ მყარი სხეული უძრავ მდგომარეობაშია და იგი არ გამოდის ამ მდებარეობიდან იგი წონასწორობაშია. ვინაიდან მყარ სხეულს შეუძლია შეასრულოს გადატანითი და ბრუნვითი მოძრაობა წონასწორობის მდებარეობაში არც ერთი მათგანი არ უნდა დაიწყოს. ეს იმას ნიშნავს, რომ ინერციის ცენტრის აჩქარება ნულის ტოლი უნდა იყოს და არ უნდა იცვლებოდეს იმპულსის მომენტი

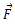
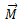
ამისთვის საჭიროა გარეშე ძალების  ჯამის და   ჯამის ნულთან ტოლობა

რაც წარმოადგენს წონასწორობის პირობას მყარი სხეულის შემთხვევაში. პირველი პირობა ისეთივეა, როგორც ნივთიერი წერტილის წონასწორობის პირობა და ამიტომ მის მიმართაც შეგვიძლია გავიმეოროთ ყველაფერი რაც ნივთიერი წერტილისთვის. შედარებით საინტერესო და მნიშვნელოვანია მეორე პირობა, რომელიც კრძალავს ბრუნვის დაწყებას. 

ვექტორული განტოლება შეგვიძლია დავშალოთ სამ სკალარულ განტოლებად, თუ დავაგეგმილებთ მას კოორდინატთა ღერძებზე. მივიღებთ

\(\vec{M}=0\)

რაც ნიშნავს, რომ საერთო მომენტის გეგმილები ღერძებზე ნულის ტოლი უნდა იყოს.

განვიხილოთ ზოგადი წონასწორობის პირობების ზოგიერთი კერძო შემთხვევა. ჩვეულებრივ პრაქტიკაში საჭიროა მყარი სხეულის წონასწორობის პირობების დადგენა იმ შემთხვევაში, როდესაც მყარი სხეული არ არის თავისუფალი, ე.ი. როდესაც მისი მოძრაობა შეზღუდულია გარეშე სხეულებით-ბმებით. ამ შემთხვევაში უშუალოდ მიღებულ ძალებს უნდა დაემატოს რეაქციის ძალები, ე.ი. ძალები, რომლებითაც გარეშე სხეულები მოქმედებენ განსახილველ სხეულზე.

 

განვიხილოთ მყარი სხეული, რომელსაც შეუძლია ბრუნვა უძრავი ღერძის ირგვლივ. ასეთ სხეულს ბერკეტი ეწოდება.

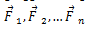
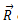
ვთქვათ, ბერკეტზე მოქმედებენ ღერძისადმი მართობულ სიბრტყეში მდებარე  ძალები. გარდა ამ ძალებისა, ბერკეტზე მოქმედებს კიდევ ღერძი რეაქციის  ძალით. წონასწორობის პირობის თანახმად, მოქმედი ძალების ჯამი უნდა იყოს ნულის ტოლი:

ეს  პირობა საშუალებას იძლევა ვიპოვოთ რეაქციის ძალა.

წონასწორობის მეორე პირობა - ძალთა მომენტების ჯამის ნულთან ტოლობა ჩაიწერება შემდეგნაირად:

 

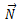
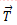
კედელზე ჩამოკიდებული სფერო:  ვერტიკალურ კედელზე  L სიგრძის თოკზე ჩამოკიდებულია m მასის სფერო, რომლის რადიუსია R.  იპოვეთ სფეროზე მოქმედი რეაქციის   და თოკის დაჭიმულობის  ძალები. ხახუნი კედელთან უგულებელყავით.

წონასწორობის პირობის თანახმად სფეროზე მოქმედ ძალთა ტოლქმედი ნულის ტოლია: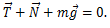    

 

ნახაზზე მოცემულ კოორდინატთა ღერძებზე  დაგემილებით მივიღებთ განტოლებათა შემდეგ სისტემას: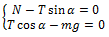 

როგორც ვხედავთ ეს ორი განტოლება საკმარისი არ არის საძიებელი ძალების გამოსათვლელად.  გვჭირდება კიდევ ერთი განტოლება. ამ განტოლებას წარმოადგენს წონასწორობის მეორე პირობა – მომენტების წესი. ავირჩიოთ რომელიმე ბრუნვის ღერძი. ამოცანის პირობიდან გამომდინარე ადვილი მისახვედრია, რომ მოხერხებულია ბრუნვის ღერძად ავირჩიოთ სფეროს ცენტრზე ნახაზის სიბრტყის მართობულად გამავალი ღერძი. ამ ღერძის მიმართ რეაქციის და სიმძიმის ძალების მომენტები ნულის ტოლია, რადგან მათი მოქმედების წრფე გადის ბრუნვის ღერძზე. 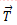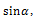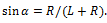მაშასადამე თოკის დაჭიმულობის  ძალის მოქმედების წრფეც უნდა გადიოდეს სფეროს ცენტრზე, წინააღმდეგ შემთხვევაში ეს ძალა გამოიწვევდა სფეროს ბრუნვას. ამრიგად თოკის დაჭიმულობის ძალაც რეაქციის და სიმძიმის ძალების მსგავსად სფეროს ზედაპირის მართობულად მოქმედებს. ეს საშუალებას გვაძლევს გამოვთვალოთ ,   კერძოდ .  განტოლებათა სისტემის ამოხსნით

მივიღებთ:

 

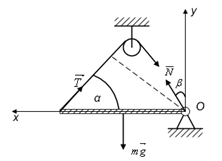
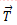
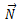
თოკით გაწონასწორებული ჰორიზონტული ღერო: m=30 კგ მასის ერთგვაროვანი ღერო,  რომელიც სახსრულად არის დამაგრებული  O წერტილში და რომელსაც შეუძლია ბრუნვა ხახუნის გარეშე, ჰორიზონტულად არის გაჩერებული ჭოჭონაქზე გადაკიდებული თოკით.  თოკი ღეროსთან ადგენს α=60◦C  კუთხეს. გამოთვალეთ თოკის დაჭიმულობის   და ღეროზე სახსარში მოქმედი რეაქციის  ძალები (ნახ. 2). ჩათვალეთ  g=10მ/წმ².

აქ უნდა მივიღოთ მხედველობაში, რომ სახსარში რეაქციის ძალა მიმართულია რაღაც β კუთხით ვერტიკალის მიმართ. მისი ერთი მდგენელი N_x მოქმედებს ღეროს გასწვრივხოლო მეორე N_y  მის მართობულად . მდგენელებით ვიპოვნით რეაქციის ძალის როგორც სიდიდეს, ასე მის მიმართულებას – β კუთხეს, კერძოდ

.

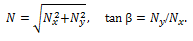
გამოვიყენოთ წონასწორობის პირობები. ღეროზე მოქმედი ძალებია რეაქციის, სიმძიმის და თოკის დაჭიმულობის ძალები. წონაწორობის პირობა გეგმილებში შემდეგნაირად ჩაიწერება:

ეს ორი განტოლება შეიცავს სამ უცნობს, მესამე განტოლების სახით გამოვიყენოთ მომენტების წესი. ბრუნვის ღერძად ავირჩიოთ სახსარზე ნახაზის სიბრტყის მართობულად გამავალი ღერძი.  მის მიმართ რეაქციის ძალის მომენტი ნულის ტოლია, დანარჩენი ორი ძალისთვის (რომლებიც სხეულს ანიჭებენ ურთიერთსაპირისპირო მაბრუნებელ ქმედებას) მომენტების წესი ასე გამოიყურება:

d  არის ღეროს სიგრძე. ამ განტოლებიდან მივიღებთ:

ამის შემდეგ პირველი ორი განტოლების ამოხსნა სირთულეს არ წარმოადგენს. საბოლოოდ მივიღებთ: