ძალის მომენტი რაიმე წერტილის მიმართ არის ამ წერტილიდან ძალის მოდების წერტილამდე გავლებული რადიუს ვექტორისა და ძალის ვექტორის ვექტორული ნამრავლი
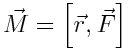 |
(1) |
ძალის მომენტის მოდული
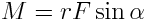 |
(2) |
ან სხვანაირად
| M=Fl | (3) |
სადაც l არის ძალის მხარი და წარმოადგენს უმოკლეს მანძილს ბრუნვის ღერძიდან ძალის მოქმედების წრფემდე.
ბრუნვის ღერძის მიმართ მატერიალური წერტილის ინერციის მომენტი არის
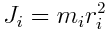 |
(4) |
სადაც mi არის მატერიალური წერტილის მასა, ხოლო ri არის მატერიალური წერტილის რადიუსი ბრუნვის ღერძიდან.
მყარი სხეულის ინერციის მომენტი მისი რომელიმე ღერძის მიმართ არის
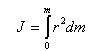 ან ან 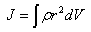 |
(5) |
სადაც ρ არის ნივთიერების სიმკვრივე; dV - ელემენტური მოცულობა. ინტეგრირებით შეიძლება მოიძებნოს მარტივი ფორმის სხეულების ღერძული ინერციის მომენტები, როცა ბრუნვის ღერძი მასათა ცენტრზე გადის.
| R რადიუსის სავსე ცილინდრი | 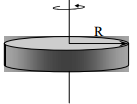 |
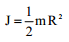 |
| R რადიუსის დისკო | 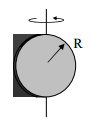 |
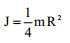 |
| R გარე რადიუსისა და r შიდა რადიუსის მქონე მილი | 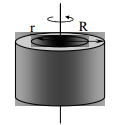 |
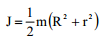 |
| R რადიუსის თხელკედლიანი ცილინდრი (მანჟეტი) | 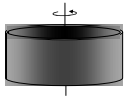 |
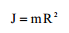 |
| R რადიუსის სავსე ბირთვი | 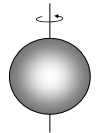 |
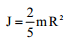 |
| R რადიუსის სფერული გარის (თხელი სფერული ფენა) | 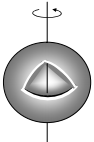 |
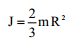 |
| l სიგრძის წვრილი ძელაკი | 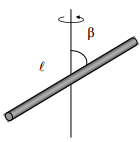 |
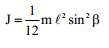 |
| სწორკუთხა პარალელეპიპედი | 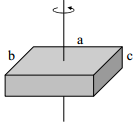 |
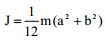 |
| კონუსი | 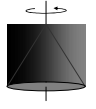 |
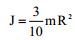 |
| პირამიდა | 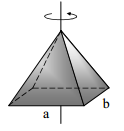 |
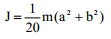 |
შტეინერის თეორემის თანახმად, სხეულის ინერციის მომენტი ნებისმიერი ღერძის მიმართ ტოლია ამ ღერძის პარალელური ღერძის მიმართ მისი ინერციის მომენტის ჯამისა სხეულის მასისსა და ამ ღერძებს შორის მანძილის კვადრატის ნამრავლთან:
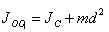 |
(6) |
სადაც m – სხეულის მასაა, d – ღერძებს შორის მანძილი.
მატერიალური წერტლის იმპულსის მომენტი რაიმე ღერძის მიმართ არის ამ ბრუნვის ღერძიდან ამ წერტილამდე გავლებული რადიუს-ვექტორის ვექტორული ნამრავლი იმპულსის ვექტორზე.
 |
(7) |
სხეულის იმპულსის მომენტი (მოძრაობის რაოდენობის მომენტი) რაიმე ღერძის მიმართ
 |
(8) |
ბრუნვითი მოძრაობის დინამიკის ძირითადი კანონი:
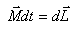 |
(9) |
სადაც M – სხეულზე მოდებული ძალების ჯამური მომენტია.
თუ J=const მაშინ
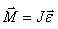 |
(10) |
მბრუნავი სხეულის უძრავი ღერძის მიმართ ბრუნვის კინეტიკური ენერგია
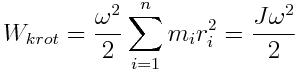 |
(11) |
სრული კინეტიკური ენერგია
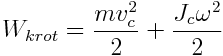 |
(12) |
სადაც vc მასათა ცენტრის გადატანითი მოძრაობის სიჩქარეა.
გარე ძალების მუშაობა მყარი სხეულის ბრუნვის დროს:
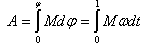 |
(5.13) |


