ვთქვათ K სისტემის x1 და x2 წერტილებში ერთდროულად მოხდა ორი ხდომილება დროის მომენტში t1=t2=t . ლორენცის გარდაქმნების თანახმად K’ სისტემაში ამ ხდომილებებს შეესატყვისება კოორდინატები
; 
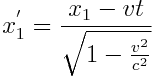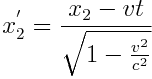
და დროის მომენტები
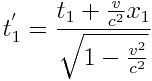; (1)
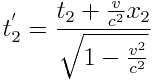(2)
დაწერილი ფორმულებიდან ჩანს, რომ თუ ხდომილებები K სისტემაში ხდება ერთსადაიმავე ადგილას ანუ (x1 = x2), მაშინ ისინი K’ სისტემაშიც დაემთხვევიან სივრცულად (x'1 = x'2) და დროშიც (t'1 = t'2).
თუკი K სისტემაში ხდომილებები სივრცეში აცდენილია (x1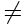 
x2), მაშინ K’ სისტემაშიც ისინი იქნება სივრცულად აცდენილი. მაგრამ (t'2 - t'1) სხვაობის ნიშანი განისაზღვრება v (x2 - x1) ნიშნით. აქედან გამომდინარეობს, რომ სხვადასხვა K’ სისტემაში (სხვადასხვა v-ს დროს) (t'2 - t'1) სხვაობას შეიძლება ჰქონდეს სხვადასხვა სიდიდე და სხვადასხვა ნიშანი. ეს ნიშნავს, რომ ზოგ სისტემაში ხდომილება 1 წინ გაუსწრებს ხდომილება 2-ს, ზოგში კი პირიქით. ნათქვამი ეხება მხოლოდ ხდომილებებს, რომელთა შორის არ არის მიზეზშედეგობრივი კავშირი.
მიზეზშედეგობრივად დაკავშირებული ხდომილებები (მაგალითად, გასროლა და ტყვიის სამიზნეში მოხვედრა) არცერთ სისტემაში არ იქნება ერთდროული და ყველგან მიზეზი წინ უსწრებს შედეგს. ამის საჩვენებლად გამოვიყენოთ (1) და (2) და ვწერთ
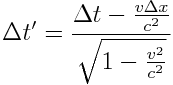
სადაც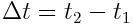 
, 
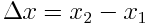ხოლო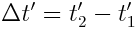 
ვთქვათ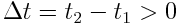 
ისე, რომ ხდომილება 1 წინ უსწრებს ხდომილება 2-ს. მაშინ ჩვენ შეგვიძლია ვიპოვნოთ ისეთი დამკვირვებელი K’ სისტემაში, ვისთვისაც ∆t' < 0. ამისთვის საჭიროა
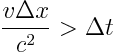
ანუ
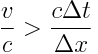
თუ 
, მაშინ ხდომილებათა თანმიმდევრობა შეიძლება შებრუნდეს მხოლოდ თუ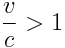 
, რაც შეუძლებელია. სხვა სიტყვებით რომ ვთქვათ თუ სინათლის სხივს აქვს საკმარისი დრო გადაფაროს მანძილი მეტი ვიდრე სივრცული დისტანციაა ხდომილებებს შორის, მაშინ ასეთი ხდომილებების თანმიმდევრობის შებრუნება შეუძლებელია. მეორეს მხრივ თუ 
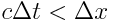, მაშინ თვით სინათლიუს სიჩქარესაც არ შეუძლია დააკავშიროს ეს ორი ხდომილება ამ დროში და რათქმაუნდა ვერცერთი სხვა საშუალება ვერ მოახერხებს ამას და ამ შემთხვევაში ვერავითარი მიზეზშედეგობრივი კავშირი ვერ გვექნება. ამ შემთხვევაში შეიძლება მოიძებნოს დამკვირვებელი, რომლისთვისაც 
პირობებშიც იქნება ხდომილებების თანმიმდევრობა შებრუნებული.