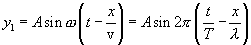
და არეკლილი ტალღის განტოლების
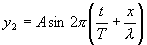
შეკრებით.
არეკლილი ტალღა მოძრაობს დაცემული ტალღის გავრცელების მიმართულების საპირისპირო მიმართულებით, ამიტომ х მანძილს ვიღებთ მინუს ნიშნით. ერთდროულად ორ რხევაში მონაწილე წერტილის წანაცვლება ტოლია ალგებრული ჯამისაა y=y1+y2. არართული გარდაქმნების შემდეგ მივიღებთ
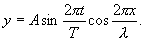 |
(8.15) |
ეს მდგარი ტალღის განტოლება განსაზღვრავს ტალღის ნებისმიერი წერტილის წანაცვლებას.
სიდიდე
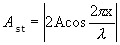 |
(8.16) |
არ არის დამოკიდებული დროზე და განსაზღვრავს х კოორდინატის მქონე ნებისმიერი წერტილის ამპლიტუდას. ყოველი წერტილი ასრულებს ჰარმონიულ რხევას Т პერიოდით. Аst ამპლიტუდა ყოველი წერტილისთვის სრულად არის განსაზღვრული, მაგრამ ტალღის ერთი წერტილიდან მეორეზე გადასვლისას იცვლება х-ის მიხედვით. თუ х-ს მივანიჭებთ მნიშვნელობებს 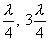 და ა.შ., მაშინ განტოლება (8.16)-ში ჩასმით მივიღებთ
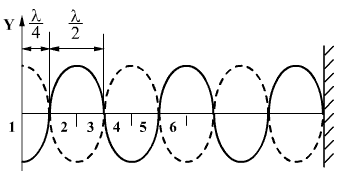
და ა.შ., მაშინ განტოლება (8.16)-ში ჩასმით მივიღებთ 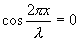 . შესაბამისად, ტალღის აღნიშნული წერტილები რჩება უძრავი, რადგან მათი რხევების ამპლიტუდები არის ნული. ამ წერტილებს ეწოდება მდგარი ტალღის კვანძები. წერტილებში, სადაც რხევებს აქვს მაქსიმალური ამპლიტუდა, ეწოდება ანტიკვანძები. მეზობელ კვანძებს ან მეზობელ ანტიკვანძებს შორის მანძილს ეწოდება მდგარი ტალღის სიგრძე და ტოლია
. შესაბამისად, ტალღის აღნიშნული წერტილები რჩება უძრავი, რადგან მათი რხევების ამპლიტუდები არის ნული. ამ წერტილებს ეწოდება მდგარი ტალღის კვანძები. წერტილებში, სადაც რხევებს აქვს მაქსიმალური ამპლიტუდა, ეწოდება ანტიკვანძები. მეზობელ კვანძებს ან მეზობელ ანტიკვანძებს შორის მანძილს ეწოდება მდგარი ტალღის სიგრძე და ტოლია
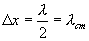
სადაც λ - მსრბოლი ტალღის სიგრძეა.
მდგარ ტალღაში მისი გავრცელების გარემოს ყველა წერტილი, რომელიც მოთავსებულია ორ მეზობელ კვანძს შორის, ირხევა ერთნაირ ფაზაში. გარემოს წერტილები, მოთავსებული კვანძის სხვადასხვა მხარეს, ირხევიან საპირისპირო ფაზებში, მათი ფაზები განსხვავდება \(\pi\)-ით ანუ კვანძზე გადასვლისას რხევის ფაზა ნახტომისებურად იცვლება \(\pi\)-ით. მსრბოლი ტალღებისგან განსხვავებით მდგარ ტალღაში ადგილი არ აქვს ენერგიის გადატანას იმის გამო, რომ მისი შემქმნელი პირდაპირი და უკუ ტალღაებს გადააქვთ ერთნაირი რაოდენობის ენერგია საპირისპირო მიმართულებით.

