ენერგიის ნაკადის სიმკვრივის ვექტორის რიცხვითი მნიშვნელობა განისაზღვრება შემდეგნაირად:

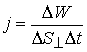(8.12)

სადაც 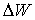 არის ენერგია, რომელიც  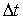 დროში ენერგიის გადატანის მიმართულების პერპენდიკულარულ  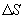ფართში გადააქვს ტალღას. სხვა სიტყვებით რომ ვთქვათ, ეს ვექტორი რიცხობრივად ტოლია სიმძლავრისა, რომელიც გადის გავრცელების პერპენდიკულარული ერთეულოვან ფართობში.  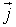ვექტორის მიმართულება ემთხვევა ტალღის ენერგიის გავრცელების მიმართულებას.

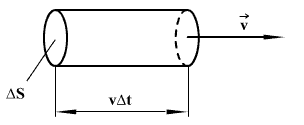
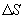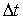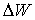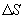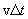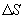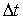 ფართში  დროში გავა  ენერგია, რომელიც მოთავსებულია  ფუძისა და  (ტალღის ფაზური სიჩქარეა) სიმაღლის ცილინდრში. თუ ცილინდრის ზომები საკმაოდ მცირეა ( და  სიმცირის გამო) იმისთვის რათა ცილინდრის ყველა წერტილში ენერგიის სიმკვრივე ჩაითვალოს ერთნაირად, მაშინ 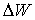შეიძლება მოიძებნოს როგორც w ენერგიის სიმკვრივისა და ცილინდრის მოცულობის ნამრავლი,

რაც ტოლია 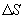v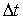 , მაშინ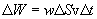 
ჩავსვათ ეს გამოსახულებები (8.12)-ში, მივირებთ

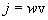
თუ განვიხილავთ v ფაზურ სიჩქარეს ვექტორად, რომელიც მიმართულია ტალღის გავრცელების (და ენერგიის გადატანის), შეიძლება დავწეროთ

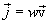(8.13)

ამ სიდიდეს უწოდებენ ენერგიის ნაკადის სიმკვრივის ვექტორს.

ენერგიის ნაკადის სიმკვრივის ვექტორი, ისევე როგორც ენერგიის სიმკვრივე განსხვავებულია სივრცის სხვადასხვა წერტილში. მისი დროითი საშუალო ტოლია:

\(\fn_jvn \vec{j}_{m}=\vec{w}\vec{v}=\frac{1}{2}\rho A^{2}\omega ^{2}\vec{v}\)