ვიპოვნოთ დრეკადი გარემოს dV მცირე მოცულობის ენერგიის ცვლილება, დაკავშირებული გარემოში ბრტყელი ტალღის გავრცელებასთან, რომელიც მოცემულია განტოლებით

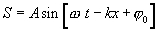(8.9)

dV მოცულობის სიმცირის გამო შეიძლება ჩავთვალოთ, რომ მასში მოქცეული ყველა ნაწილაკი ირხევა ერთ ფაზაში, ასე რომ მათი სიჩქარეები ერთნაირია და ტოლია

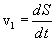
ამიტომ dV მოცულობის გარემოს კინეტიკური ენერგია, რომელიც დაკავშირებულია რხევით მოძრაობებთან, ტოლია

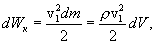
სადაც ρ გარემოს სიმკვრივეა. (8.9)-დან გამოდის
\(V_{1}=A\omega \cos \left [ \omega t-kx+\varphi _{0} \right ]\)
ამიტომ

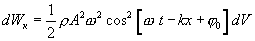(8.10)

ტალღური მოძრაობისას dV მოცულობის დეფორმაციის (განივი ტალღის შემთხვევაში წანაცვლების დეფორმაცია, ხოლო გასწვრივი ტალღის შემთხვევაში მოცულობითი შეკუმშვა) მუშაობის გამოთვლა აჩვენებს, რომ dV მოცულობის გარემოს პოტენციური ენერგია  dW_p ტოლია მისი კინეტიკური ენერგიისა. დრეკადი გარემოს dV ელემენტარული მოცულობის რხევითი მოძრაობის სრული მექანიკური ენერგია ტოლია მისი კინეტიკური და პოტენციური ენერგიების ჯამისა.

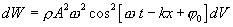(8.11)