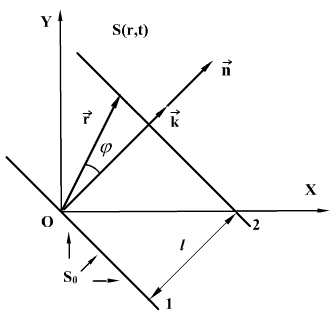
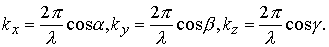მივიღოთ განტოლება ბრტყელი ტალღისა, რომელიც ვრცელდება მიმართულებით, რაც х, у, z ღერძებთან ადგენს კუთხეებს α, β, γ. კოორდინატთა სათავეზე გამავალ სიბრტყეში რხევებს ჰქონდეს სახე  .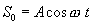

ავიღოთ ტალღური ზედაპირი (სიბრტყე), რომელიც კოორდინატთა სათავისგან დაშორებულია l-ით. ამ სიბრტყეში რხევები О წერტილში რხევისგან ჩამორჩება 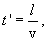  დროით, მაშინ ტალღის განტოლება

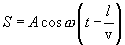(8.4)

გამოვსახოთ l დაშორება განსახილველი ზედაპირის წერტილების 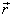 რადიუს-ვექტორით. ამისთვის შემოვიტანოთ ერთეულოვანი ვექტორი 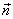, რომელიც ტალური ზედაპირის ნორმალს წარმოადგენს. სკალარული ნამრავლი

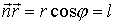
ჩავსვათ l-ის მნიშვნელობა (8.4) განტოლებაში და ომეგა შევიტანოთ ფრჩხილებში

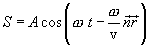
ფარდობა  ტოლია k ტალღური რიცხვისა. ვექტორს 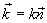, რომელიც მოდულით ტოლია ტალღური რიცხვისა  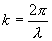და მიმართულია ტალღური ზედაპირის ნორმალის გასწვრივ, ეწოდება ტალღური ვექტორი.  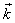ვექტორის შემოღებით მივიღებთ

.

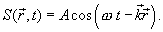(8.5)

რათა გადავიდეთ წერტილის რადიუს-ვექტორიდან მის კოორდინატებზე х, у, z , გამოვსახოთ სკალარული ნამრავლი 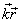 საკოორდინატო ღერძებზე ვექტორების პროექციებით :

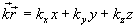
მაშინ ბრტყელი ტალღის განტოლება მიიღებს სახეს:

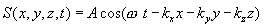(8.6)

სადაც