საერთო წრფის გასწვრივ მიმართული ჰარმონიული რხევების შეკრება.

განვიხილოთ ერთპერიოდიანი ერთნაირი მიმართულების რხევები, რომელთაც აქვთ განსხვავებული საწყისი ფაზები და ამპლიტუდები. შესაკრები რხევების განტოლებები მოცემულია შემდი სახით:

,

,

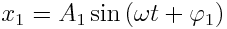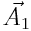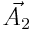სადაც x₁ და x₂ - წანაცვლებებია; A₁ და A₂ - ამპლიტუდები; ϕ₁ და ϕ₂ - შესაკრები რხევების საწყისი ფაზები. ჯამური რხევის ამპლიტუდის განსაზღვრა მოსახერხებელია ვექტორული დიაგრამით, რომელზეც გადაზომილია  და  ამპლიტუდების ვექტორები х-ისადმი ϕ₁ და ϕ₂ კუთხეებით და პარალელოგრამის წესით მიღებულია ჯამური რხევის ამპლიტუდა 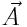. თუ თანაბრად ვაბრუნებთ ვექტორთა სისტემას (პარალელოგრამს) და ვექტორებს დავაგეგმილებთ OY ღერძზე, მაშინ მათი მდგენელები შეასრულებენ ჰარმონიულ რხევებს მოცემული განტოლებების შესაბამისად.  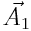 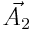და  ვექტორების ურთიერთგანლაგება, ამასთან, არ იცვლება, ამიტომ ჯამური  ვექტორის პროექციის  რხევაც იქნება ჰარმონიული.

აქედან ვასკვნით, რომ ჯამური მოძრაობა არის ჰარმონიული რხევა, რომელსაც აქვს განსაზღვრული ციკლური სიხშირე. განვსაზღვროთ ჯამური რხევის. სამკუთხედში ΔOK₁K კუთხე OK₁K=[π-(ϕ₂-ϕ₁)] (პარალელოგრამის მოპირისპირე კუთხეების ტოლობიდან გამომდინარე).

შესაბამისად

2(ϕ₂-ϕ₁)+2α=2π

აქედან

α=[π-(ϕ₂-ϕ₁)]

კოსინუსების თეორემის თანახმად

A²=A₁²+A₂²-2A₁A₂cos[π-(ϕ₂-ϕ₁)]

ანუ

A2=A12+A22-2A1A2cos(ϕ2-ϕ1)

(7.12)

ჯამური რხევის საწყისი ფაზა ϕ₀ განისაზღვრება ΔOKD-დან :

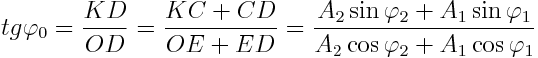
თანაფარდობები ფაზისა და ამპლიტუდისთვის საშუალებას გვაძლევს მოვძებნოთ ჯამური მოძრაობის ამპლიტუდა და საწყისი ფაზა და შევადგინოთ მისი განტოლება

x=Asin(ωt+ϕ)

 

ფეთქვა

განვიხილოთ შემთხვევა, როცა ორი შესაკრები რხევის სიხშირეები განსხვავდებიან ერთმანეთისგან სიდიდით ω₂-ω₁=Δω, და ვთქვათ მათი ამპლიტუდები ერთნაირია ხოლო საწყისი ფაზები ϕ₀=0 , ანუ x₁=Asin(ω₁t), x₂=Asin(ω₂t). შევკრიბოთ ეს განტოლებები ანალიზურად

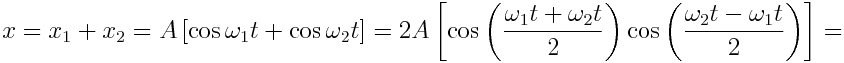
გარდავქმნათ

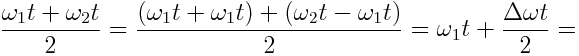
მაშინ

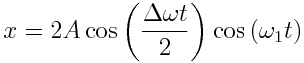
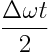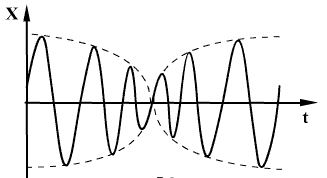
რადგან  მაინც ნელა იცვლება, სიდიდეს 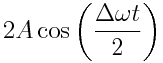 ვერ ვუწოდებთ ამპლიტუდას ამ სიტყვის სრული გაგებით (ამპლიტუდა მუდმივი სიდიდეა). პირობითად ამ სიდიდეს შეიძლება ვუწოდოთ ცვლადი ამპლიტუდა. ასეთი რხევების გრაიკი მოცემულია ნახაზზე. შესაკრებ რხევებს აქვთ ერთნაირი ამპლიტუდები, მაგრამ განსხვავებული პერიოდები, ამასთან T₁ da T₂ მცირედ განსხვავდება ერთმანეთისგან. ასეთი რხევების შეკრებისას დაიმზირება ფეთქვა. წამში ფეთქვათ n რიცხვი განისაზღვრება შესაკრები რხევების სიხშირეთა სხვაობით, ანუ

n=ν₁-ν₂

ფეთქვას შეიძლება დავაკვირდეთ ორი კამერტონის ჟღერისას, როცა მათი სიხშირეები ახლოს არის ერთმანეთთან.

ურთიერთმართობი რხევების შეკრება.

ვთქვათ მატერიალური წერტილი ერთდროულად მონაწილეობას ორ ჰარმონიულ რხევაში, რომლებიც ერთნაირი Т პერიოდით მიმდინარეობს ორ ურთიერთმართობი მიმართულებით. ამ მიმართულებებს მივაბათ მართკუთხა XOY კოორდინატთა სისტემა, ისე, რომ კოორდინატთა სათავე მოვათავსოთ მატერიალური წერტილის წონასწორობის მდგომარეობის მდებარეობაში. ОХ და OY ღერძების მიმართ წერტილის წანაცვლებები აღვნიშნოთ, შესაბამისად, х-ით და у-ით.

განვიხილოთ რამდენიმე კერძო შემთხვევა.

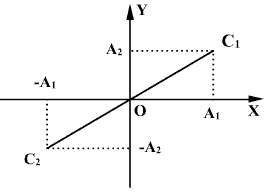
ა. რხევების საწყისი ფაზები ტოლია. ავირჩიოთ დროის ათვლის საწყისი ისე, რომ საწყისი ორივე რხევის საწისი ფაზები იყოს ნული. მაშინ წანაცვლებები ОХ და OY ღერძების გასწვრივ გამოისახება შემდეგი განტოლებებით:

x=A₁sin(ωt), y=A₂sin(ωt)

შევაფარდოთ ამ განტოლებების მხარეები და მივიღებთ С წერტილის ტრაექტორიის განტოლებას:

  ანუ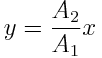  

შესაბამისად, ორი ურთიერთმართობი რხევის შეკრების შედეგად წერტილი  С ირხევა  С₁С₂  წრფის გასწვრივ, რომელიც კოორდინატთა სათავეზე გადის.

ბ. ფაზათა საწყისი სხვაობა ტოლია π ამ შემთხვევაში რხევისს განტოლებას აქვს სახე:

x=A₁sin(ωt+π)=-A₁sin(ωt), y=A₂sin(ωt)

წერტლის ტრაექტორიის განტოლებაა

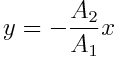(7.15)

შესაბამისად, წერტილი С ირხევა С₁С₂ მონაკვეთის გასწვრივ, იმ წრფისა, რომელიც გადის კოორდინატთა სათავეზე, მაგრამ იმყოფება პირველი შემთხვევისგან განსხვავებულ კვანდრანტებში. ჯამური რხევის А ამპლიტუდა ორივე განხილულ შემთხვევაში ტოლია

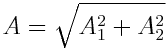
გ. ფაზათა საწყისი სხვაობა ტოლია  .

რხევის განტოლებას აქვს სახე:

,   

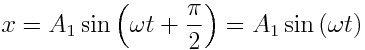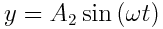
გავყოთ პირველი განტოლება A₁-ზე , მეორე - A₂-ზე :

,   

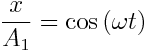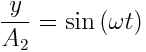
ორივე ტოლობა ავიყვანოთ კვადრატში და შევკრიბოთ. მივიღებთ მერხევი წერტილის მოძრაობის ტრაექტორიის შემდეგ განტოლებას

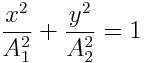(7.16)

С მერხევი წერტილი მოძრაობს ელიფსზე, რომლის ნახევარღერძებია A₁ და A₂. ტოლი ამპლიტუდების დროს A₁=A₂=A ჯამური მოძრაობის ტრაექტორია იქნება წრეწირი x²+y²=A². ზოგად შემთხვევაში, როცა ω₁≠ω₂, მაგრამ ჯერადია, ანუ ω₁=kω₂, ურთიერთპერპენდიკულარული რხევების შეკრებისა წერტილი მოძრაობს მრუდებზე, რომლებსაც ლისაჟუს მრუდები ეწოდება. ამ მრუდების კონფიგურაცია დამოკიდებულია შემადგენელი რხევების ამპლიტუდების, საწყისი ფაზებისა და პერიოდების თანაფარდობებზე.