ვთქვათ K’ სისტემის მიმართ უძრავ х’ წერტილში ხდება 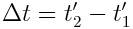 ხანგრძლივობის მოვლენა. მოვლენის სწყისს ამ სისტემაში შეესაბამება x'1=х’ წერტილი და t'1 დროის მომენტი, დასასრულს კი x'2=х’ წერტილი და t'2 დროის მომენტი. K სისტემის მიმართ წერტილი, რომელშიც ხდება მოვლენა, გადაადგილდება. ლორენცის გარდაქმნის თანახმად:
ხანგრძლივობის მოვლენა. მოვლენის სწყისს ამ სისტემაში შეესაბამება x'1=х’ წერტილი და t'1 დროის მომენტი, დასასრულს კი x'2=х’ წერტილი და t'2 დროის მომენტი. K სისტემის მიმართ წერტილი, რომელშიც ხდება მოვლენა, გადაადგილდება. ლორენცის გარდაქმნის თანახმად:
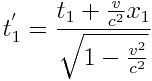 ;
; 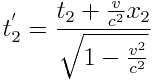
აქედან
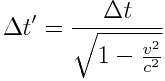
ანუ
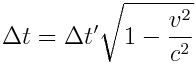
სხეულთან ერთად მოძრავი საათით ათვლილ \(\Delta t\) დროს უწოდებენ სხეულის საკუთარ დროს. როგორც ჩანს საკუთარი დრო ყოველთვის ნაკლებია, ვიდრე დრო, რომელიც აითვლება სხეულის მიმართ მოძრავი საათით. დროის შენელების რელატივისტური ეფექტი პრინციპში შესაძლებელს ხდის "მომავალში მოგზაურობას" (და არა წარსულში). მართლაც, ვთქვათ კოსმოსური ხომალდი, რომელიც მოძრაობს 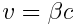 სიჩქარით (სადაც
სიჩქარით (სადაც 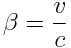 ) დედამიწის მიმართ, გდაფრინდა დედამიწიდან რომელიმე ვარსკვლავზე და გადმოფრინდა უკან. თუ სინათლე სინათლის სხივი ვარსკვლავიდან დედამიწამდე
) დედამიწის მიმართ, გდაფრინდა დედამიწიდან რომელიმე ვარსკვლავზე და გადმოფრინდა უკან. თუ სინათლე სინათლის სხივი ვარსკვლავიდან დედამიწამდე 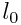 მანძილს გადის
მანძილს გადის 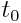 დროში, მაშინ
დროში, მაშინ 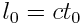 დედამიწის დამკვირვებლისთვის ფრენის ხანგრძლივობა იქნება:
დედამიწის დამკვირვებლისთვის ფრენის ხანგრძლივობა იქნება:
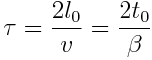
სწორედ ამდენით დაბერდებიან ადამიანები დედამიწაზე ხომალდის დაბრუნების მომენტისთვის. მეორეს მხრივ, კოსმოსურ ხომალდზე დაყენებული საათის მიხედვით, ფრენას დასჭირდება ნაკლები დრო, რომელიც ტოლია:

ფარდობითობის პრინციპიდან გამომდინარე ხომალდზე ყველა პროცესი (მათ შორის კოსმონავტების დაბერების პროცესიც) მიდის ზუსტად ისე, როგორც დედამიწაზე, მაგრამ არა დედამიწის საათით, არამედ ხომალდზე მდებარე საათით. ვთქვათ, მაგალითად 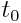 =500წელს და
=500წელს და 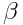 =0,9999. მაშინ
=0,9999. მაშინ 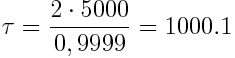 წელი, ხოლო
წელი, ხოლო 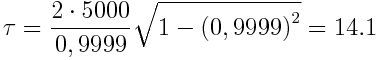 წელი
წელი


