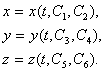კლასიკურ ფიზიკაში, როგორც უკვე ვაჩვენეთ, მატერიალური წერტილის მდგომარეობა სრულად განისაზღვრება მისი კოორდინატებით х, у, z. და სიჩქარის კომპონენტებით 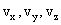 დროის მოცემულ მომენტში, ანუ  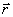რადიუს ვექტორით და მისი სიჩქარით. მითითებული ფუნქციონალური დამოკიდებულებების გათვალისწინებით ნიუტონის მეორე კანონს აქვს სახე:

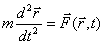(3.14)

თუ ჩავთვლით, რომ ცნობილია რეზულტატური ძალა 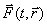 როგორც კოორდინატებისა და დროის ფუნქცია, მაშინ განტოლება (3.14) წარმოადგენს მეორე რიგის დიფერენციალურ განტოლებას მატერიალური წერტილის  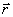რადიუს-ვექტორის მიმართ.

თუ ამოვხსნით (3.14) განტოლებას მოცემული მარჯვენა ნაწილით, შეიძლება განვსაზღვროთ სხეულის რადიუს-ვექტორი დროის ნებისმიერ მომენტში და ამით სხეულის მოძრაობის ტრაექტორია დავადგინოთ. ამასთან, მოძრაობის დამოუკიდებლობისგან გამომდინარე, რთულ ვექტორულ განტოლებას (3.14), რომელიც ზოგადად აღწერს  სხეულის მრუდწირულ მოძრაობას, ცვლიან მისი ექვივალენტური სამი განტოლების სისტემით, თითოეული მათგანი აღწერს წრფივ მოძრაობას შესაბამისი х, у და z ღერძის გასწვრივ.

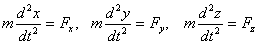(3.15)

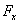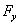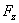სადაც ,  და  არის 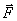 ვექტორის პროექციები კოორდინატთა ღერძებზე. х, у და z  კოორდინატებს განსაზღვრავენ (3.15) განტოლების ორმაგი ინტეგრირებით. ყოველი ინტეგრირებისას წარმოიშვება განუსაზღვრელი მუდმივები. ამიტომ მოძრაობის კანონის ცალსახად გამოყოფისთვის აუცილებელია მოძრაობის განტოლებას დაემატოს ორი პირობა, რომელიც განსაზღვრავს ამ მუდმივებს. ამ პირობებს აფიქსირებენ, მატერიალური წერტილის მდგომარეობის მოცემით რაღაც მომენტში (ჩვეულებრივ საწყის მომენტში), ანუ მიუთითებენ რადიუს-ვექტორის  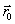მნიშვნელობას ან კოორდინატების  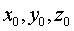მნიშვნელობებს და სიჩქარის  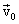მნიშვნელობას საწყის t=0 მომენტში. ასეთნაირად, (3.15)-ის ინტეგრირების შედეგად ვღებულობთ х, у, z კოორდინატებს, როგორც დროისა და ინტეგრირების ორი  მუდმივის ფუნქციებს: