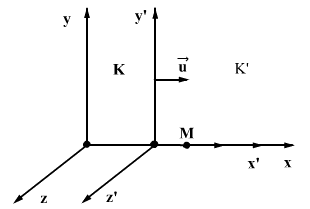
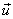 სიჩქარით მოძრავი (K’). М სხეულის კოორდინატები К სისტემაში იყოს x:y:z , ხოლო К’-ში - x’:y’:z’. ეს კოორდინატები ერთმანეთს უკავშირდებიან თანაფარდობებით, რომელთაც ეწოდებათ გალილეის გარდაქმნები
სიჩქარით მოძრავი (K’). М სხეულის კოორდინატები К სისტემაში იყოს x:y:z , ხოლო К’-ში - x’:y’:z’. ეს კოორდინატები ერთმანეთს უკავშირდებიან თანაფარდობებით, რომელთაც ეწოდებათ გალილეის გარდაქმნები
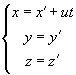
გავაწარმოოთ ეს განტოლებები დროით და გავითვალისწინოთ, რომ 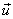 =const, ვიპოვნით თანაფარდობებს სიჩქარეებსა და აჩქარებებს შორის:
=const, ვიპოვნით თანაფარდობებს სიჩქარეებსა და აჩქარებებს შორის:
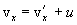 |
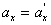 |
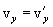 |
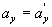 |
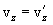 |
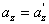 |
ამდენად, თუ К სისტემაში სხეულს აქვს а აჩქარება, მაშინ ასეთივე აჩქარება ექნება მას К’ სისტემაშიც.
ნიუტონის მეორე კანონის თანახმად:
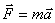
ანუ ნიუტონის მეორე კანონი ორივე სისტემაში ერთნაირია.
როცა 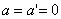 გვაქვს ინერციით მოძრაობა, ამდენად სამართლიანია ნიუტონის პირველი კანონიც, ანუ ჩვენს მიერ განხილული მოძრავი სისტემა არის ინერციული. შესაბამისად, ნიუტონის განტოლებები მატერიალური წერტილისთვის, ასევე მატერიალური წერტილების ნებისმიერი სისტემისთვის ერთნაირია ყველა ინერციულ ათვლის სისტემაში - ინვარიანტულია გალილეის გარდაქმნების მიმართ. ამ შედეგს ეწოდება ფარდობითობის მექანიკური პრინციპი (გალილეის ფარდობითობის პრინციპი) და ფორმულირდება შემდეგნაირად: ჩაკეტილი სისტემის წრფივი და თანაბარი მოძრაობა (რომელიმე ათვლის სისტემის მიმართ) არ მოქმედებს მასში მექანიკური პროცესების მიმდინარეობის კანონზომიერებებზე. შესაბამისად, მექანიკაში ყველა ინერციული სისტემა თანაბარია. ამიტომ თვით სისტემის შიგნით ვერავითარი მექანიკური ცდით ვერ დავადგენთ მოძრაობს სისტემა წრფივად და თანაბრად თუ უძრავია.
გვაქვს ინერციით მოძრაობა, ამდენად სამართლიანია ნიუტონის პირველი კანონიც, ანუ ჩვენს მიერ განხილული მოძრავი სისტემა არის ინერციული. შესაბამისად, ნიუტონის განტოლებები მატერიალური წერტილისთვის, ასევე მატერიალური წერტილების ნებისმიერი სისტემისთვის ერთნაირია ყველა ინერციულ ათვლის სისტემაში - ინვარიანტულია გალილეის გარდაქმნების მიმართ. ამ შედეგს ეწოდება ფარდობითობის მექანიკური პრინციპი (გალილეის ფარდობითობის პრინციპი) და ფორმულირდება შემდეგნაირად: ჩაკეტილი სისტემის წრფივი და თანაბარი მოძრაობა (რომელიმე ათვლის სისტემის მიმართ) არ მოქმედებს მასში მექანიკური პროცესების მიმდინარეობის კანონზომიერებებზე. შესაბამისად, მექანიკაში ყველა ინერციული სისტემა თანაბარია. ამიტომ თვით სისტემის შიგნით ვერავითარი მექანიკური ცდით ვერ დავადგენთ მოძრაობს სისტემა წრფივად და თანაბრად თუ უძრავია.


