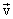 სიჩქარე ვერ ჩაითვლება მთელი სხე ულის მახასიათებლად.
სიჩქარე ვერ ჩაითვლება მთელი სხე ულის მახასიათებლად.
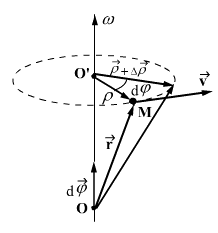
ვთქვათ წერტილი О არის სხეულის ბრუნვის ცენტრი, ხოლო ОО' არის ბრუნვის უძრავი (ან მყისიერი) ღერძი.
ნებისმიერი М წერტილის მდებარეობა მოიცემა О ცენტრიდან გავლებული 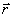 რადიუს-ვექტორის მეშვეობით. ნახაზიდან ჩანს, რომ:
რადიუს-ვექტორის მეშვეობით. ნახაზიდან ჩანს, რომ:
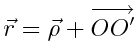 ,
,
სადაც 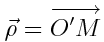 არის რადიუს-ვექტორი, გავლებული იმ წრეწირის ცენტრამდე, რომელზეც მოძრაობს М წერტილი. მცირე დროში
არის რადიუს-ვექტორი, გავლებული იმ წრეწირის ცენტრამდე, რომელზეც მოძრაობს М წერტილი. მცირე დროში 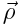 ვექტორი შემობრუნდება ОО' ღერძის პერპენდიკულარულ სიბრტყეში მცირე
ვექტორი შემობრუნდება ОО' ღერძის პერპენდიკულარულ სიბრტყეში მცირე 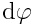 კუთხით. იგივე კუთხით შემობრუნდება
კუთხით. იგივე კუთხით შემობრუნდება 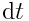 დროში სხეულის ნებისმიერი სხვა წერტილი, რადგან წინააღმდეგ შემთხვევაში მანძილები ამ წერტილებს შორის უნდა შეცვლილიყო. ამდაგვარად, შემობრუნების კუთხე ახასიათებს მთელ მბრუნავ სხეულს დროის მცირე შუალედში. მოსახერხებელია შემოვიღოთ სხეულის ელემენტარული (მცირე) შემობრუნების
დროში სხეულის ნებისმიერი სხვა წერტილი, რადგან წინააღმდეგ შემთხვევაში მანძილები ამ წერტილებს შორის უნდა შეცვლილიყო. ამდაგვარად, შემობრუნების კუთხე ახასიათებს მთელ მბრუნავ სხეულს დროის მცირე შუალედში. მოსახერხებელია შემოვიღოთ სხეულის ელემენტარული (მცირე) შემობრუნების 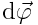 ვექტორი, რომელიც რიცხობრივად უდრის
ვექტორი, რომელიც რიცხობრივად უდრის 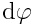 -ს და მიმართულია მყისიერი ღერძის გასწვრივ ისე, რომ მისი ბოლოდან სხეულის ბრუნვა საათის ისრის საწინააღმდეგოდ გამოჩნდეს.
-ს და მიმართულია მყისიერი ღერძის გასწვრივ ისე, რომ მისი ბოლოდან სხეულის ბრუნვა საათის ისრის საწინააღმდეგოდ გამოჩნდეს.


