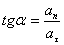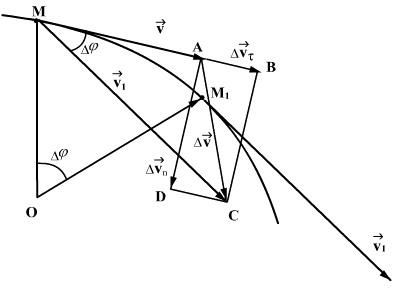
წრფივი მოძრაობისას სიჩქარისა და აჩქარების ვექტორები ემთხვევა ტრაექტორიის მიმართულებას. განვიხილოთ მატერიალური წერტილის ბრტყელი მრუდწირული მოძრაობა. ტრაექტორიის ნებისმიერ წერტილში სიჩქარის ვექტორი მიმართულია ტრაექტორიის მხების გასწვრივ. დავუშვათ, რომ ტრაექტორიის М წერტილში სიჩქარე იყო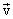 
, ხოლო.М1 წერტილში გახდა 
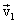. ამასთან ვთვლით, რომ М წერტ М1 წერტლიში გადასვლის დროის მონაკვეაათი იმდენად მცირეა, რომ აჩქარების სიდიდისა და მიმართულების ცვლილება შეიძლება უგულებელვყოთ. იმისათვის რათა მოვძებნოთ 
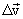სიჩქარის ცვლილება, აუცილებელია განვსაზღვროთ ვექტორული სხვაობა:
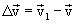
ამისათვის გადავიტანოთ 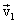თავის თავის პარალელურად ისე, რომ მისი სათავე დავამთხვიოთ М წერტილს. ორი ვექტორის სხვაობა ტოლია 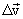ვექტორისა, რომელიც აერთებს მათ ბოლოებს და ტოლია სიჩქარეებზე როგორც გვერდებზე აგებული МАС სამკუთხედის АС გვერდისა. დავშალოთ 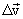ვექტორი ორ მდგენელად АВ АD, და აღვნიშნოთ ისინი შესაბამისად 
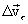და 
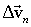. ამდაგვარად სიჩქარის ცვლილების ვექტორი 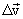ტოლია ორი ვექტორის ვექტორული ჯამისა:
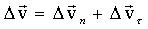
განსაზღვრების თანახმად:
 |
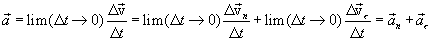(1.15) |
ტანგენციური აჩქარება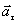 
ახასიათებს მოძრაობის სიჩქარის რიცხვითი მნიშვნელობის ცვლილების სისწრაფეს და მიმართულია ტრაექტორიის მხების გასწვრივ.
შესაბამისად
 |
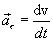(1.16) |
ნორმალური აჩქარება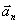 
ახასიათებს სიჩქარის მიმართულების ცვლილების სისწრაფეს. გამოვთვალოთ ვექტორი:
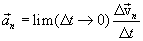
ამისთვის М და М1 წერტილებში ტრაექტორიის მხებების მიმართ გავავლოთ პერპენდიკულარები. გადაკვეთის წერტილი აღვნიშნოთ О-თი. საკმაოდ მცირე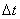 
-სთვის მრუდწირული ტრაექტორიის უბანი R რადიუსიანი წრეწირის ნაწილად შეიძლება ჩაითვალოს. სამკუთხედები МОМ1 და МВС მსგავსებია, რადგან წარმოადგენენ ტოლფერდა სამკუთხედებს, რომელთაც წვერის კუთხეები ტოლი აქვთ. ამიტომ:
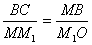
ანუ
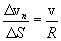
მაგრამ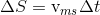 
, მაშინ:
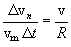
გადავიდეთ ზღვარზე როცა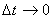 
და გავითვალისწინოთ, რომ ამ დროს vm=v, ვიპოვით:
,
 |
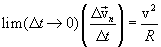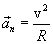(1.17) |
რადგან როცა 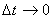მაშინ კუთხე 
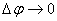, ამ აჩქარების მიმართულება ემთხვევა 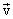სიჩქარის ნორმალის მიმართულებას, ანუ აჩქარების ვექტორი 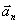პერპენდიკულარულია სიჩქარის 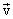. ამიტომ ამ აჩქარებას ხშირად უწოდებენ ცენტრისკენულს. R-ს უწოდებენ სიმრუდის რადიუსს.
სრული აჩქარება განისაზღვრება ტანგენციალური და ნორმალური მდგენელების ვექტორული ჯამით (1.15). რადგან ამ აჩქარებების ვექტორები ურთიერთპერპენდიკულარულია, ამიტომ სრული აჩქარების მოდული იქნება:
 |
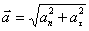(1.18) |
სრული აჩქარების მიმართულება (კუთხე ტრაექტორიის მხებთან) განისაზღვრებ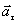ა და 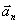ვექტორების სიდიდეების ფარდობით:
