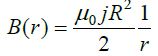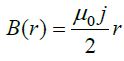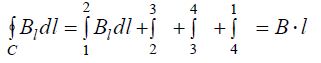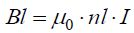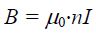როგორც უკვე ავღნიშნეთ ცირკულაციის თეორემის გამოყენება გამართლებულია ბრტყელი ცილინდრული და სფერული სიმეტრიების ამოცანების გადასაჭრელად. ამ შემთხვევებში კონტურის ფორმა (23.1) განტოლებაში შეიძლება დავიყვანოთ ინდუქციის ვექტორის მოდულის კონტურის სიგრძეზე ნამრავლზე. ვნახოთ ეს მაგალითზე.

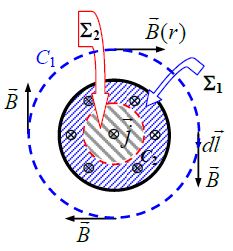
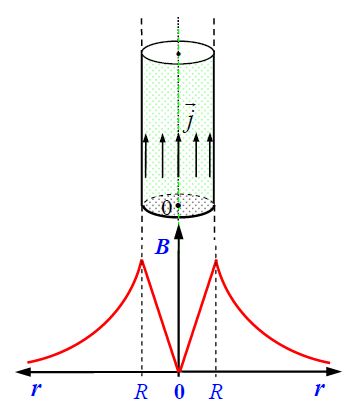
მაგალითი 1. გძელ სწორხაზოვან R რადიუსის მქონე გამტარში გადის დენი. დენის სიმკვრივე თანაბრად არის განაწილებული განიკვეთში და ტოლია j-ს. ვიპოვნოთ მაგნიტური ინდუქციის ვექტორის რადიუსზე დამოკიდებულება გამტარის შიგნით და მის გარეთ.

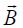
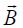
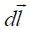
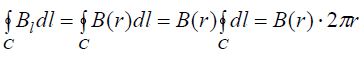
ძალიან გრძელი (მკარცრად რომ ვთქვათ, უსასრულო სიგრძის) გამტარისთვის შეიძლება ამოცანის ცილინდრულ სიმეტრიაზე ვისაუბროთ, ანუ გამტარისადმი პერპენდიკულარულ ნებისმიერ სიბრტყეზე მაგნიტური ველის ძალწირები არის წრეწირები, რომელთა ცენტრები ემთხვევა გამტარს.  ვექტორის მოდული დამოკიდებულია მხოლოდ გამტარიდან  მანძილზე და მოდული მუდმივია ნებისმიერ გამტარზე კონცენტრირებულ წრეწირზე. ავარჩიოთ  კონტური გამტარზე კონცენტრირებული წრის სახით ასე:

ვქტორები  და  ნებისმიერ მის უბანზე თანხვედრილად არიან მიმართულნი, ამიტომ:

 (*)

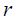
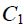
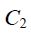
უნდა ვიგულისხმოთ, რომ ინდუქციის -ზე დამოკიდებულების კანონი განსხვავებული უნდა იყოს გამტარის შიგნით და გარეთ. ამიტომ ავარჩიოთ ორი კონტური   და  ასე:

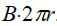
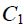
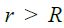
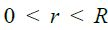
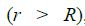
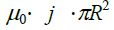
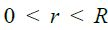
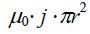
ფორმით მაგნიტური ველის ცირკულაციის გამოსახულება ორივე კონტურისთვის ერთნაირია - . განსხვავება არის მხოლოდ რადიუსის დიაპაზონი (-თვის  , ხოლო -თვის კი ) ხოლო (23.1) განტოლების მარჯვენა ნაწილში -თვის იქნება , ხოლო  ()-თვის კი . 

შედეგად გამტარს გარეთ გვექნება:

ხოლო გამტარს შიგნით კი:

ნახაზზე გამოსახულია ღერძიდან რადიალური მიმართულებით დენიანი გამტარის მაგნიტური ველის ცვლილება. ცხადია ველის მიმართულება ნებისმიერ წერტილში განისაზღვრება მარჯვენა ბურღის წესით.

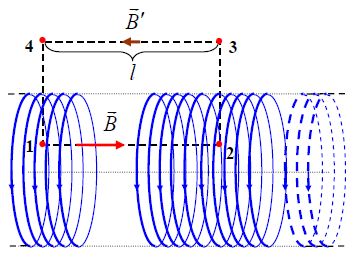
მაგალითი 2. ვიპოვნოთ სოლენოიდის მაგნიტური ინდუქცია

სოლენოიდი წარმოადგენს გრძელ კოჭას რომლის რადიუსი გაცილებით ნაკლებია მის სიგრძეზე. სოლენოიდი შედგება მრავალი ხვიისგა, რომელთაგან თითოეული ქმნის მაგნიტურ ველს და როგორც ჩანს ნახაზიდან სოლენოიდის მაგნიტორი ველი მის შიგნითაც და გარეთაც პარალელურია სოლენოიდის ღერძისადმი. შევარჩიოთ ახლა კონტური 1-2-3-4 ცირკულაციისთვის ისე, რომ მარტივი იყოს ინდუქციის გათვლა. 

ამასტან კონტურის ერთ-ერთი გვერდი 1-2 მოთავსებულია სოლენოიდის შიგნით, ხოლო მეორე 3-4 მის გარეთ. 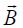  ვექტგორის ცირკულაცია ტგოლია:

ეს ასეა, რადგან მეორე და მეოთხე წევრები ნულებია რადგან მათ ინტეგრალქვეშა ვექტორები ურთიერთპერპენდიკულარულებია და სკალარული ნამრავლები იძლევა ნულს. კონტურის 3-4 მონაკვეთი შეგვიძლოია ავიღოთ სოლენოიდიდან რაგინდ შორს იქ სადაც მაგნიტური ინდუქცია ნულია (ბიო-სავარ-ლაპლასის კანონი) და ამიტომ მეოთხე წევრიც არის ნული. ამიტომ ცირკულაციის გამოსახულება სრულად განისაზღვრება სოლენოიდის შიგნით მაგნიტური ინდუქციით და იგი ტოლი იქნება:

 ან 

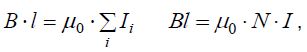
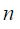
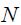
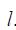
სადაც   არის სოლენოიდის სიგრძის ერთეულზე ხვიების რაოდენობა, ხოლო   არის სოლენოიდის ხვიების სრული რაოდენობა მთელს სიგრძეზე აქედან ვღებულობთ, რომ სოლენოიდის მაგნიტური ინდუქციის მოდული სოლენოიდის შიგნით არის:

3-4 ბნის განლაგებაზე  სოლენოიდის მაგნიტური ინდუქციის დამოუკიდებლობა იმაზე მეტყველებს, რომ სოლენოიდის გარეთ მაგნიტური ველი ძალიან სუსტია, ანუ მთელი მაგნიტური ველი მოქცეულია სოლენოიდის შიგნით. ამ მხრივ სოლენოიდი მაგნიტიზმში თამაშობს ელექტრობაში კონდენსატორის ანალოგიურ როლს.