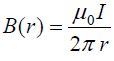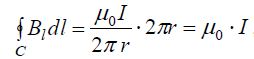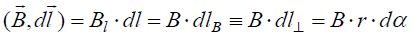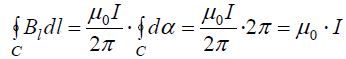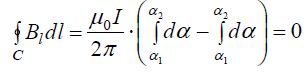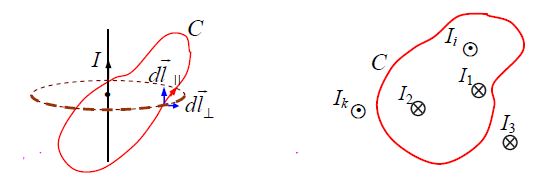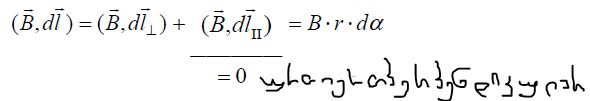გაუსის თეორემის დამტკიცების მსგავსად ნაბიჯ-ნაბიჯ ვაწარმოოთ თეორემის მტკიცება უმარტივესიდან რთულისკენ. 

ა) განვიხილოთ ჯერ უმარტივესი შემთხვევა – მუდმივი დენი უსასრულოდ გრძელ წვრილ სწორხაზოვან სადენში.

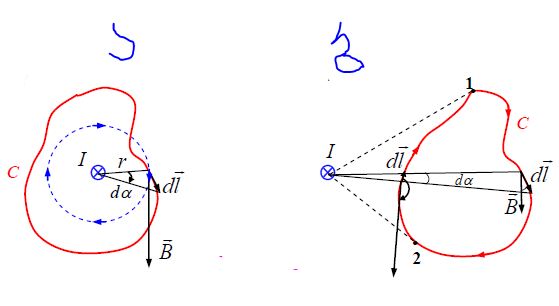
კონტური  არის წრე, რომელიც პერპენდიკულარულია მის ცენტრში გამავალი სადენისადმი. 

 

ცხადია,  კონტური ემთხვევა დენიანი სადენის მაგნიტური ინდუქციის ერთ-ერთ წირს. აქედან ნათელია, რომ ინტეგრების ქვეში პირდაპირ გვექნება წევრი  (კონტურის ნებისმიერ მცირე უბანზე ვექტორების  და  მიმართულებები ერთმანეთს ემთხვევა). ღერძული სიმეტრიის გამო  ინდუქციის ვექტორი დამოკიდებულია მხოლოდ სადენიდან მანძილზე და ამდენად მუდმივია  რადიუსის მზონე წრეწირზე. ამიტომ მისი გამოტანა შეიძლება ინტეგრების ნიშნიდან:

                  (*)

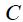
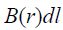
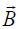
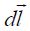
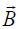
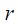
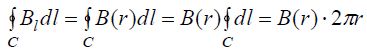
ბიო-სავარ-ლაპლასის კანონისა და სუპერპოზიციის პრინციპის გამოყენების შედეგად უკვე ვიცით, რომ უსასრულოდ გრძელი სწორგაზოვანი დენიანი სადენისთვის 

ამის ჩასმით (*) გამოსახულებაში მივიღებთ:

რაც სწორედ ემთხვევა ჩვენი თეორემის მტკიცებულებას.

ბ) ოდნავ გავართულოთ მდგომარეობა - ვთქვგათ 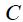 კონტური კვლავ პერპენდიკულარულია უსასრულოდ გრძელი სწორხაზოვანი სადენისა, რომელიც მოთავსებულია კონტურის ფარგლებში, მაგრამ კონტური ამჯერად არის ნებისმიერი ფორმის (ნახ ა)

ჩავწეროთ გეომეტრიული მოსაზრებებიდან გამომდინარე ცხადი გამოსახულებები:

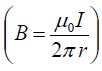
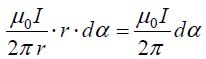
ჩავსვათ მასში მაგნიტური ინდუქციის გამოსახულება უსასრულოდ გრძელი სწორხაზოვანი დენიანი გამტარისთვის. შედეგად მივიღებთ ციურკულაციის გამოსათვლელ ინტეგრალქვეშა გამოსახულებას:

.

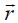
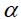
ახლა ამოცანა გამარტივდა, რადგან ერთადერთი ცვლადი დარჩა  რადიუსვექცორის მიერ  კონტურის შემოვლის  კუთხე. მივიღებთ:

რაც ისევ ემთხვევა თეორემის მტკიცებულებას.

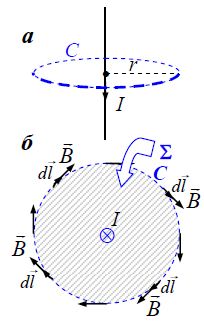
გ) ვთქვათ ახლა გამტარი გადის კონტურს გარეთ (ნახ. ბ).

 კონტური გავყოთ ორ უბნად. ინტეგრალიც გაიყოფა ორ ინტეგრალად და 1 წერტილიდან 2 წერტილში ინტეგრებისას კუთხე   და  ვექტორებს შორის იქნება მახვილი და შესაბამისად მათი სკალარული ნამრავლის ნიშანი იქნება დადებითი, ხოლო წერტილი 2-დან წერტილ 1-ში ინტეგრებისას ლუთხე   და  ვექტორებს შორის იქნება ბლაგვი და მათი სკალარული ნამრავლის ნიშანი იქნება უარყოფითი. საბოლოოდ

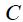
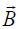
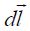
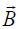
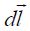
ეს ნიშნავს, რომ კონტურს გარეთ მოქცეულ დენებს ცირკულაციაში წვლილ არ შეაქვთ.

დ) დაგვრჩა განვაზოგადოდ შედეგები, როცა კონტური არ არის ბრტყელი (ადვილი მისახვედრია, რომ შდეგი ამავდროულად ზოგადი იქნება, როცა გამტარი არ არის სწორხაზოვანი) და თვით გამტარები რამდენიმეა (ბევრია).

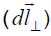
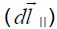
არაბრტყელი კონტურის ნებისმიერი მცირე უბანი შეგვიძლია წარმოვადგინოთ გამტარის პერპენდიკულარული  და პარალელური მდგენელების ჯამით და ამიტომ

შემდგომ კი ბ) და გ) პუნქტების გამოყენება მიგვიყვანს უკვე ცნობილ შედეგებამდე 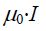კონტურით შემოფარგლული და 0 შემოუფარგლავი დენებისთვის.

ე) დაგვრჩა განვაზოგაგოთ შედეგები ნებისმიერი რაოდენობის დენისთვის.

ამ ნაწილის სამართლიანობა პირდაპირ ჩანს ნახაზიდან და მაგნიტური ინდუქციის ვექტორის სუპერპოზიციის პრინციპიდან. იგივე ითქმის კონტურში დენის ნებისმიერი განაწილებისთვის. ამ შემთხვევაში დენების დისკრეტული მნიშვნელობების ჯამი იცვლება უწყვეტი ინტეგრებით  .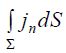

თეორემა დამტკიცებულია!