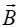ფრანგებმა ბიომ და სავარმა 1820 წელს სხვადასხვა ფორმისა და კონფიგურაციის დენიანი გამტარების მიერ შექმნილი მაგნიტური ველების ინდუქციების განსასაზღვრად ჩაატარეს ცდების სერია. მათ მიღებული ემპირიული იმფორმაციის მდიდარი მასივი გაანალიზა და კანონზომიერები ჩამოაყალიბა ლაპლასმა.
ის მივიდა დასკვნამდე, რომ ნებისმიერი ფორმის დენიანი გამტარის მიერ შექმნილი მაგნიტური ველი შეიძლება განისაზღვროს 
"დენის ელემენტების" მიერ 
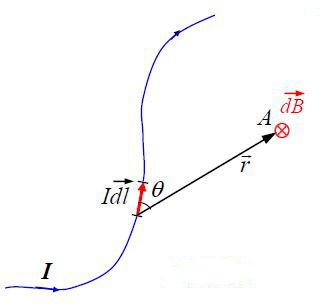
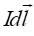
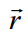რადიუსვექტორით განსაზღვრული სივრცის ნებისმიერ А წერტილში შექმნილი მაგნიტური ველის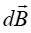 
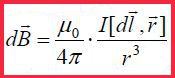
ინდუქციების აჯამვით:
(22.4)
ამ მტკიცებულებამ მიიღო ბიო-სავარ-ლაპლასის კანონის სახელწოდება. პროპორციულობის კოეფიციენტში აქ შედის მუდმივა μ0, რომელიც ტოლია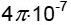 
ვოლტი·სმ/(ამპერი·მეტრი).
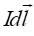
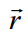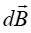
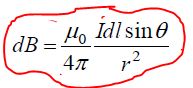
ვექტორის მიმართულება მართობულია როგორც დენის ელემენტისადმი (ვექტორი), ასევე რადიუს-ვექტორისადმი. თუ ჩავთვლით, რომ ნახაზზე წერტილი А დენის ელემენტი ძევს ერთ სიბრტყეზე, მაშინ ვექტორი მიმართულია ჩვენგან ნახაზის სიღრმეში. სასარგებლოა ასევე დავწეროთ რას უდრის დენის ელემენტის მაგნიტური ინდუქციის მოდული:
(22.5)
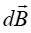
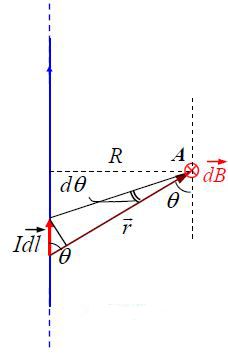
როგორც უკვე ავღნიშნეთ, მთელი დენიანი გამტარის მიერ შექმნილი შედეგობრივი მაგნიტური ველის მოსაძებნად უნდა გამოვიყენოტ სუპერპოზიციის პრინციპი, უნდა მოვძებნოთ ყველა ელემენტის ვექტორების ჯამი. ასეთნაირად პრინციპში შეიძლება გადაწყდეს ნებისმიერი ფორმის დენიანი გამტარის საკითხი. ვაჩვენოთ, როგორ რეალიზდება ეს მიდგომა პრაქტიკულად არართული ფორმის გამტარებისთვის.
მაგალითი 1. ვიპოვნოთ გრძელი სწორხაზოვანი დენიანი გამტარის მაგნიტური ველის ინდუქცია.
"დავყოთ" გამტარი მცირე ელემენტებად და ბიო-სავარ-ლაპლასის კანონის შესაბამისად ვიპოვნოთ თითოეული ელემენტისთვის А წერტილში ვიპოვნოთ მაგნიტური ველის ინდუქცია. ვექტორების მიმართულებებს განვსაზღვრავთ ბურღის წესით (მარჯვენა ხრახნი).
სანამ ვექტორების აჯამვის პროცესზე გადავალთ ავღნიშნოთ, რომ ყველა ისინი მიმართულია ერთნაირად – იმ სიბრტყის მართობულად, რომელზეც მოთავსებულია А წერტილი (ნახაზზე მითითებულია 
სიმბოლოთი და ნიშნავს რომ ვექტორი მიმართულია ჩვენგან ნახაზის სიბრტყის სიღრმეში) და დენიანი გამტარი. ამიტომ შედეგობრივი ვექტორი 
მიმართულია ასევე და შეიძლება ავჯამოთ სკალარული სიდიდეები – 
მოდულები. ამ აჯამვის (ინტეგრირების) შესასრულებლად, გამოვსახოთ (22.5) გამოსახულებაში შემავალი სიდიდეები 
და 
მხოლოდ ერთადერთი ცვლადით – 
და მისი დიფერენციალით dθ :
.
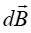
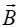
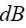
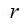
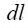
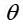
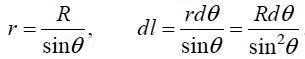
ჩავსვათ ყოველივე ეს (22.5)-ში, შევასრულოთ ცხადი შეკვეცები და მივიღებთ:
.
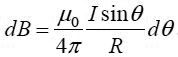
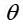
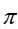
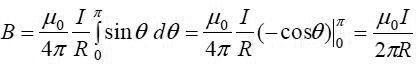
დარჩა მხოლოდ შევასრულოთ კუთხის ცვლილების საზღვრებში ინტეგრირება. ძალიან გრძელი დენიანი გამტარის შემთხვევაში ანუ როცა იცვლება 0-დან 
-მდე:
.
როგორც ვხედავთ, ძალიან გრძელი დენიანი გამტარის ინდუქცია იცვლება მისგან დაშორების უკუპროპორციულად, ვექტორების მიმართულებაზე უკვე ვისაუბრეთ, მაგრამ შემდეგში სურველია უფრო თვალსაჩინოდ წარმოვიდგინოთ მაგნიტური ველის სტრუქტურა.