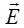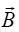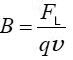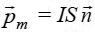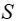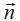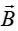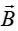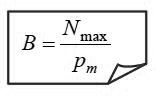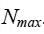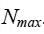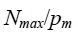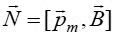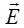ელექტრული ველის დაძაბულობის ანალოგიით შემოვიტანოთ მაგნიტური ველის ძალური მახასიათებელი – 
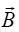მაგნიტური ინდუქციის ვექტორი . ანუ, საფუძვლად ვიღებთ ძალას, რომელიც მოქმედებს "საცდელ მუხტზე", მხოლოდ ამჯერად მოძრავზე! სკოლის კურსიდანაც გვახსოვს, რომ ამ ძალის მაგნიტურ მდგენელს უწოდებენ ლორენცის ძალას, ის პროპორციულია ნაწილაკის სიჩქარისა და მუხტის სიდიდის. ელექტრული ველის დაძაბულობის განსაზღვრების ანალოგიით თანმიმდევრული იქნებოდა მაგნიტური ველის განსაზღვრა ასე: 
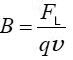და, მიმართულების დადგენა კი ლორენცის ძალისა და ნაწილაკის სიჩქარის მეშვეობით შეთანხმებით. მაგრამ პრაქტიკულად ეს მოუხერხებელია, რადგან ლორენცის ძალა მცირეა და შესამჩნევი ხდება მხოლოდ დამუხტული ნაწილაკების ძალიან დიდი სიჩქარეებისთვის.
ამიტომ მაგნიტური ინდუქციის განსამარტად სხვა საშუალებას მივმართავთ. უკვე ვიცით, რომ მაგნიტური ველი მაორიენტებელ გავლენას ახდენს კომპასის ისარზე. პრაქტიკაში უფრო მოსახერხებელია ისრის ნაცვლად მცირე დენიანი ჩარჩოს გამოყენება (ის არსობრივად იგივეა რაც კომპასის ისარი) - როგორც "საცდელი ხვია".
(განსაზღვრება) საცდელი ხვია ეწოდება მცირე ზომის დენიან ჩარჩოს. საცდელი ხვიის მაგნიტურ მომენტს უწოდებენ ვექტორს, რომელიც ტოლია
,
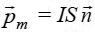სადაც I არის ხვიაში გამავალი დენის ძალა,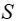 
– ჩარჩოს ფართობი, ხოლო 
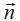– ჩარჩოსადმი "ერთეულოვანი დადებითი ნორმალი". დადებითი ნორმალი მიმართულია მარჯვენა ბურღის გადაადგილების მიმართულებით, როცა მის სახელურს ვაბრუნებთ ჩარჩოში დენის მიმართულებით. როგორც კომპასის ისარი, საცდელი ხვიაც შემობრუნდება მაგნიტურ ველში მაბრუნებელი ძალების მოქმედების შედეგად. მაგნიტური ველის ძალური მოქმედება დენიან გამტარებზე და მოძრავ მუხტებზე განსაზღვრავს სწორედ მაგნიტური ველის ინდუქციის ვექტორს.
(განსაზღვრება) მაგნიტური ველის ინდუქციის ვექტორი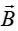 
:
1. 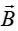ვექტორის მიმართულებად მიჩნეულია საცდელი ხვიის 
მაგნიტური მომენტის მიმართულება.
2. მაგნიტური ინდუქციის ვექტორის მოდული საცდელ ხვიაზე მაგნიტური ველისგან მოქმედი ძალების მაქსიმალური მომენტის საცდელის ხვიის მაგნიტურ მომენტთან ფარდობის ტოლია:
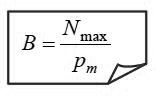(22.1)
♦ შენიშვნები
1. ცდა აჩვენებს, რომ ძალების ეს მომენტი დამოკიდებულია საცდელი ხვიის საწყის ორიენტაციაზე. ის მაქსიმალურია, როცა 
. (14.1) თანაფარდობის მრიცხველში სწორედ ძალის მომენტის მაქსიმალური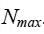 
მნიშვნელობა ზის.
2. ცდიდან ასევე ცნობილია, რომ სიდიდე 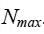, თავის მხრივ, დენიანი ჩარჩოში გამავალი დენის ძალისა და ჩარჩოს ფართობის ნამრავლის პროპორციულია. ხვიის ფორმაზე ის დამოკიდებული არ არის! ფარდობა 
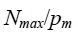– მაგნიტური ინდუქციის მოდული – არ არის საცდელი ხვიის თვისებებზე დამოკიდებული, არამედ დამოკიდებულია მხოლოდ თვით მაგნიტურ ველზე.
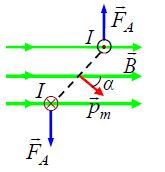
3. \(\alpha\) კუთხის ნებისმიერი მნიშვნელობის დროს ძალების მომენტის მოდული ტოლია 
, ხოლო თვით ვექტორი
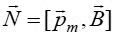. (22.2)
უკანასკნელი ტოლობა იძლევა დენიან ჩარჩოზე მოქმედი ძალების მომენტის გამოთვლის საშუალებას – "მაგნიტური დიპოლი" გარე მაგნიტურ ველში.