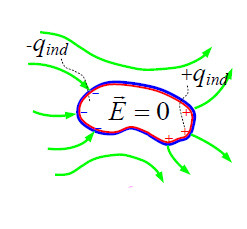
ნახაზი თვალნათლივ გვიხსნის ამ მოვლენის არსს. გამტარის იმ ნაწილის ზედაპირზე, რომელიც ახლოს იმყოფება დადებით დამუხტულ გარეშე სხეულთან გროვდება თავისუფალი ელექტრონები, ხოლო მის საპირისპირო მხარეს წარმოიქმნება ელექტრონების დეფიციტი ანუ ის ზედაპირი ხდება დადებითად დამუხტული. წინა თავის 1 – 5 დებულებები ამ შემთხვევაშიც ძალაშია იმ განსხვავებით, რომ ამჟამად სხეულს არ აქვს ჭარბი მუხტი.

დებულება 3-ის თანახმად ჭარბი მუხტი ლოკალიზებულია თხელ ზედაპირულ ფენაში. იგივე შეიძლება ითქვას ინდუცირებულ მუხტზე. აქედან გამომდინარეობს კიდევ ერთი გარემოება: თუ გამტარს ნებისმიერ შიდა ნაწილს ამოვაცლით, ეს არანაირად არ აისახება მუხტების წონასწორობაზე გამტარში და ელექტრულ ველზე გამტარში და მის გარეთ. ამ შემთხვევაში ადგილი აქვს ე.წ. „გამტარი გარსის“ არსებობას. მოვიტანოთ რამდენიმე დებულება გამტარ გარსებზე, რომელთაც ხანდახან თეორემებს უწოდებენ ან ერთობლივად უწოდებენ ფარადეის თეორემას.

· ა) თუ გამტარი გარსის შიგნით არ არის დამუხტული სხეულები, მაშინ სივრცის ეს ნაწილი თავისუფალია ელექტრული ველისგან

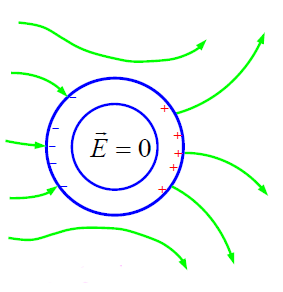
ანუ, ველი, რომელიც შექმნილია გამტარის გარეთ მყოფი დამუხტული სხეულებით, არ აღწევს გამტარით შემოფარგლულ სივრცეში. ეს საფუძვლად უდევს ე.წ. „ელექტროსტატიკურ დაცვას“. გამტარით შემოფარგლულ სივრცეში შეიძლება მოთავსდეს ელექტრული სქემები, მოწყობილობები და გამზომი ხელსაწყოები ან თვით ექსპერიმენტატორიც. ამ შემთხვევაში გარსის შიგნით მოთავსებული ექსპერიმენტი დაცული იქნება გარე ელექტრული ველის ზემოქმედებისგან. რა მოხდება თუკი გარსის შიგნით ღრუში მოვათავსებთ დამუხტულ სხეულებს. ამ შემთხვევაში ღრუში ველი რა თქმა უნდა გაჩნდება.

·ბ) ჯამური მუხტი, რომელიც ინდუცირდება ღრუს შიდა ზედაპირზე, ტოლია ღრუს შიგნით არსებული მუხტების ალგებრული ჯამისა შებრუნებული ნიშნით. 

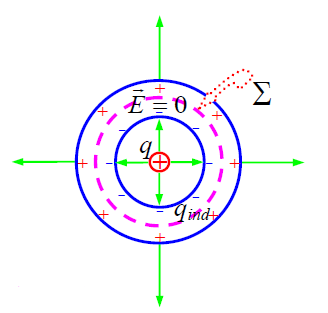
ამ დებულების დასასაბუთებლად საკმარისია გამტარი გარსის შიდა და გარე ზედაპირებს შორის შერჩეული ნებისმიერი ჩაკეტილი S ზედაპირისთვის გამოვიყენოთ გაუსის თეორემა. რადგან გამტარის შიგნით ნებისმიერ წერტილში დაძაბულობა არის ნულის ტოლი ამიტომ ნულია ინტეგრალიც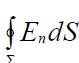  

, ანუ დაძაბულობის ვექტორის ნაკადი. შესაბამისად ნულია ამ ზედაპირის შიგნით ჯამური მუხტი:

ღრუს შიგნით ჯამური მუხტი +

გარსის შიდა ზედაპირზე ინდუცირებული მუხტი  = 0.

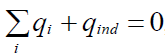
სწორედ აქედან გამომდინარეობს თეორემის მტკიცებულებაც, ანუ:

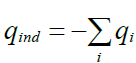    (18.4)

გამტარის სრული მუხტის შენახვიდან (გარსი დამუხტული არ არის!) გამომდინარეობს კიდევ ერთი დებულება.

· გ) ინდუცირებული მუხტი, რომელიც გარსის გარე ზედაპირზე წარმოიქმნება, მოდულით ტოლია და ნიშნით საწინააღმდეგო იმ მუხტისა, რომელიც ინდუცირდება გარსის შიდა ზედაპირზე

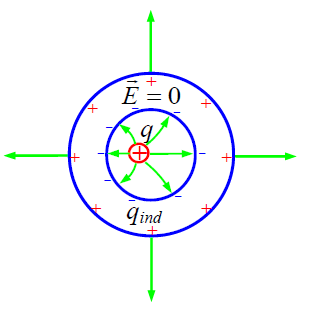
სხვაგვარად რომ ვთქვათ, ის ზუსტად უდრის იმ მუხტს, რომელიც მოთავსებული გარის შიგნით ღრუ სივრცეში. გარსის შიგა ზედაპირზე ინდუცირებული მუხტის განაწილება დამოკიდებულია ღრუში არსებული მუხტების განაწილებაზე და გარსის ფორმაზე. ხოლო გარე გარსზე მუხტების განაწილება გამომდინარეობს მხოლოდ მისი ფორმიდან და არანაირად არ არის ღრუში მუხტების განაწილებაზე დამოკიდებული. გარე ზედაპირზე მუხტები განცალკევებულია ყველა მუხტისგან შიგნით სადაც ელექტრული ველი არ არის!