მუშაობა თერმოდინამიკაში

თერმოდინამიკაში სხეულის როგორც მთლიანის მოძრაობა არ განიხილება და საუბარი არის მაკროსკოპული სხეულის ნაწილების ერთმანეთის მიმართ გადაადგილებაზე.   მუშაობის შესრულებისას იცვლება სხეული მოცულობა, ხოლო მისი სიჩქარე რჩება ნულის ტოლი. სხეულის მოლეკულების სიჩქარე კი იზრდება! ამიტომ იცვლება სხეულის ტემპერატურა. მიზეზი ის არის, რომ მოძრავ დგუშთან შეჯახებისას (აირის შეკუმშვა) მოლეკულების კინეტიკური ენერგია იცვლება - დგუში გადასცემს თავისი მექანიკური ენერგიის ნაწილს. დაშორებად დგუშთან შეჯახებისას (გაფართოება) მოლეკულების სიჩქარე მცირდება, აირი ცივდება. მუშაობის შესრულებისას თერმოდინამიკაში იცვლება მაკროსკოპული სხეულების მდგომარეობა: მათი მოცულობა და ტემპერატურა.

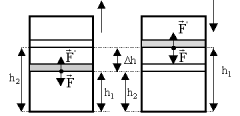
\(\dpi{120} \vec{F}\) - დგუშით აირზე მომქმედი ძალა.

А - გარეშე ძალებით აირის შეკუმშვაზე გაწეული მუშაობა.

\(\dpi{120} \vec{F}{}'\)- დგუშზე აირით მოქმედი ძალა.

А' - აირის გაფარტოებაზე გაწეული მუშაობა.

\(\dpi{120} \vec{F}\)= -\(\dpi{120} \vec{F}{}'\)  - ნიუტონის მესამე კანონის მიხედვით.

შესაბამისად: А= - А'

\(\dpi{120} \vec{F}{}'\)= pS, სადაც p- წნევაა, S - დგუშის ფართობია.

თუ გაზი ფართოვდება:

Δh=h₂ - h₁  - დგუშის გადაადგილებაა. V₁=Sh₁; V₂=Sh₂.

მაშინ: A'=F'Δh=pS(h₂ - h₁)=p(Sh₂ - Sh₁)=p(V₂-V₁)=pΔV

გაფართოებისას გაზის მუსაობა დადებითია. შეკუმშვისას  - უარყოფითი. ასე რომ: A' = pΔV     - გაზის მუშაობაა

A= - pΔV  - გარეშე ძალების მუსაობაა.

კლაპეირონის განტოლების გამოყენებით, მივიღებთ: 

\(\dpi{120} A=p\Delta V=p\frac{\nu R\Delta T}{p}=\nu R\Delta T\)

ეს გამოსახულებები სამართლიანია მოცულობის ძალიან მცირე (!) ცვლილებებისას ან მუდმივი წნევისას (ანუ იზობარულ პროცესში)

უნივერსალური გაზური მუდმივას ფიზიკური არსი.

\(\dpi{120} R=\frac{A}{\nu \Delta T}\) - უნივერსალური გაზური მუდმივა რიცხობრივად 1 მოლი იდეალური გაზის მიერ მისი 1 კ-ით იზობარული გათბობის დროს შესრულებული მუშაობის ტოლია.

მუშაობის გეომეტრიული ინტერპრეტაცია

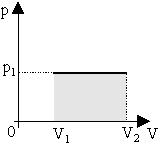
იზობარულ პროცესში p,V გრაფიკის ქვეშა ფართობი რიცხობრივად მუშაობის ტოლია (სიჩქარის გრაფიკზე გადაადგილების ანალოგიურად).

ზოგადად პროცესი უნდა დავყოთ მცირე ნაწილებად და გამოვთვალოთ ელემენტალური მუშაობები, ხოლო შემდეგ ისინი სევკრიბოთ (ინტეგრირების პროცესი):

მაგალითად, იზოთერმულ პროცესში .

იზოქორულ პროცესში მოცულობა არ იცვლება, შესაბამისად, იზოქორულ პროცესში მუშაობა არ სრულდება!

 ადიაბატურ პროცესში .
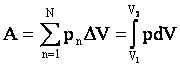
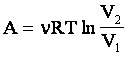
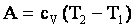