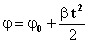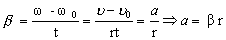| ცენტრისკენული აჩქარება | ||
|
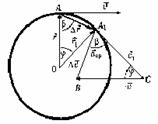
გამოვთვალოთ აჩქარების სიდიდე წრეწირზე წერტილის თანაბარი მოძრაობის დროს და ვიპოვნოთ მისი მიმართულება. ვთქვათ დროის რაღაც t შუალედში სხეული გადაადგილდა А წერტილიდან А1 წერტილში მოდულით მუდმივი სიჩქარით. გამოვსახოთ ამ წერტილებში სიჩქარის ვექტორები და ვიპოვნოთ სიჩქარის ცვლილების ვექტორი განვიხილოთ АА1О და А1СВ სამკუთხედები. ეს სამკუთხედები ტოლფერდებია და წვეროს კუთხეები ურთიერთტოლია რადგან АО┴СВ და А1О┴А1С (კუთხეები ურთიერთპერპენდიკულარული გვერდებით). შესაბამისად, ეს კუთხეები არიან მსგავსნი. სამკუთხედების მსგავსებიდან გამომდინარეობს შემდეგი პროპორცია: ტოლობის მარჯვენა და მარცხენა მხარეები გავყოთ იმდ დროის შუალედზე, რომელშიც მოხდა გადაადგილება და გავითვალისწინოთ, რომ |
მაგალითები: - დედამიწა საკუთარი ბრუნვის ღერძის ირგვლივ ბრუნვის დროს аცკ=0,03 მ/წმ2, - დედამიწა მზის ირგვლივ ბრუნვის დროს аცკ=0,006 მ/წმ2, - მზის სისტემა გალაქტიკის ცენტრის ირგვლივ ბრუნვის დროს аცკ=3.10-10 მ/წმ2.
|
|
|
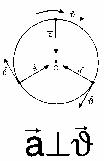
ახლა განვსაზღვროთ აჩქარების მიმართულება. რადგან აჩაქრების განსაზღვრისთვის უნდა ავიღოთ ზღვარი, როცა Δt→0, ამიტომ ნახატიდან ჩანს, კუთხე φ წავა შემცირებისკენ (→0), ხოლო b→900. ეს ნიშნავს, რომ А1В წრფე (ვექტორი შესაბამისად, წრეწირზე თანაბარი მოძრაობისას აჩქარების ვექტორი მიმართული წრეწირის ცენტრისკენ (ბრუნვის ცენტრისკენ). ამიტომ აჩქარებას ეწოდება ცენტრისკენული აჩქარება. |
 |
|
|
ცენტრისკენული აჩქარება ცვლის სიჩქარის მხოლოდ მიმართულებას და არა სიდიდეს. ცენტრისკენული აჩქარების ვექტორი სიჩქარის ვექტორის პერპენდიკულარულია. კუთხური და წირით სიჩქარეებს შორის კავშირის გამოყენებით მივიღებთ: |
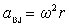 |
|
|
თანაბრადცვლადი მოძრაობა წრეწირზე ამ მოძრაობისთვის ყველა განტოლება მიიღება წრფივი თანაბრადცვლადი მოძრაობის ანალოგიით. |
||
|
წრფივი თანაბრადცვლადი მოძრაობა.
|
წრეწირზე თანაბრადცლადი მოძრაობა.
|
|

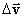 .
. 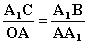 ანუ, გადავალთ რა ფიზიკურ აღნიშვნებზე, მივიღებთ
ანუ, გადავალთ რა ფიზიკურ აღნიშვნებზე, მივიღებთ 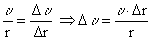 .
.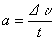 და
და 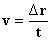 . მაშინ:
. მაშინ: 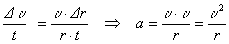 .
.
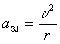
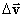
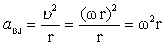 .
.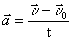
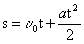
 - კუთხური აჩქარება (რად/წმ2)
- კუთხური აჩქარება (რად/წმ2)