| შეკითხვა: | უმასო ღეროზე დამაგრებულ სხეულს თანაბრად აბრუნებენ წერეწირზე ვერტიკალურ სიბრტყეში. როცა სხეული A წერტილშია( ზედა მდგომარეობა), ღერო შეკუმშულია. ღეროს დრეკადობის ძალა ამ წერტილის გავლისას 3-ჯერ განსხვავდება დრეკადობის ძალისგან ქვედა B წერტილის გავლის მომენტში. გამოთვალეთ ამ სხეულის აჩქარება C წერტილის გავლისას. (C წერტილი მდებარეობს A წერტილიდან 60 გრადუსის დაშორებით.) ამ წერტილში საით არის მიმართული აჩქარება? თუ ამბობენ თანაბრად მოძრაობსო ცენტრისკენ უნდა იყვეს მაგრამ ძალების ტოლქმედი საითაა? და საერთოდ, რა განსხვავებაა ღეროსა და თოკს შორის? |
|---|---|
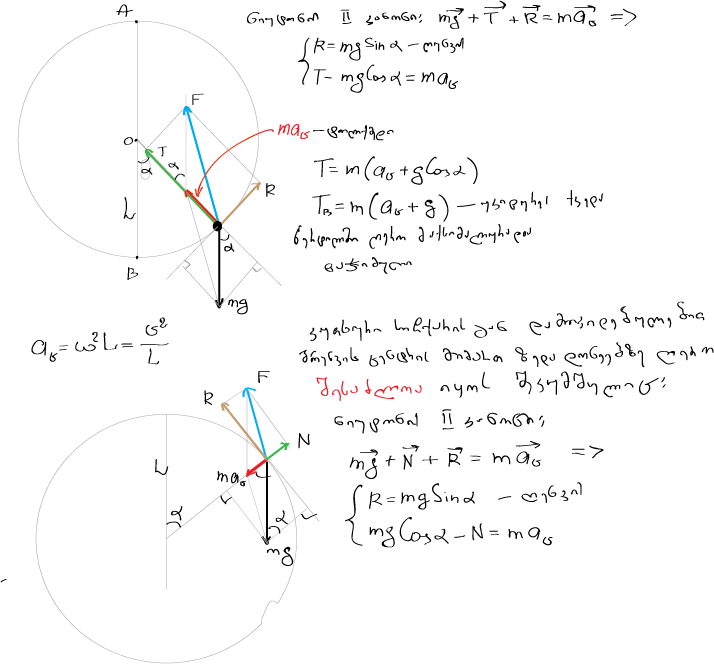
| პასუხი: | მიუხედავად იმისა რომ ჩემს იუმორს ხანდახან მწყრალად აღიქვამ, მაინც ვიტყვი, რომ თვალების ''გამისაჩიჩქნ" კითხვებს სვამ... ანუ საინტერესოს... მაგრამ ამ კითხვების ''დასაამებელი'' პასუხებიც არსებობს. და საერთოდ, რა განსხვავებაა ღეროსა და თოკს შორის? .... თოკში(ძაფში) შესაძლებელია მხოლოდ გაჭიმულობის დრეკადობის აღძვრა, ღეროში კი როგორც გაჭიმულობის ასევე კუმშვის და კიდევ ღუნვა - გრეხის დრეკადობის აღძვრაც... დასტური ამ განსახვავებისა არის ერთი ასეთი ტრივიალური ამოცანა(რომელიც შენთვის ცნობილი იქნება): რა მინიმალური ჰორიზონტალური სიჩქარე უნდა მივანიჭოთ L სიგრძის ძაფზე(ღეროზე) დაკიდებულ სხეულს, რათა მან შეძლოს ბრუნვა ვერტიკალურ სიბრტყეში? ა) ძაფზე დაკიდებულ სხეულს უნდა მივანიჭოთ vmin = \(\sqrt{5gL}\) სიჩქარე... ძაფი ყველა წერტილში უნდა დაჭიმული იყოს და უკიდურეს ზედა წერტილში( სადაც დაჭიმულობა განულდება) მას ექნება სიჩქარე -- \(\sqrt{gL}\)... ეს მოძრაობა აჩქარებულია ორივე ფაქტორის გამო: იცვლება როგორც სიჩქარის მიმართულება ასევე სიჩქარის მოდულიც და შესაბამისად გვაქვს აჩქარების როგორც ცენტრისკენული ასევე მხებითი მდგენელები... და ეს გამოწვეულია სიმძიმის და ძაფის დაჭიმულობის ძალების მოქმედებით. ბ) ღეროზე დაკიდებულ სხეულს კი საკმარისია მივანიჭოთ vmin = \(\sqrt{4gL}\) სიჩქარე და ეს საკმარისობა ზუსტად იმითაა გამოწვეული, რომ უკვე საქმე გვაქვს ღეროსთან. ამ დროს უკვე საკმარისია სხეულმა ''რის ვაივაგლახით'' მაგრამ როგორმე მიაღწიოს უკიდურეს ზედა წერტილს სადაც სიჩქარე განულდება და ეს მოხდება მხოლოდ იმის ხარჯზე, რომ უკიდურესი ზედა წერტილიდან ქვევით L/3 დონეზე ღეროს დაჭიმულობა იცვლება კუმშვით--- ქვედა 5L/3 უბანზე ღერო დაჭიმულია ხოლო ზედა L/3 უბანზე კი შეკუმშული. ძაფის შემთხვევაში კი ამ დროს სხეული ''მოწყდებოდა'' წრეწირს - პარაბოლით ქვემოდან ჩაუვლიდა წრეწირის უკიდურეს ზედა წერტილს.... დანარჩენი ყველაფერი კი ძაფის შემთხვევის ანალოგიურია: მოძრაობა აჩქარებულია ორივე ფაქტორის გამო: იცვლება როგორც სიჩქარის მიმართულება ასევე სიჩქარის მოდულიც და შესაბამისად გვაქვს აჩქარების როგორც ცენტრისკენული ასევე მხებითი მდგენელები . საქმე უკვე სხვაგვარადაა ღეროზე დამაგრებული სხეულის თანაბარი ბრუნვისას ვერტიკალურ სიბრტყეში(მაგ საათის ისარი)... სცენაზე შემოდის ღეროს ღუნვის დრეკადობა... (აპლოდისმენტები...) ამ წერტილში საით არის მიმართული აჩქარება? თუ ამბობენ თანაბრად მოძრაობსო ცენტრისკენ უნდა იყვეს .... აბა მუჭო?!!! და არა მარტო ამ წერტილში, არამედ იმ წერტილშიც და... იმის ამის აქეთურა თუ იქეთურა -ზედოურა თუ ქვედოურა წერტილებშიც... წრეწირის ნებისმიერ წერტილში გვექნება მხოლოდ ცენტრისკენული აჩქარება(მხებითი-ტანგენციალური კი არა) მაგრამ ძალების ტოლქმედი საითაა?..... ვფიქრობ ჩვენთვის პატივცემულ ნიუტონს მუხლები არ აუკანკალდება და .... ცენტრისკენ! ისღა დაგვრჩენია ავაგოთ ისეთი ნახაზი რომელზეც სხეულზე მოქმედი mg სიმძიმის ძალის და ღეროს მხრიდან მოქმედი F ძალის ტოლქმედი მიმართული იქნება წრეწირის ცენტრისკენ და შემდეგ ინტერესის გამო ეს F ძალა დავშალოთ ღეროს გასწვრივი T დაჭიმულობის(ან ზედა უბანში შესაძლო N კუმშვის) და ღეროს მართობული R ღუნვის დრეკადობის ძალების მდგენელებად.
T = 3N....... T - mg = maც ....... mg - N = maც....------>>>> aც = g/2 ---------- ყველა წერტილში ერთნაირია --------------------------------- ოლეგი გაბრიაძე |