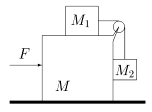
სურათზე გამოსახულ სისტემაში

ხახუნი არსად არ არის. რა მუდმივი, ჰორიზონტალური ძალა უნდა მოვდოთ  მასის სხეულს, იმისთვის რომ  მასის სხეულის მიმართ  და  მასის სხეულები უძრავი იყოს? რა აჩქარებით დაიწყებს ამ შემთხვევაში მთელი სისტემა მოძრაობას? თოკი უჭიმვადია და არ აქვს მასა, მასა არ აქვს ჭოჭონაქსაც და ხახუნის ძალა ჭოჭონაქსა და თოკს შორის 0-ის ტოლია.

რადგან \(M_{2}\) მასის სხეული \(M\) მასის სხეულის მიმართ არც ქვევით უნდა ჩამოვიდეს და არც ზევით ავიდეს, ამიტომ \(M_{2}g=T\), სადაც \(T\) ვერტიკალური თოკის დაჭიმულობის მოდულია. რადგან ამოცანის პირობის დანახმად თოკი უჭიმვადი და უმასოა, ჭოჭონაქს მასა არ აქვს და არც ხახუნი, ამიტომ თოკის დაჭიმულობის მოდული მთელ მის სიგრძეზე ერთნაირია. მაშინ \(M_{1}\) მასის სხეული იმოძრავებს ჰორიზონტალური აჩქარებით \(M_{1}a=T=M_{2}g\Rightarrow a=\frac{M_{2}g}{M_{1}}\). \(M_{1}\) და \(M_{2}\) მასის სხეულები \(M\) მასის სხეულის მიმართ არ უნდა მოძრაობდნენ, ამიტომ \(F\) ძალის სიდიდე ისეთი უნდა იყოს, რომ ამ სხეულების სისტემას, რომლის მასაც არის \(M_{1}+M_{2}+M\) მიენიჭოს აჩქარება \(a=\frac{F}{M_{1}+M_{2}+M_{3}}=\frac{M_{2}g}{M_{1}}\). მაშინ \(F\) ძალა ტოლი უნდა იყოს \(F=\frac{M_{2}g(M+M_{1}+M_{2})}{M_{1}}\).