ბატონო ოლეგ, თუ არ შეწუხდებით იქნებ შეძლებისდაგვარად ამიხსნათ რაციონალური უტოლობის ამოხსნა ინტერვალთა მეთოდით...კონკრეტულად ინტერვალების ნიშნების დადგენა...წინასწარ დიდი მადლობა   <3

1)   უტოლობა დავიყვანოთ   \(\frac{f(x)}{g(x)}\geqslant (\leqslant )0\)  სახეზე..... მაგ  \(\frac{(x^{4}-10000)(100-20x-3x^{2})}{x^{3}(3x^{2}-16x+20)}\leqslant 0\)

2)  მამრავლი მრავალწევრები   აუცილებლად  დავშალოთ   ფესვის  შემცველი ორწევრების ნამრავლად(თუ ეს ფესვები არსებობენ), ისე რომ  x-ს კოეფიციენტი  იყოს +1....

\(x^{4}-10000=(x^{2}-1)(x^{2}+1)=(x-1)(x+1)(x^{2}+1)\)

\(100-20x-3x^{2}=-3(x+10)(x-\frac{10}{3})\)

\(3x^{2}-16x+20=3(x-2)(x-\frac{10}{3})\)

შესაბამისად  უტოლობა მიიღებს სახეს:      \(\frac{-3(x-10)(x+10)^{2}(x^{2}+100)(x-\frac{10}{3})}{3(x-0)^{3}(x-2)(x-\frac{10}{3})}\leqslant 0\)

4)   უტოლობიდან  გაყოფის გზით ''ამოვყაროთ'' ის მამრავლები, რომლებიც ინარჩუნებენ  მუდმივ ნიშანს...... რადგანაც   ნებისმიერი  x-თვის      - (x² +100) < 0 , ჩვენი უტოლობის ორივე მხარის    - (x² +100) -ზე გაყოფის

შედეგად  უტოლობის ნიშანი შეიცვლება და მივიღებთ                    \(\frac{(x-10)(x+10)^{2}(x-\frac{10}{3})}{(x-0)^{3}(x-2)(x-\frac{10}{3})}\geqslant 0\)     როგორც აღვნიშნე    x -ის კოეფიციენტი    ყველგან არის   +1

5)   დავადგინოთ ფესვთა ლუწ-კენტობის საკითხი:    გვაქვს   5 ფესვი ....

 x=10 ....  იგი კენტი რიგისაა  -  მხოლოდ ერთხელ გვხვდება  უტოლობაში, რაც იმას ნიშნავს, რომ    x-10  ორწევრის მნიშვნელობა     10--ს მარცხნივ უარყოფითია და მარჯვნივ კი  დადებითი

x= -10....  იგი ლუწი რიგისაა - ორჯერ   მეორედება უტოლიბაში - წარმოდგენილია კვადრატში (x + 10)² , რაც იმას ნიშნავს რომ   (x + 10)² -ის მნიშვნელობა      - 10 მარცხნივაც  და მარჯვნივაც  დადებითია

x= 10/3 .... იგიც    ლუწი რიგისაა - ორჯერ   მეორედება უტოლიბაში - მრიცხველშიც არის და მნიშვნელშიც,   რაც  იმას ნიშნავს რომ       10/3 -ის   ორივე მხარეს      ( x-10/3) / (x- 10/3) - ის  მნიშვნელობა   დადებითია (კერძოდ ეს მნიშვნელობაა  1 )

p.s.    აქ შესაძლებელი იყო    მრიცხველისდა მნიშვნელის      ( x-10/3) -ზე  შეკვეცაც  იმის აუცილებელი მითითებით, რომ   x \(\neq\) 10/3   და   თუ საჭირო   გახდებოდა   საბოლოო ამონახსენიდან    ამოგვეგდო   ეს  წერტილი.

x = 0 და   x = 2   ფესვებიც   კენტი რიგისაა.

6)     დავიტანოთ ხუთივე  ფესვი      x -თა ღერძზე    მათი ლუწ-კენტობის მითითებით  და  უკიდურესი მარჯვენა   ფესვის  (+10)  მარჯვნივ და ზემოდან    დავიწყოთ ინტერვალთა მეთოდის  შესაბამისი  წირის  შემოვლება.    ამ წირით მიმდევრობით უნდა გავიაროთ  ყველა ფესვი  მარჯვნიდან მარცხნივ..... 

 ა)  კენტი რიგის ფესვის გავლისას   წირით  გადავკვეთოთ     x ღერძი   და  წირითვე   მივიდეთ  უახლოეს მარცხენა მეზობელ  ფესვთან

ბ)   ლუწი რიგის   ფესვის გავლისაას   წირით  არ გადავკვეთავთ   x ღერძს და  და იგივე მხრიდან(ზემოდან ან ქვემოდან)  მივიდეთ     უახლოეს მარცხენა მეზობელ  ფესვთან..

და ასე შემდეგ    გავიაროთ   უკიდურესი  მარცხენა ფესვიც  და  მის შემდეგ წირი გავაგრძელოთ    მარცხნივ   (შესაბამისად  ზემოთ ან ქვემოთ )

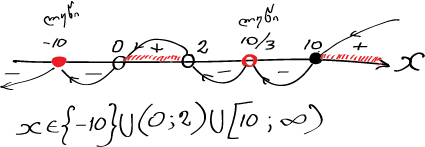
ჩვენს მაგალითში  ფესვები    დალაგებულია    მარჯვნიდან მარცხნივ შემდეგი თანმიმდევრობით        +10(კენტი).....+10/3 (ლუწი) .....+2(კენტი).....0(კენტი).....  - 10(ლუწი) 

(სასურველია    +10 და  -10  წერტილები გაამუქო, რამეთუ ისინი ჩვენს  არამკაცრ  უტოლობაში   ტოლობას შეესაბამებიან- ამონახსნები არიან, ხოლო   დანარჩენები კი  პატარა  რგოლებით აღნიშნო - ამონახსნები  არ არიან)

+10 -ის  მარჯვნივ და ზემოდან  წირით   გადავკვეთავთ    +10 წერტილს და წირით  უკვე   ქვემოდან მივალთ   +10/3 წერტილამდე....  შემდეგ

 წირით არ გადავკვეთავთ ამ წერტილს და ქვემოდანვე  წირით მივალთ  +2 წერტილამდე.... შემდეგ

წირით გადავკვეთავთ   ამ წერტილს და უკვე ზემოდან მივალთ   0 წერტილამდე.... შემდეგ 

წირით გადავკვეთავთ   ამ წერტილს და უკვე ქვემოდან მივალთ    -10 წერტილამდე ... შემდეგ

წირით   არ გადავკვეთავთ ამ წერტილს   და წირს გავაგრძელებთ  ისევ ქვემოთ და მარცხნივ ....

ახლა კი გაჩერდი და კარგად ამოისუნთქე.......ჰუუუ!

შემოვლებული     წირის   x  ღეძის მიმართ       ზედა    უბნის     შესაბამისი   x -ები დაშტრიხე ....   ისინი შეესაბამებიან    გამოსაკვლევი გამოსახულების   დადებითობას   (>0),

ქვედა უბნის    x ები კი უარყოფითობას (<0) .

p.s.  წირის მეშვეობით უტოლობის ამოხსნის   აუცილებელი პირობაა  ა)   გამოსაკვლევი გამოსახულების წინ  + -ს არსებობა   და ბ)  ფესვთა    ნამრავლში     x -ს კოეფიციენტების დადებითობა(+)

------------------------------------------------------------------------

ჰუუუუ!!!!....   მეტი ვერ შევძელი... მომიტევე

-----------------------------------------------------------------------

ოლეგი გაბრიაძე  599-544-227

 This email address is being protected from spambots. You need JavaScript enabled to view it..........  ფიზიკა - მათემატიკა - ზოგადი

უნარები   აბიტურიენტებისათვის,

მაგისტრობისა  და მასწავლებლობის მაძიებლებისათვის.